18 Лекция 18. Методы идентификации, основанные на аппроксимации характеристик объектов и сигналов

 

Содержание лекции:

- методы сглаживания импульсной переходной функции

 

Цель лекции:

-    изучить методы непараметрической идентификации, базирующиеся на аппроксимации неизвестных динамических характеристик объекта аналитическими выражениями.

 

18.1 Метод идентификации, основанный на совместной аппроксимации импульсной переходной и корреляционных функций

Регуляризующего эффекта можно достичь за счет предварительного сглаживания корреляционных функций сигналов объекта с помощью какого-либо аппроксимирующего полинома. В соответствии с этим методом импульсная переходная функция аппроксимируется выражением (17.1), где коэффициенты (17.2). При этом правая часть системы алгебраических уравнений (16.5), эквивалентных уравнению Винера-Хопфа, также аппроксимируется теми же функциями

                                                                                      (18.1)

причем, для получения системы с числом уравнений, равным числу неизвестных, число аппроксимирующих функций N в выражениях (17.1) и (18.1) выбирается одинаковым.

В выражении (18.1) в отличие от (17.1) коэффициенты

                                                                                        (18.2)

можно считать заданными, так как значения взаимной корреляционной функции R_yx(t) в узлах заданы, а функции {φ(τ)}известны.

Подставим в систему алгебраических уравнений (16.5), эквивалентных уравнению Винера-Хопфа, выражения(17.1) для импульсной переходной функции и (18.1) для взаимной корреляционной функции; умножим обе части      на φ_j(τ) и суммируем от τ=0 до τ=m:

                  .                   (18.3)

В силу ортогонормированности функций {φ_j(τ)} приходим к системе линейных уравнений относительно неизвестных коэффициентов a_k:

                                                                                            (18.4)

где                                   (18.5)

Решив эту систему, найдем оценку импульсной переходной функции по выражению (17.1). Система уравнений (18.4) имеет существенно меньший порядок, чем исходная система, и хорошо обусловлена в силу гладкости{φ_j(τ)}и невысокого порядка. Это позволяет получать достаточно точные оценки импульсных переходных функций путем простых вычислений. В процессе решения возникают трудности, связанные с выбором количества аппроксимирующих функций, о которых упоминалось и ранее.

 

18.2 Метод идентификации, основанный на аппроксимации сигналов

Если входные и выходные сигналы объекта могут быть аппроксимированы каким-либо аналитическим выражением, импульсная переходная функция может быть получена из интеграла свертки или из уравнения Винера-Хопфа также в аналитическом виде.

Рассмотрим реализацию этого подхода. Входные и выходные сигналы объекта аппроксимируются на интервале наблюдения линейной комбинацией некоторых функций. Искомую импульсную переходную функцию также аппроксимируют этой же системой функции. Например, пусть сигналы разложены в ряды ортогональных полиномов {p_i(t)}:

                                                                            (18.6)                                          

где   ,    а pⁱ_j - коэффициенты полинома.

То есть сигналы представляются в виде степенных рядов

                                                                                   (18.7)

где коэффициенты связаны с коэффициентами разложения     соотношениями:

                               .                                                               

Импульсную переходную функцию тоже ищем в виде степенного ряда

                                                                                                (18.8)

Подставляя  (18.7)  и (18.8) в интеграл свертки, получаем

                               .                                        (18.9)

Приравнивая коэффициенты при равных степенях, получим систему алгебраических уравнений для определения коэффициентов g_i  ввыражении (18.8). В результате имеем:

    .            

  Представляет интерес аппроксимация сигналов в комплексной области, то есть представление их рядами ортогональных функций, легко преобразуемых по Лапласу. Такими функциями, являются, например, функции Лагерра L(t).  В этом случае имеем:

                                                                                       (18.10)

Соотношения (18.10) в комплексной плоскости запишутся как

                

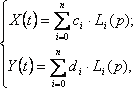
а передаточная функция объекта имеет вид:

                 .                  

Между коэффициентами {a_n} и {c_k} имеют место следующие соотношения:          

                              

Можно получить аналогичные соотношения между {b_i} и {d_i}.

Если сигнал, подаваемый на вход объекта, носит кусочно-постоянный характер или может быть аппроксимирован кусочно-постоянной функцией с достаточной степенью точности, алгоритмы идентификации упрощаются. Для j-го интервала входного сигнала с постоянным значением можно записать

                      ,  где h(t) - переходная функция.

Разложим ее по некоторой ортнормированной системе функций:

                      .                                                                                  

В этом случае, разложив выходной сигнал по той же системе функций, можно записать:

                   ,  откуда следует:    .                                                                                               

Аналогичным образом можно поступить и в том случае, если входной сигнал может быть аппроксимирован кусочно-линейной функцией.

Аппроксимирующие функции обычно выбираются таким образом, чтобы достичь хорошего приближения при небольшом их числе. Приведем некоторые полиномы, широко использующиеся при решении задач идентификации.

Исходные полиномы Лагерра ортонормальны с весомω(t) = e^-t на интервале (0, ∞). Полином Лагерра  n-го порядка имеет вид

                                ,                                                            (18.11)

а выражения для первых трех полиномов соответственно равны

                                .                                              

 Полиномы Лагерра ортогональны таким образом, что

                                 .                                                   

После нормировки выражение (18.11) примет вид:

                                 .                                                           

Другим важным типом аппроксимирующих функций являются полиномы Лежандра, ортогональные на интервале [-1,1]. n–ый полином Лежандра описывается выражением

.                                                                   Первые полиномы Лежандра, таким образом, имеют вид:

                                                          

Полиномы Чебышева ортогональны на интервале [-1,1] с весом

                                                                              

Полином Чебышева n -го порядка имеет вид:

                                                                                            

Выражения для первых полиномов:

               

А коэффициенты разложения функцииf(x) по системе полиномов Чебышева имеют вид:

                                 .                                                                      

Аппроксимация произвольной функции полиномами Чебышева позволяет добиться равномерного распределения погрешности и избежать ее накопления к концу интервала.