14 Лекция 14. Параметрическая идентификация линейных объектов

 

Содержание лекции:

-         параметрическая идентификация линейных объектов

 

Цель лекции:

-    изучить методы параметрической идентификации линейных объектов (статические и динамические детерминированные объекты).

 

Рассматриваем линейные объекты или объекты, которые с достаточной мерой приближения можно принять за линейные. В параметрическом случае модель определяется набором параметров, которые необходимо оценить в процессе идентификации. Чтобы уяснить процедуру минимизации функционала невязки, рассмотрим вначале статический детерминированный случай.

 

14.1 Статические детерминированные линейные модели

Модель линейного объекта с n входами и m выходами имеет единственную структуру и описывается системой линейных алгебраических уравнений

           

Идентифицируются m(n+1) коэффициентов c_ij, i =1,..., m; j = 0,…, n.

В векторном виде эта система имеет вид 

где   X = (x₁, x_2,,…, x_n) - вход; Y = (y₁, y_2,,…, y_n) – выход; C₀ = (c₁₀, …,c_m0);

                    

Информацию об объекте можно представить в виде {X_j, Y_j ^k}, k =1,…,m, .

Идентифицируются C₀ и C.

Рассмотрим случай n>1, m=1. Случай m>1 сводится к m-кратному повторению рассматриваемого случая.

Итак,  или 

(n+1) неизвестных коэффициента подлежат оценке на основе информации {X_j, Y_j}, j =1,…,N, где X_j=(x_1j, x_2j, …, x_nj)  - j-е состояние входа, Y_j – реакция на этот вход.

Обычный подход к решению этой задачи - приравнивание выходов объекта и модели

           ,                                                                  (14.1)

Получили N уравнений с (n+1) неизвестными (систему уравнений идентификации). Эта система имет единственное решение, если ранг матрицы

равен  (n+1).

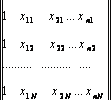                                                                                       (14.2)   

Это возможно в  том случае, если найдены (n+1) линейно-независимых строк этой матрицы. Поэтому из Nпар следует выбрать (n+1) линейно-независимую строку:

            .

В этом случае решение (14.1) определяет точное значение идентифицируемых параметров (если объект действительно линеен).

Однако при этом методе не используется вся исходная информация. Используем ее. Введем невязку:

                                                                                  (14.3)

где  - локальная невязка (на i-той паре).

Задачу оценки параметров С можно теперь представить как задачу минимизации невязки (14.3), то есть свести к системе линейных алгебраических уравнений:

                                          (14.4)

Определитель этой системы не равен нулю, если ранг (14.2) равен (n+1).

Решения систем (14.1) и (14.4) совпадают. Зачем же использовать этот более сложный метод, тем более, что (14.1) требует лишь (n+1)точку? Зачем остальныеN – (n+1) точек? Если объект действительно детерминированный и линейный, то эти точки не нужны и второй способ не стоит применять. Однако, возможно, что объект почти линеен. Тогда по двум точкам получается очень грубая модель. Второй способ как бы «спрямляет» объект.

Если же ранг системы (14.4) меньше (n+1)? В этом случае:

       1. Повторить измерения (может быть, вначале состояния системы были недостаточно разнообразны). Если опять не получится, то изменить структуру модели.

2.   Понизить число идентифицируемых параметров, то есть исключить рассмотрение одного из входов, например, того, который мало изменяется. И до тех пор, пока ранг (14.2) не совпадет с ее размерностью.