16.2 Алгебраический метод решения уравнения Винера-Хопфа
Один из методов решения уравнения (16.4) – алгебраический. Представим (16.4) в виде системы линейных алгебраических уравнений. Для этого перейдем к дискретному времени, интеграл запишем в виде суммы. Интервал разбивается на mравных интервалов t, 2t, …, mt и интегралзаписываетсяприближенно в виде суммы:
(16.5)
Обозначим gi =g(it) и полагая τ = t, 2t,..., mt, получим систему:
Rx·G=Q (16.6)
где G
= [g1,
g2,…,gm]T,
Q= [q1,
q2…,
qm]T, 
,
Rx – квадратная симметричная матрица mхm:
.
Таким образом, получили систему mлинейных уравнений для определения mзначений ординат весовой функции g(τ) в точках t, 2t,…, mt.
В
реальных объектах обычно g(0)
= 0, поэтому в правых частях уравнений
(16.6) можно убрать первые слагаемые. Кроме
того, чтобы сохранить диагональную
симметричность определителя системы,
часто 
сдвигают
на один шаг , то есть систему (16.6)
рассматривают не с первой строки, а со
второй. Если отрезок ∆
достаточно мал, ошибка будет незначительна.
Уравнение Винера-Хопфа является плохо обусловленным: даже малые вариации в исходных значениях корреляционных функций приводят к большим вариациям решений. К тому же вместо истинных значений корреляционных функций использовались их оценки. Поэтому решение уравнения Винера-Хопфа получается с большими погрешностями. Хотя полученные таким образом импульсные переходные функции имеют малую среднеквадратичную ошибку, близкую к минимуму, ценность их невелика, так как эти функции не соответствуют физическому смыслу процессов в объекте. Физический смысл имеют гладкие решения.
Один из методов регуляризации плохо обусловленных уравнений основан на том, что решение ищется в виде линейной комбинации собственных функций интегральных операторов (в случае интегральных уравнений) или собственных чисел линейных операторов (в случае систем линейных алгебраических уравнений). При решении задачи идентификации собственные функции оператора свертки, как правило, неизвестны. Однако, например, разложение решений уравнения Винера-Хопфа по некоторой системе гладких функций, соответствующих реальному протеканию процессов в идентифицируемом объекте, обладает хорошими регуляризующими свойствами. Это относится и к сглаживанию входящих в уравнение Винера-Хопфа корреляционных функций.
17 Лекция 17. Методы идентификации, основанные на
аппроксимации характеристик объектов и сигналов
Содержание лекции:
- методы сглаживания импульсной переходной функции
Цель лекции:
- изучение методов непараметрической идентификации объектов, основанные на аппроксимации неизвестных характеристик объектов и сигналов.
При практической реализации методов идентификации широко используются процедуры аппроксимации, обладающие сглаживающими свойствами.
17.1 Краткие сведения об аппроксимации функций
Задача аппроксимации – это задача приближения функции по какой-либо системе функций. Пусть рассматриваемая функция f(t) абсолютно интегрируема на интервале [0,T]. На практике это требование, обычно, выполняется. Эта функция разлагается по некоторой системе аппроксимирующих функций {φ(t)}, абсолютно интегрируемых на том же интервале времени
.
(17.1)
Вид системы аппроксимирующих функций выбирается исходя из априорной информации об аппроксимируемой функции. Коэффициенты аппроксимации выбираются таким образом, чтобы минимизировать некоторый заранее выбранный критерий приближения. Можно воспользоваться одним из следующих видов приближения: равномерным, интерполяционным, квадратичным. Для точного решения задачи с использованием двух первых видов приближения не существует конечного алгоритма для вычисления коэффициентов разложения на бесконечном интервале (который чаще всего входит в алгоритмы идентификации). Это обстоятельство, а также алгоритмическая простота реализации квадратичных приближений обусловили их широкое распространение. Коэффициенты разложения в этом случае могут быть получены из системы алгебраических уравнений. Вводя обозначения для скалярных произведений
(17.2)
получим искомую систему:
a0(φ0, φ0) + a1(φ0, φ1) + … + aN(φ0, φN) = (φ0, f);
………………………………………………… (17.3)
a0(φ0, φN) + a1(φ1, φN) + … + aN(φN, φN) = (φN, f).
Условием единственности решения системы (17.3) является неравенство нулю ее определителя. Определитель не равен нулю тогда и только тогда, когда выбранная система аппроксимирующих функций является линейно-независимой.
Если не предъявлять к аппроксимирующей системе функций больше никаких требований (кроме абсолютной интегрируемости), система (17.3) решается совместно. И при изменении длины отрезка N нужно заново вычислять все коэффициенты an. Кроме того, для решения системы надо определить N(N+1)/2 интегралов вида (17.2). Для достижения независимости определения коэффициентов аппроксимации an и упрощения решения системы (17.3) функции {φ(t)} целесообразно выбрать ортогональными на интервале [0,T], то есть удовлетворяющими условию
(17.4)
где cn - некоторая постоянная.
Если функции {φ(t)} ортогональны, определитель системы (17.3) становится диагональным и формулы для вычисления коэффициентов упрощаются до вида
.
Если постоянныеcn=1, система функций {φ(t)} является ортонормированной, выражения для формул упрощаются до вида широко известных формул Фурье, а сами коэффициенты в этом случае называются коэффициентами Фурье (по аналогии с рядом Фурье, члены которого также представляют собой ортонормированные на [0,T] функции. Иногда выбирают функции, ортогональные с некоторым весом w(t)
.
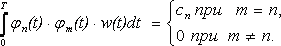(17.5)
Функция веса выбирается таким образом, чтобы выделить ошибку на интересующем интервале изменения независимой переменной.
Недостатком рассмотренного выше алгебраического метода является необходимость решения системы Винера-Хопфа.Некорректность исходного интегрального уравнения приводит к плохой обусловленности этой системы. Есть несколько способов получения плавной импульсной переходной функции, которые выбираются на основе имеющейся априорной информации об объекте.