Энергетические характеристики молекулы водорода

Располагая выражениями для волновых функций, можно вычислить энергию молекулы в каждом из трех возможных состояний по стандартной формуле: Е=_ Ф*НФdv. Для этого нужно знать явный вид оператора Гамильтона, который для молекулы водорода имеет вид:

Н = Н_a + H_b + H_ab

где Н_aиН_b— операторы Гамильтона для отдельных атомов водорода, содержащих электроны № 1 и № 2, соответственно.

Н_a = (–²/2m₁)₁² – e²/r_1a и Н_b = (–²/2m₂)₂² – e²/r_2b

Оператор Н_abсодержит члены, описывающие взаимодействие между атомами (энергии притяжения электронов к "чужим" ядрам (1aи2b), а также энергии межэлектронного и межъядерного отталкивания) и относится сразу к обоим атомам.

Н_ab = – e²/r_1b – e²/r_2а + е²/r₁₂ + e²/r_ab

Рассмотрим для примера волновую функцию основного состояния

Ф = D₁(АВ + ВА) + D₂(AA + BB).

Вклад ионных РФ существенно меньше, чем ковалентных (D₂ <<D₁). Поэтому, в первом приближении, можно ограничиться учетом только ковалентных форм и взять приближенное выражение для волновой функции:

Ф  D(АВ + ВА).

Вначале найдем величину коэффициента D. Это можно сделать из условия нормировки.

_ Ф*Ф dv = D ² _ (AB + BA)*(AB + BA) dv = D² [ _{ (}A*B*  AB) dv +

+ _{ (}A*B*  BA) dv + _{ (}B*A*  AB) dv + _{ (}B*A*  BA) dv ] = 1

В этом выражении имеется четыре интеграла. Рассмотрим первый из них. В подынтегральном выражении два сомножителя относятся к первому электрону, а два — ко второму. Такие интегралы можно представить в виде произведения более простых интегралов, каждый из которых включает только координаты только первого или только второго электрона. В результате шестимерный интеграл распадается на два трехмерных, каждый из которых представляет собой стандартное условие нормировки для атомных орбиталей. Поскольку атомные орбитали АиВнормированы, оба интеграла-сомножителя оказываются равными 1.

_(A*B*  AB) dv = _ [A*₍₁₎A₍₁₎  B*₍₂₎B₍₂₎ dv₁  dv₂ =

= _ A*₍₁₎A₍₁₎ dv₁  _ B*₍₂₎B₍₂₎ dv₂ = 1  1 = 1

Проанализируем второй интеграл:

_(A*B*  BA) dv = _ [A*₍₁₎B₍₁₎  B*₍₂₎A₍₂₎ dv₁  dv₂ =

= _ A*₍₁₎B₍₁₎ dv₁  _ B*₍₂₎A₍₂₎ dv₂ = s  s = s ²

Трехмерные интегралы-сомножители (s) в этом выражении называютсяинтегралами перекрывания. Величина такого интеграла определяется величиной области перекрывания, в которой обе атомные орбитали (АиВ) заметно отличаются от нуля.

Очевидно, что s0, когда ядрааиbудаляются друг от друга, иs1, когда ядра сближаются.

Третий интеграл построен точно так же, как и второй, а четвертый — так же, как первый. В итоге выражение для нормировки приобретает вид:

_ Ф*Ф dv = D² [ 1 + s ² + s ² + 1] = 1

Отсюда получаем для нормировочного множителя и волновой функции:

D = 1/(2 + 2s ²)^1/2 и Ф  (АВ + ВА)/(2 + 2s ²)^1/2

Подставим это выражение в формулу для вычисления энергии:

Е = _ Ф*НФ dv = [1/(2 + 2s ²)] _ (АВ + ВА)*Н(АВ + ВА) dv

Раскрыв скобки в подынтегральном выражении, получим вместо одного сложного интеграла четыре более простых.

_ (АВ + ВА)*Н(АВ + ВА) dv = _ (АВ)*Н(АВ) dv + _ (АВ)*Н(ВА) dv +

+ _ (ВА)*Н(АВ) dv + _ (ВА)*Н(ВА) dv = I + II + III + IV

Проанализируем эти интегралы. Для начала можно отметить, что по структуре интегралы попарно равны друг другу: I=IVиII=III, и поэтому достаточно детально рассмотреть только два из них, напримерIиII.

Подставляя в интеграл Iвыражение для гамильтониана, получим сумму трех еще более простых интегралов:

_ (АВ)*Н(АВ) dv = _ (АВ)* (Н_a + H_b + H_ab) (АВ) dv =

_{= } (АВ)*(Н_a)(АВ) dv + _ (АВ)*(Н_b)(АВ) dv + _ (АВ)*(Н_ab)(АВ) dv

Оператор Гамильтона в первом интеграле действует только на волновые функции типа А. Волновые функции типаВдля оператораН_авыступают как простые числовые множители и их можно выносить за знак оператора. Это дает возможность разбить первый из трех интегралов в произведение двух трехмерных интегралов-сомножителей:

_ (АВ)*(Н_а)(АВ) dv = _ В*B dv_b  _ А*(Н_а)А dv_a

Первый сомножитель представляет собой условие нормировки для атомной орбитали Ви поэтому равен 1. Второй сомножитель представляет собой энергию, которую имеет электрон, принадлежащий атому водорода с ядрома(Е_Нa) и находящийся в состоянииА. Второй интеграл построен аналогично первому и равен энергии, которую имеет электрон, принадлежащий атому водорода с ядромb(Е_Нb) и находящийся в состоянииВ.

Наконец, третий интеграл содержит гамильтониан, описывающий оба электрона сразу. Поэтому этот интеграл нельзя разложить в произведение двух одноэлектронных и его нужно рассматривать как некоторую энергию, характеризующую взаимодействие двух атомов водорода. Эта энергия называется кулоновским интегралом(J_ab), который можно представить и в более детальной записи:

_ (АВ)*(Н_ab)(АВ) dv = _ (АВ)*(– e²/r_1b – e²/r_2а + е²/r₁₂ + e²/r_ab)(АВ) dv =

_{= } (АВ)*(– e²/r_1b)(АВ) dv + _ (АВ)*(– e²/r_2а)(АВ) dv +

+ _ (АВ)*(е²/r₁₂)(АВ) dv + _ (АВ)*(e²/r_ab)(АВ) dv =

_{= } (В*B)dv₂  _{ A*}(– e²/r_1b)(А) dv₁ + _ (A*A)dv₁  _{ B*}(– e²/r_1b)(B) dv₂ +

+ _ (АВ)*(е²/r₁₂)(АВ) dv + (e²/r_ab)_ (А*A)dv₁  _ (B*В) dv₂ =

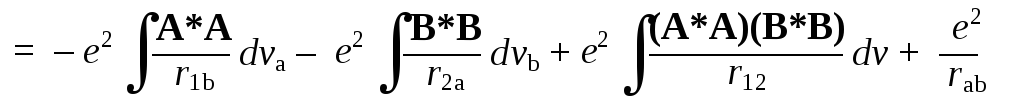
Произведение e(A*A)dv_aпредставляет собой электрический зарядdq_a, локализованный в малом объемеdv_a, принадлежащем атому Н_а. Произведениеdq_ae/r_1b, стоящее под знаком первого интеграла, — это потенциальная энергия взаимодействия заряженного объемаdv_aэлектронного облака, созданного электроном № 1 с ядром атома Н_b. Поэтому первый интеграл представляет собой полную энергию кулоновского притяжения электрона № 1, расположенного на орбиталиA, к ядруb; второй — энергию кулоновского притяжения электрона, расположенного на орбиталиB, к ядруa; третий — энергию кулоновского отталкивания двух электронных облаков, а четвертый — энергию кулоновского отталкивания двух ядер. Кулоновский интеграл, следовательно, отражает все электростатические взаимодействия между составными частями двух атомов, ядра которых сближены на расстояниеr_ab. Таким образом, для интегралаIполучаем следующую оценку:

I = Е_Нa + Е_Нb + J_ab = 2E_H + J

Перейдем к анализу интеграла II. Подставляя в этот интеграл выражение для гамильтониана, получим, как и в предыдущем случае, сумму трех простых интегралов:

_ (АВ)*Н(ВА) dv = _ (АВ)* (Н_a + H_b + H_ab) (ВА) dv =

_{= } (АВ)*(Н_a)(ВА) dv + _ (АВ)*(Н_b)(ВА) dv + _ (АВ)*(Н_ab)(ВА) dv

Первый из этих интегралов может быть разложен в произведение двух одноэлектронных:

_ (АВ)*(Н_a)(ВА) dv = _ В*А dv_b  _ А*(Н_a)В dv_a

Первый сомножитель в этом выражении представляет собой интеграл перекрывания (s). Второй сомножитель можно преобразовать с учетом того, что гамильтониан являетсясамосопряженнымоператором, для которых выполняется правило:

_ А*НВ dv = _ В*Н*А dv

Атомная орбиталь А является собственной функцией для оператораН_aи для нее выполняется соотношение:

Н_AА = Н_A*А = Е_На  А

Следовательно,

_ А*(Н_a)В dv_a = _ В*Н_a*А dv_a = _ В*Е_НаА dv_a =

= Е_На  _ В*А dv_1a = Е_На  s

С учетом первого множителя получаем величину Е_Наs². Второй интеграл устроен аналогично первому и поэтому равенЕ_Нbs².

Третий интеграл не поддается разложению на одноэлектронные сомножители и должен рассматриваться как характеристика межатомного взаимодействия. Этот интеграл называется обменным(K_ab). Его, как и кулоновский, можно представить в более детальной записи:

_ (АВ)*(Н_ab)(ВA) dv = _ (АВ)*(– e²/r_1b – e²/r_2а + е²/r₁₂ + e²/r_ab)(ВA) dv =

_{= } (АВ)*(– e²/r_1b)(ВA) dv + _ (АВ)*(– e²/r_2а)(ВA) dv +

+ _ (АВ)*(е²/r₁₂)(ВA) dv + _ (АВ)*(e²/r_ab)(ВA) dv =

_{= } (В*A)dv₂  _{ A*}(– e²/r_1b)(B) dv₁ + _ (A*B)dv₁  _{ B*}(– e²/r_1b)(A) dv₂ +

+ _ (АВ)*(е²/r₁₂)(ВA) dv + (e²/r_ab)_ (А*B)dv₁  _ (B*A) dv₂ =

Из формы интегралов в этом выражении видно, что они представляют собой особые кулоновские поправки к полной энергии молекулы. Они возникают вследствие того, что в области перекрывания плотность электронного облака молекулы не равна сумме плотностей двух исходных атомных электронных облаков. К этой сумме добавляется интерференционный вклад. Другими словами, в области перекрывания возникают два дополнительных электрических заряда (от каждого электрона), равные es(A*B)dv₁, которые взаимодействуют и с ядрами молекулы, и между собой.

Можно сказать, что кулоновский интеграл ( J ) вычисляется в предположении, что сферически симметричная форма электронных облаков атомов (АиВ) при их вхождении в состав молекулы не изменилась. В действительности (вследствие интерференции в области перекрывания) оба эти облака деформированы:АА'иBB'. В результате энергия межатомных кулоновских взаимодействий оказалась вычисленной неправильно. Обменный интеграл представляет собой необходимую поправку.

В итоге получаем следующую оценку интеграла II:

II = Е_На  s² + Е_Нb  s² + K = 2 E_H  s² + K

Теперь, с учетом равенств I=IVиII=III, запишем полное выражение для энергии молекулы:

E_g = (I + II + III + IV)/(2 + 2s²) = (2 E_H + J + 2 E_H  s² + K +

+ 2 E_H  s² + K + 2 E_H + J )/(2 + 2s²) =

= [4E_H (1 + s²) + 2 (J + K)]/2(1 + s²) = 2 E_H + (J + K)/(1 + s²)

Таким образом, энергия молекулы водорода представлена в виде суммы двух вкладов: 1) энергии двух атомов, из которых молекула образовалась, и 2) поправки на энергию межатомных взаимодействий. Из формулы видно, что эта поправка состоит из двух частей — кулоновскойиобменной. Их величины можно вычислить, зная явный вид орбиталейАиВ.

Следует подчеркнуть, что найденное выражение для энергии носит общий характер в методе ВС. Независимо от размера молекулы, энергия всегда представляется в виде суммы энергий изолированных атомов, из которых молекула образована, и поправок (кулоновских и обменных) на межатомные взаимодействия.

Аналогичные вычисления можно выполнить и для других состояний. Например, для триплетного возбужденного состояния с волновой функцией Ф_uполучим:

E_u = 2 E_H + (J – K)/(1 – s²)

Нужно иметь в виду, что значение кулоновского интеграла положительно, а обменного — отрицательно. Поэтому энергия триплетного состояния выше, чем основного (E_u>E_g).