Вычисление энергии в методе мо

Располагая явным видом глобальных волновых функций, можно вычислить полную энергию любого из шести возможных состояний молекулы. Энергия может иметь всего четыре значения, т.к. в нерелятивистском приближении она определяется только формой пространственного множителя. Следовательно, три состояния, образующие триплет, будут вырождены по энергии. Рассмотрим процедуру вычисления энергии на примере состояния Ф₁. Оператор Гамильтона в методе МО состоит из тех же самых слагаемых, что и в методе ВС, которые, однако, группируются иначе — не "по атомам", а "по электронам":

Н = Н₁ + H₂ + H₁₂

где Н₁иН₂— операторы Гамильтона для электронов № 1 и № 2, соответственно, имеющие вид:

Н₁ = (–²/2m₁)₁² – e²/r_1a – e²/r_1b и Н₂ = (–²/2m₂)₂² – e²/r_2a – e²/r_2b

Эти операторы отражают наличие у каждого электрона кинетической энергии и двух слагаемых потенциальной энергии, определяемых кулоновским притяжением электрона к двум ядрам молекулы.

Двухэлектронный оператор Н₁₂содержит члены (в данном случае — всего один), характеризующие взаимодействие между электронами.

Н₁₂ = е²/r₁₂

Следует обратить внимание на то, что в методе МО энергию отталкивания ядер обычно не включают в гамильтониан, так как она не зависит от координат электронов и способа их движения.

Пространственная часть волновой функции Ф₁имеет вид (без учета нормировочного множителя):Ф₁=GG. Тогда выражение для энергии получим в следующем виде:

_{Е = } (GG)*Н(GG) dv = _ (GG)* (Н₁ + H₂ + H₁₂) (GG) dv =

_{= } (GG)*(Н₁)(GG) dv + _ (GG)*(Н₂)(GG) dv + _ (GG)*(Н₁₂)(GG) dv

Первый из этих интегралов может быть разложен в произведение:

_ (GG)*(Н₁)(GG) dv = _ G*₍₂₎G₍₂₎ dv₂  _ G₍₁₎*(Н₁)G₍₁₎ dv₁

Первый сомножитель в этом выражении представляет собой условие нормировки для МО типа Gи поэтому равен 1. Второй интеграл-сомножитель представляет собой энергию электрона № 1, заселяющего МО типаGв отсутствие остальных электронов. Такая величина обычно называетсяорбитальной энергией ():

_G = _ G₍₁₎*(Н₁)G₍₁₎ dv₁

Второй двухэлектронный интеграл также может быть разложен в произведение двух одноэлектронных:

_ (GG)*(Н₂)(GG) dv = _ G*₍₁₎G₍₁₎ dv₁  _ G₍₂₎*(Н₂)G₍₂₎ dv₂

Он, очевидно, равен орбитальной энергии электрона № 2, которая имеет ту же самую величину, что и для электрона № 1.

Наконец, третий двухэлектронный интеграл не разлагается в произведение одноэлектронных сомножителей и должен быть вычислен непосредственно. Он представляет собой энергию кулоновского отталкивания двух одинаковых электронных облаков типа G(одно для электрона № 1, а второе для электрона № 2) и называетсякулоновским интегралом(J). В итоге получаем следующую оценку полной энергии молекулы:

Е_GG = _G + _G + J_GG

В отличие от метода ВС, где энергия представляется в виде суммы вкладов атомов и поправок на межатомные взаимодействия, в методе МО глобальная энергия молекулы складывается из вкладов отдельных электронов и поправок на межэлектронные взаимодействия.

Вычислим энергию триплетного состояния Ф_u=GU – UG.

_{Е = (1/2) } (GU – UG)*Н(GU – UG) dv =

_{(1/2)[ } (GU)*Н (GU) dv – _ (GU)*Н (UG) dv – _ (UG)*Н (GU) dv +

+ _ (UG)*Н (UG) dv ] = I – II – III + IV

Проанализируем интеграл I. С учетом структуры гамильтониана этот интеграл распадается в сумму трех более простых интегралов.

I _{= } (GU)*(Н)(GU) dv = _ (GU)*(Н₁)(GU) dv + _ (GU)*(Н₂)(GU) dv +

+ _ (GU)*(Н₁₂)(GU) dv = 1 + 2 + 3

Первый из них содержит одноэлектронный гамильтониан и поэтому его можно разложить в произведение двух одноэлектронных интегралов:

_{1 = } (U*U)dv₂  _{ G*}Н₁Gdv₁

Первый сомножитель равен 1, т.к. используется нормированная функция U. Второй сомножитель представляет собой орбитальную энергию_G. Второй интеграл устроен аналогично:

_{1 = } (G*G)dv₁  _{ U*}Н₁Udv₂ = _U

Третий интеграл — кулоновская поправка J_GU. Итого получим:

I=_G+_U +J_GU.

Проанализируем интеграл II. С учетом структуры гамильтониана этот интеграл распадается в сумму трех более простых интегралов.

II _{= } (GU)*(Н)(GU) dv = _ (GU)*(Н₁)(UG) dv + _ (GU)*(Н₂)(UG) dv +

+ _ (GU)*(Н₁₂)(UG) dv = 1 + 2 + 3

Первый из них содержит одноэлектронный гамильтониан и поэтому его можно разложить в произведение двух одноэлектронных интегралов:

_{1 = } (U*G)dv₂  _{ G*}Н₁Udv₁

Первый сомножитель равен 0, так как разные МО ортогональны друг другу. Следовательно и весь интеграл 1 равен нулю. Интеграл 2 устроен аналогично и также равен 0. Интеграл 3 называется обменным: 3 =K_GU. Итого получим:II= –K_GU. Наконец, заметим, что в силу симметрии молекулы имеют место равенства:I=IVиII=III. Следовательно, полная энергия нечетного состояния равна:E_u=_G+_U+J_GU–K_GU.

Аналогично можно вычислить энергии двух оставшихся состояний и установить качественный вид энергетической диаграммы:

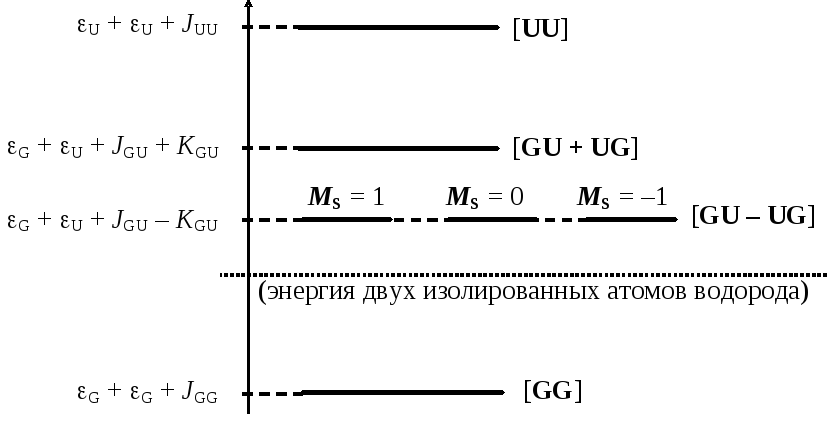
Следует обратить внимание на то, что в тех случаях, когда электроны заселяют разные МО (в данном случае GиU), в выражении для энергии появляется дополнительная поправка —обменный интегралK. (Несмотря на одинаковые названия, кулоновские и обменные интегралыJиKв методах ВС и МО имеют различные числовые значения и разный физический смысл: в методе ВС они являютсямежатомнымипоправками, а в методе МО —межэлектронными.)