4.2 Властивості бінарних відношень

Бінарні відношення мають три основні властивості, відповідно до яких вони класифікуються: рефлексивність, симетричність, транзитивність.

Визначення 4.6. Бінарне відношення є рефлексивним, якщо виконується умова:

, (4.5)

тобто для будь-якого елемента з множини кожна впорядкована пара вигляду належить бінарному відношенню.

У матриці рефлексивного бінарного відношення на головній діагоналі розташовані одиниці:

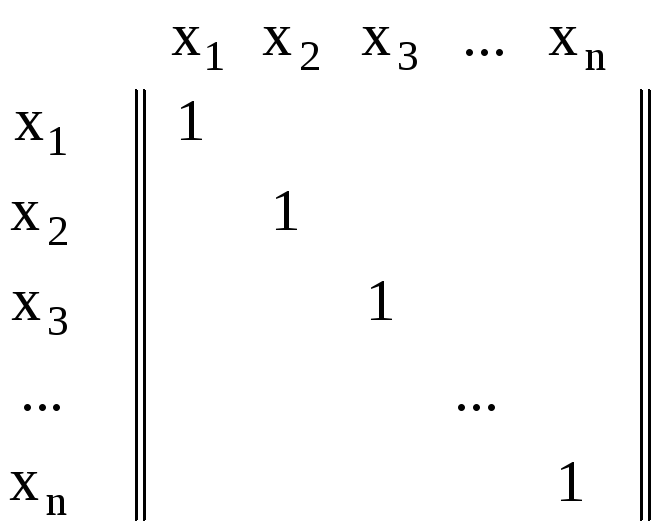, (4.6)

уграфі – всі вершини мають петлі (рис. 4.3):

Рисунок 4.3 – Петля в графі рефлексивного бінарного відношення

Визначення 4.7. Бінарне відношення є симетричним, якщо виконується умова:

, (4.7)

тобто для будь-яких елементів , з множини таких, що впорядкована пара належить бінарному відношенню , симетрична пара також належить даному відношенню.

Матриця симетричного бінарного відношення симетрична відносно головної діагоналі:

. (4.8)

У графі симетричного бінарного відношення – наявність між кожною парою вершин, що перебувають у відношенні , двох протилежно спрямованих дуг (рис. 4.4):

Рисунок 4.4 – Симетрично спрямовані дуги

Приклад 4.5. Видалення в графі із прикладу 4.3 (див. рис. 4.2) дуг , , , призводить до симетричного відношення (рис. 4.5).

Рисунок 4.5 – Симетричне бінарне відношення

Визначення 4.8. Бінарне відношення називається транзитивним, якщо виконано властивість:

, (4.9)

для будь-яких трьох елементів таких, що послідовно утворені впорядковані пари із цих елементів , перебувають у відношенні , тоді пари із крайніх елементів також належать даному відношенню.

Граф транзитивного бінарного відношення характеризується наявністю транзитивно замикаючих дуг (рис. 4.6) для кожних двох пар з умови (посилки) даної властивості (4.9).

Р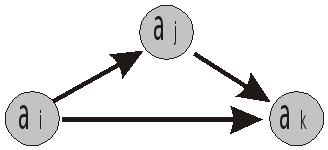исунок 4.6 – Транзитивно замикаюча дуга

Приклад 4.6. У графі на рис. 4.5 транзитивно замикаючими є такі дуги: для впорядкованих пар , – ; для пар , – ; для пар , – ; для , – .

Вводяться також додаткові властивості, засновані на наведених вище:

– антирефлексивність (у матриці суміжності на головній діагоналі всі елементи нульові, у графі не існує петель): ;

– нерефлексивність (у матриці суміжності по головній діагоналі розташовані як нулі, так і одиниці, у графі деякі вершини мають петлі): ;

– антисиметричність (всі відповідні симетричні комірки матриці суміжності різні; у графі немає жодної пари симетрично спрямованих дуг): ;

– несиметричність (якщо умова симетричності порушується хоча б для однієї пари, тобто ;

– нетранзитивність: якщо , для яких не виконується умова транзитивності, тобто .

Приклад 4.7. Після видалення симетричних і транзитивно замикаючих дуг у графі із прикладу 4.3 (див. рис. 4.2), тобто всіх дуг, крім , відношення стає антисиметричним, антирефлексивним, не транзитивним (рис. 4.7):

Рисунок 4.7 – Антирефлексивне, антисиметричне, нетранзитивне відношення

4.3 Бінарне відношення еквівалентності

Відношення еквівалентності – спеціальний тип бінарного відношення, затребуваний на практиці.

Визначення 4.9. Бінарним відношенням еквівалентності називається рефлексивне, симетричне й транзитивне відношення, тобто :

1) рефлексивність означає, що кожний елемент еквівалентний сам собі: ;

2) симетричність означає, що якщо елемент еквівалентний елементу , то й еквівалентний елементу : ;

3) транзитивність: якщо елемент еквівалентний елементу , а еквівалентний елементу , то еквівалентний : .

Відношення еквівалентності ілюструється графом з петлями й симетрично спрямованими дугами, які попарно мають транзитивно замикаючі дуги (рис. 4.8).

Рисунок 4.8 – Граф бінарного відношення еквівалентності

Приклад 4.8. Бінарне відношення еквівалентності ілюструє роботу тригера, граф переходів якого зображений на рис. 4.10.

а б

Рисунок 4.9 – Граф переходів (а) і структура тригера (б)

Визначення 4.10. Клас еквівалентності елемента є множина всіх елементів , кожний з яких перебуває з елементом у відношенні еквівалентності:

або . (4.10)

Визначення 4.11. Розбивкою множини називається сімейство непустих попарно непересічних підмножин (класів), об'єднання яких співпадає з , тобто зображення множини у вигляді попарно непересічних підмножин називається розбивкою множини . Індекс розбивки визначається його потужністю.

Нехай – сімейство підмножин множини : . Відповідно до визначення 4.11, є розбивкою множини , якщо воно задовольняє властивості:

1) будь-яка множина із не є порожньою, тобто ;

2) довільні дві множини з розбивки не мають спільних елементів:

;

3) об'єднання всіх множин із співпадає з множиною :

.

Приклад 4.9. Розбивками триелементної множини є:

–найбільша (максимальна) розбивка індексу одиниця, що містить одну єдину непусту множину, яка співпадає з множиною ;

; ; – розбивки індексу 2;

–найдрібніша (мінімальна) розбивка, що складається з одноелементних підмножин множини , індекс розбивки дорівнює 3.

Приклад 4.10. Максимальна розбивка індексу 1 завжди містить одну єдину множину , на якій воно розглядається: – тут усього один клас, він еквівалентний U.

Приклад 4.11. Множина всіх одноелементних підмножин становить найдрібнішу розбивку, індекс якої співпадає з потужністю вихідної множини: .

Розглянемо схему розбивки множини на класи еквівалентності. Нехай на кінцевій множині задане відношення еквівалентності . Здійснимо таку побудову:

– виберемо елемент і утворимо підмножину (клас) , що складається з елемента та всіх елементів, еквівалентних йому:

;

– виберемо елемент , і утворимо підмножину (клас еквівалентності) елемента , що складається з і всіх елементів, еквівалентних йому:

; і т.п.

У результаті такої побудови породжується система класів така, що будь-який елемент із множини входить хоча б в один клас, тобто .

Дана система має такі властивості:

1) утворює розбивку, тобто класи попарно не перетинаються: ;

2) будь-які два елементи з одного класу еквівалентні: ;

3) будь-які два елементи з різних класів не еквівалентні:

.

Побудована розбивка (система класів) називається системою класів еквівалентності за відношенням .

Класи еквівалентності мають такі властивості:

1) елемент належить своєму класу еквівалентності: .

2) якщо елемент належить класу еквівалентності елемента , то класи еквівалентності елементів і співпадають: .

3) якщо класи еквівалентності перетинаються, то вони співпадають:

;

нерівні (різні) класи еквівалентності не перетинаються:

.

Таким чином, класи еквівалентності або не перетинаються, або співпадають: .

4) об'єднанням класів еквівалентності є вся множина : .

Отже, класи еквівалентності утворюють розбивку множини. Матрицю бінарного відношення еквівалентності можна зобразити у блоково-діагональному вигляді (рис. 4.10), де кожна підматриця, що складається з одиниць, відповідає класу еквівалентності.

Рисунок 4.10 – Матриця бінарного відношення еквівалентності

З формальної точки зору модель є фактор-множина елементів об'єкта, що моделюється, щодо деякого відношення еквівалентності, заданого на вихідній системі. Поняття “відношення еквівалентності”, “ фактор-множина”, “класи еквівалентності” використовуються при побудові математичної моделі деякої реально функціонуючої складної системи. Під час дослідження виникає завдання вибору істотних властивостей, деталей, ознак об'єкта, який моделюється. Відношення еквівалентності, з одного боку, ототожнює другорядні, несуттєві ознаки й властивості, з іншого боку – виділяє як представників класів еквівалентності основні властивості.