12.2 Числовий спосіб зображення булевих функцій

Числовий спосіб використовується для спрощення зображення функцій алгебри логіки. Він ґрунтується на зв’язку двійкової й десяткової систем числення. Оскільки номерами двійкових наборів є їхні десяткові еквіваленти, у числовому способі можна перераховувати тільки ті набори, де функція приймає одиничні значення, тобто замість повного перерахування термів вказуються десяткові еквіваленти (порядкові номери) двійкових наборів, на яких функція приймає значення 1, що дійсно спрощує форму запису.

Приклад 12.2. Функції з таблиці істинності в прикладі 12.1 відповідає числове подання або . В останньому записі передбачається залежність функції від трьох змінних.

12.3 Аналітична форма запису булевих функцій

За таблицею істинності можна одержати аналітичну форму запису, наприклад, ДДНФ або ДКНФ, а потім за необхідності спростити їх до ДНФ і КНФ.

Приклад 12.3. Відновити аналітичну форму функції за таблицею істинності із прикладу 12.1.

Розв’язок. ДДНФ виписується за одиничним значенням функції, які досягаються на наборах 0, 3 і 4:

,

а ДКНФ – за нульовим значенням, яким відповідають всі інші двійкові набори:

.

Отриману ДДНФ можна спростити шляхом склеювання крайніх кон’юнктивних термів, які відрізняються тільки за першою координатою. Отримана в результаті скорочена ДНФ буде такою:

.

ДКНФ також підлягає скороченню шляхом склеювання кон’юнктивних термів, що відрізняються тільки за однією координатою:

.

Таким чином, будь-яка булева функція може бути відновлена з таблиці істинності й зображена у вигляді ДДНФ, ДКНФ, а також ДНФ, КНФ. ДНФ і КНФ є скорочені форми запису ДДНФ і ДКНФ.

12.4 Геометрична інтерпретація булевих функцій

Геометричний спосіб подання булевих функцій використовується для інтерпретації перетворень над логічними виразами.

Наприклад, булеву функцію від двох змінних зображують на площині наступним чином. На рис. 12.1, б, вершини одиничного квадрата позначені довільними змінними. які утворюють кон’юнктивні терми на кожному двійковому наборі. Сусідні терми, що відрізняються тільки за однією координатою, склеюються уздовж з’єднуючого їх ребра, у результаті чого ребра позначаються спільною для вершин координатою.

аб

Рисунок 12.1 – Геометрична інтерпретація довільної булевої функції від двох змінних: а – розташування двійкових наборів; б – позначення вершин і ребер

Для функції трьох змінних геометричне зображення виконують у вигляді куба, де вершини також позначаються десятковими цифрами, двійковими цифрами, довільними змінними. При цьому ребра куба поглинають вершини, а грані поглинають ребра (рис. 12.2).

Рисунок 12.2 – Склеювання вершин і ребер одиничного куба при геометричному зображенні булевої функції від трьох змінних

При геометричному зображенні булевої функції точками позначаються вершини, у яких дана функція приймає одиничні значення.

Приклад 12.4. Побудувати графік булевої функції .

Р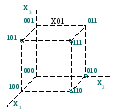озв’язок. Щоб подати дану функцію геометрично, слід відмітити вершини куба з номерами 2,5,6 і 7, на яких досягаються одиничні значення функції (рис. 12.3).

Рисунок 12.3 – Геометрична інтерпретація функції

У геометричному змісті кожний двійковий набір може розглядатися як n-мірний двійковий вектор, що визначає точку n-мірного простору. Множина наборів, на яких визначена функція, подається у вигляді вершин n-мірного куба.