10.3 Складність зображення булевих функцій

Визначення 10.8.Складність форми функціїє число букв, що входять до. Оцінка складності функції за Kвайном є, де– число кон’юктивних термів функції.

Зменшити функцію або її складність можна за допомогою законів булевої алгебри.

Приклад 10.4. Функція подана таблицею істинності:

Формула, якою вона задається, може мати вигляд ДДНФ або ДКНФ:

,

.

Складність функції є . Оцінка складності за Квайном є .

Отримані форми можна спростити до ДНФ і КНФ відповідно шляхом застосування дистрибутивного закону або закону склеювання для трьох змінних (якщо терми відрізняються тільки за однією змінною, вони підлягають склеюванню):

,

.

10.4 Теорема Шенона про розкладання булевих функцій

Теорема Шенона. Будь-яка булева функціяможе бути зображеною у вигляді розкладання Шеннона зазмінними:

(10.6)

де , , – первинні терми.

Наслідок. Граничне розкладання Шеннона прибулевої функціїмає вигляд

(10.7)

і є ДДНФ функції .

Теорема Шеннона є справедлива й у кон’юнктивній формі:

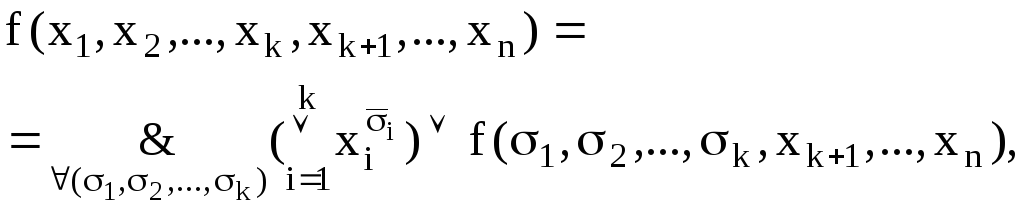(10.8)

які в межі при є ДКНФ функції:

. (10.9)

10.5 Контрольні запитання

1. Як визначається первинний терм?

2. Що являє собою елементарна кон’юнкція?

3. Що називається ДНФ функції?

4. Що таке елементарна диз’юнкція?

5. Що таке КНФ?

6. Як визначається ДДНФ?

7. Чим відрізняються ДНФ і КНФ?

8. Чим відрізняються ДНФ і СДНФ?

9. Як визначається ДКНФ?

10. Чим відрізняються КНФ і СКНФ?

11. Як складається ДДНФ за таблицею істинності?

12. Як можна одержати ДКНФ за таблицею істинності?

13. Як визначається складність формули?

14. Як визначається оцінка складності за Квайном?

15. Що являє собою розкладання Шеннона?

16. Що таке граничне розкладання Шеннона?

11 Елементи логічних схем. Булеві функції від двох змінних

Розглядаються основні властивості, фізичний зміст і схемотехнічне зображення булевих функцій від двох змінних для застосування їх при синтезі логічних схем.

11.1 Фізичний зміст логічних функцій і, або, ні та їх схемотехнічне зображення

Розглядається простий бінарний елемент – вимикач, що має два стани. Якщо даний вимикач контролюється вхідною змінною , то він виключений (розімкнутий) прита включений (замкнений) при, як показано на рис.11.1:

Рисунок 11.1 – Два стани вимикача

Можна використовувати наступне графічне позначення для зображення таких вимикачів (рис. 11.2):

Рисунок 11.2 – Графічне зображення вимикача

Можливі варіанти з'єднання лампи із джерелом живлення, наведені такими схемами (рис. 11.3):

БатареяЛампа

а

Джерело живлення Лампа

б

Рисунок 11.3 – Лампа, керована вимикачем: а – просте з'єднання з батареєю;

б – використання заземлення

Використовуючи умовне позначення , можна описувати стан лампи як функції вхідної змінної.

Якщо лампа горить, то . Якщо лампа не світиться, то.

Оскільки при, іпри, то можна стверджувати, що– логічна функція, де– логічна змінна. Це простий логічний вираз описує вихід як функцію від входу.

Розглянемо тепер можливість використання двох вимикачів для керування станом лампи, що схемотехнічно відповідає логічним функціям від двох змінних.

Нехай і– керуючі змінні (входи) для цих вимикачів.

Вимикачі можуть бути з’єднані послідовно або паралельно, як показано на рис. 11.4.

а

б

Рисунок 11.4 – Дві основні функції: а – послідовне з’єднання (функція логічного множення AND); б – паралельне з’єднання (функція логічного додавання OR)

Послідовне з’єднання вимикачів.При послідовному з’єднанні лампа світитиметься тільки тоді, якщообидвавимикачі включені (одночасно). Ця поведінка може бути описана логічним виразом:

,

де при,приабо, або.

Символ кон’юнкції називається при цьому AND-оператором.

Говорять, що схема на рис. 11.4,а реалізує логічну AND-функцію(логічне множення).

Паралельне з’єднання вимикачів.При паралельному з'єднанні двох вимикачів лампа горітиме, якщо вимикачіабовключені. Лампа також горітиме, якщообидвавимикачі включені одночасно. Лампа не горітиме в єдиному випадку, якщо обидва вимикачі розімкнуті.

Ця ситуація може бути описана як функція логічного додавання , деприабо, а також;при.

Символ диз’юнкції називається OR-оператором.

Схема на рис. 11.4,б реалізує логічну OR-функцію (логічне додавання).

У наведених вище виразах AND- і OR-оператори реалізують результат (вихід) − логічну функцію із двома вхідними змінними.

AND і OR є двома найбільш важливими логічними функціями. Разом з деякими іншими простими функціями вони можуть бути використані як складові частини (будівельні блоки) для реалізації логічних схем.

Наприклад, на рис. 11.5 показано, як три вимикачі можуть бути використані для керування лампою. Таке послідовно-паралельне з’єднання вимикачів реалізує логічну функцію .

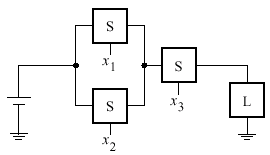
Рисунок 11.5 – Послідовно-паралельне з’єднання вимикачів

У цьому випадку лампа горить, якщо й одночасно або .

Інвертор.Для унарної операції інверсія, якій відповідає функція з однойменною назвою, схемотехнічне зображення описується схемою, як показано на рис. 11.6:

Рисунок 11.6 – Схема, що інвертує

У цьому випадку вимикач з’єднується в паралель із лампою. Лампа горітиме, коли вимикач розімкнутий.

Формально така функціональна поведінка виражається як , депри, іпри.

Значення цієї функції є зворотним до значення вхідної змінної.

Поряд з використанням терміна інверсіяможна застосовувати узагальнений терміндоповнення (як у теорії множин). Таким чином,є доповнення. У термінах операторів це є NOT-Оператор.