1.7. Дискретизация аналогового сигнала. Идеальные выборки

и z-преобразование.

Пример реализации биквада с использованием концепции переключаемых конденсаторов (ПК) демонстрирует лишь некоторые потенциальные достоинства этой концепции, а, именно, (А) упрощение технологии изготовления, неизмеримо более высокая точность характеристик фильтра в сравнении с ARC – реализацией и (В) возможность реализации «отрицательного резистора». Принцип переключаемых конденсаторов нашел применение не только в составе фильтров, но, даже в большей степени, – в цифроаналоговых и аналого-цифровых преобразователях и других субсистемах дискретно-аналоговой обработки сигнала, являющихся одними из главных субсистем любой цифровой системы связи. В связи с широчайшим использованием принципа ПК, существует необходимость обозначить достаточно «плавный» переход от классического преобразования Лапласа, как метода анализа схем непрерывного времени, к методу анализа аналоговых схем дискретного времени

Рассмотрим схему, дискретизирующую аналоговый сигнал, на рис.1.18.

Рис. 1.18. Схема дискретизации аналогового сигнала.

Ключ , замыкаясь в моменты времени Т, 2Т, 3Т, …, моментально заряжает конденсатордо мгновенного значения входного сигналав эти же моменты Т, 2Т, 3Т, … и через бесконечно короткое время размыкается. На конденсаторе запоминаются мгновенные значения входного сигнала. Эти значения сигнала держится в течение времени, и затем ключмгновенно разряжает конденсатор до нуля. На выходе дискретизатора находится буфер с коэффициентом усиления.

Дискретизированный эквивалент непрерывного входного сигнала изображен на рис. 1.19.

Определим ступенчатую функцию . Пустьприипри. Тогдаn – й отсчет функцииможно представить в виде:

(1.49)

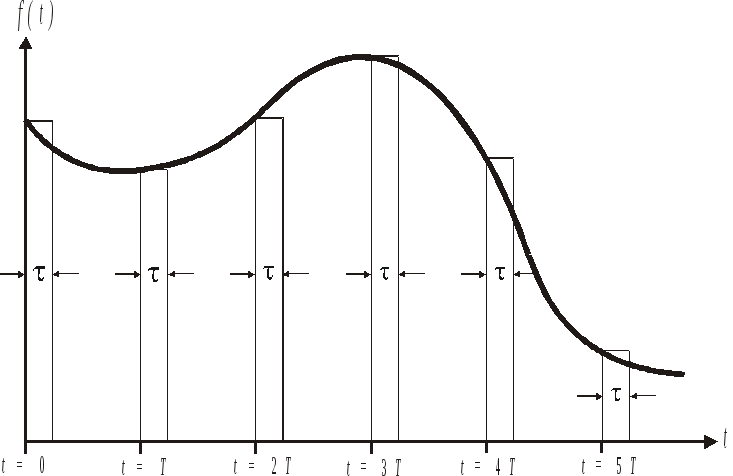
Рис. 1.19. Дискретизированный эквивалент непрерывного входного сигнала .

Определим ступенчатую функцию . Пустьприипри. Тогдаn – й отсчет функцииможно представить в виде:

(1.50)

Предполагая при, дискретизированный эквивалентэтой функции можно записать:

(1.51)

Произведем для дискретизированного сигнала преобразование Лапласа и найдем его изображение. Учитывая что, а также, получаем:

(1.52)

Пусть ширины импульсов, представляющих функцию, очень малы, тогда в (1.44) можно записать:

(1.53)

В выражении для положим, т.е. пусть не амплитуда, аплощадь каждого импульса функции равна, и выражение (1.50) запишется в виде:

(1.54)

где . Выражение (1.52) называется– преобразованием дискретных выборокфункции.

Из выражения (1.52) следует правило, чрезвычайно часто используемое в дискретных во времени системах, как цифровых, так и аналоговых: каждая выборка в z-области, задержанная на период сигнала дискретизации, отличается от не задержанной на множитель .

Поскольку z-преобразование является таким же интегральным преобразованием, как и преобразование Лапласа, все свойства -преобразования практически повторяют свойства преобразования Лапласа, но с учетом (1.46), т.е.. В настоящем пособииz-преобразование использовано для определения передаточных функций дискретных во времени ПК интеграторов, как без задержки (на рис. 1.12), так и с задержкой (на рис. 1.14).