1.2. Примеры расчета передаточных функций некоторых пассивных

линейных схем

В аналоговой схемотехнике рассматриваются схемы обработки сигнала. По умолчанию предполагается, что сигнал представляет собой переменное и непредсказуемое значение, либо тока, либо напряжения. Если бы его значение всегда можно было бы предсказать, этот сигнал потерял бы для нас интерес, и для его обнаружения и измерения не требуется создавать аналоговые схемы, чему посвящен настоящий курс.

Осциллограмма типового сигнала (например, человеческая речь) выглядит шумоподобной, т.е. ее значения, как превышающие некоторую постоянную составляющую (отсутствие сигнала), так и меньшие ее, являются равновероятными. По этой причине практически в любом аналоговом узле в качестве постоянной составляющей напряжения (напряжение на сигнальном проводе при отсутствии сигнала) принято напряжение, равноудаленное от потенциалов источника (источников) питания. В случае одного источника питания потенциал постоянной составляющей равен половине напряжения питания, т.е. . Ввиду особого его расположения и значения, этот потенциал называют потенциалом «аналоговой земли». В дальнейшем выражение «аналоговая земля», в том или ином падеже, будем использоватьбез кавычек.

1.2.1. Пассивный rc фильтр низких частот первого порядка

Проведем анализ этой простейшей частотозависимой линейной схемы, представленной на рис. 1.1. Эту схему называют интегрирующей RC цепочкой, что следует из уравнения Кирхгофа для оригинала схемы (во временнòй области):

, (1.5)

откуда после интегрирования (1.6)

Определим характеристики схемы в частотной области, пользуясь методом преобразования Лапласа.

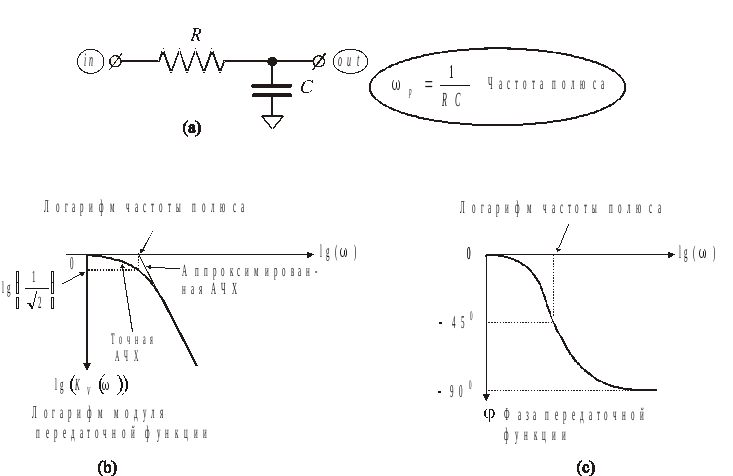
Рис. 1.1: (а) пассивный RC фильтр низких частот первого порядка: (b) зависимость коэффициента передачи от частоты; (с) зависимость сдвига фазы между входным и выходным сигналами от частоты.

Напомним известную из курса теоретической электротехники передаточную функцию пассивного RC фильтра в стационарном состоянии. Для ее получения используем законы Кирхгофа, справедливые как для оригиналов, так и для изображений токов:

Очевидно, что , т.е.(1.7)

Передаточная функция:

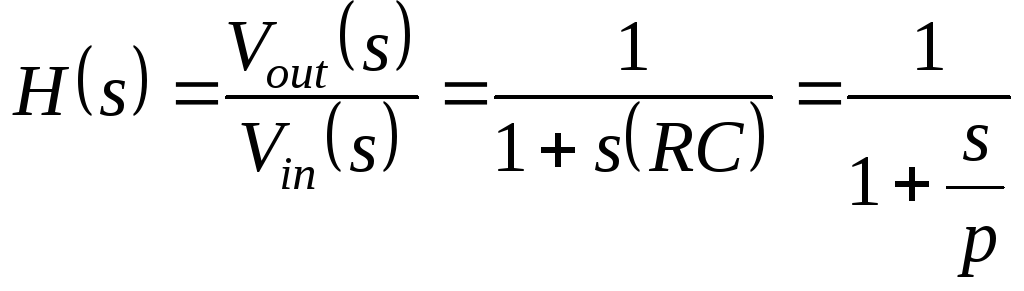(1.8)

Здесь – действительный полюс передаточной функции.

Для стационарного состояния , поэтому

(1.9)

Модуль комплексного выражения (1.7) определяет зависимость от частоты коэффициента передачинапряжения с входана выходрассматриваемого фильтра:

(1.10)

Сдвиг фазы между напряжениямииопределяется выражением:

(1.11)

На малых частотах, при которых круговая частота сигнала много меньше собственной круговой частоты полюса передаточной функции, т.е. , выражение длязначительно упрощается и аппроксимируется выражением:

(1.12)

На высоких частотах, при которых круговая частота сигнала много больше собственной круговой частоты полюса передаточной функции, т.е. , выражение длятакже упрощается, и соответствующая аппроксимация имеет вид:

(1.13)

Иллюстрации точных и аппроксимированных зависимостей от частоты коэффициента передачи и разности фазмежду входным и выходным сигналами представлены на рис. 1.1(b) и 1.1(с) соответственно.