1.2.2. Простейший пассивный rlc фильтр низких частот

На рис. 1.2 изображен известный RLC фильтр низких частот второго порядка.

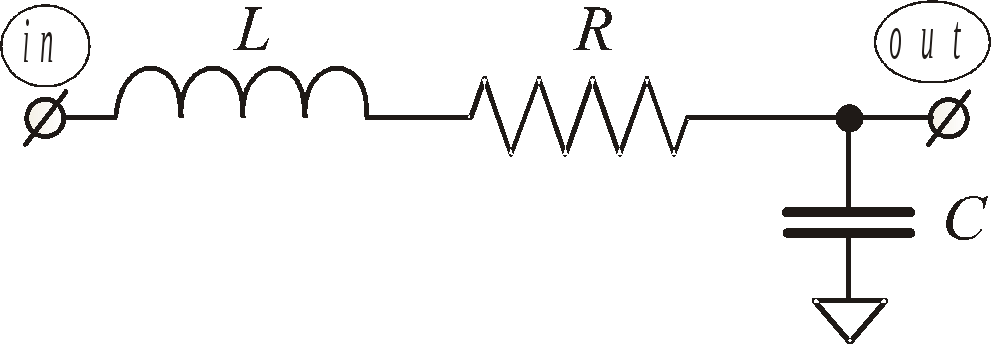
Рис. 1.2. Пассивный RLC

фильтр низких частот

второго порядка.

Поскольку пассивный RLC фильтр имеет 2 узла (узел ина рис. 1.2), то имеем 2 уравнения Кирхгофа:

(1.14а)

(1.14b)

Передаточная функция:

(1.15)

При резонансе на частоте имеемравным, откуда

(1.16а)

Одно из определений добротности использует соотношение, из которого можно получить 3 выражения для:

;;(1.16b)

С учетом (1.14а) и (1.14b) перепишем выражение (1.13) в каноническом виде:

(1.17)

1.3. Примеры расчета передаточных функций простейших активных

линейных схем аналоговой обработки сигналов

Операционный усилитель (ОУ) является ядром схем, выполняющих математические операции с аналоговыми сигналами. Приведем простые примеры использования ОУ в функциональных блоках, производящих математические операции с аналоговым сигналом, с целью получения с помощью уравнений Кирхгофа передаточных функций этих блоков. Из анализа передаточных функций будет с очевидностью ясна роль величины дифференциального коэффициента усиления ОУ.

В приведенных ниже примерах ОУ рассматривается как линейная субсистема со своей передаточной функцией . Как будет показано в главеII, модуль передаточной функции, являющийся коэффициентом усиления усилителя, уменьшается при увеличении частоты сигнала, однако в области частот, меньших частоты первого полюса (низкочастотный режим), модуль коэффициента усиления можно считать постоянным и равным максимальному значению, а разность фаз между входным и выходным сигналами можно считать равной нулю. При этом условии передаточная функциявырождается в единственное действительное число.

Итак, пусть используемые в примерах входной (и, соответственно, выходной) сигнал ОУ имеют низкие частоты, а также постоянные и конечные значения дифференциальных коэффициентов усиления, равные (так называемое «низкочастотное приближение»).

1.3.1. Неинвертирующий усилитель

На рис. 1.3 изображена функциональная схема неинвертирующего усилителя. При конечном значении низкочастотного коэффициента усиления ОУ и любом напряжениина выходе ОУ разностью потенциалов инвертирующего и неинвертирующего входов, строго говоря, НЕЛЬЗЯ пренебрегать.

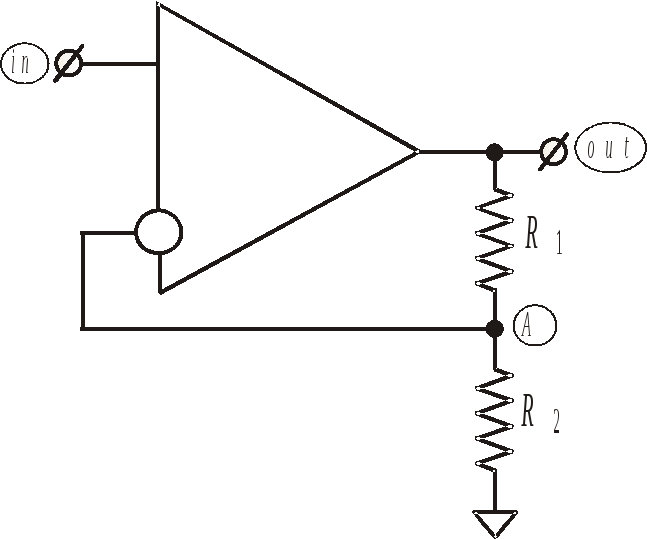
Рис. 1.3. Неинвертирующий

усилитель.

При этом условии имеем следующие два (по количеству узлов с изменяющимися и одновременно неизвестными потенциалами) линейных уравнений Кирхгофа для схемы на рис. 1.3 (потенциал неинвертирующего входа принимается равным аналоговому нулю, то есть половине напряжения питания):

(1.18а)

(1.18b)

Решая систему линейных уравнений (1.16), получаем:

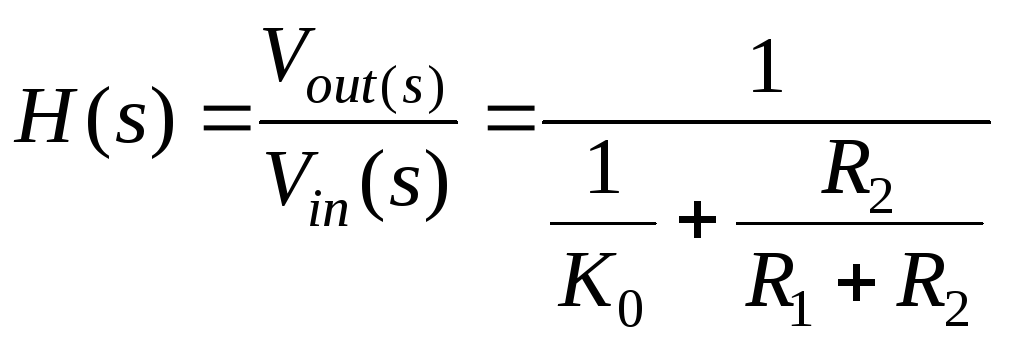(1.19а)

Если , то (1.19b)

Последнее выражение является хорошо известным из большинства учебников по аналоговой схемотехнике.