1.5.5. Неинвертирующий пк интегратор с задержкой

На рис. 1.14 представлена схема неинвертирующего интегратора с задержкой на базе инвертирующего ПК с задержкой. Рассматриваемый интегратор является неинвертирующим, поскольку состоит из инвертирующего ПК, подключенному к инвертирующему же входу операционного усилителя (ОУ).

Согласно (1.42), в момент времени из правой обкладки конденсаторачерез ключSw2 в узел А инвертирующего входа ОУ вносится заряд, равный . Если , то привнесенный в узел А заряд изменяет потенциал узла в отрицательную сторону и, соответственно, потенциал выходного узлаизменяется в положительную сторону. При этом в правую обкладку инвертирующего конденсаторавносится положительный заряд, и такой же положительный заряд «выталкивается» из левой обкладки в узел А, компенсируя находящийся там отрицательный заряд, «вытолкнутый» из левой обкладки.

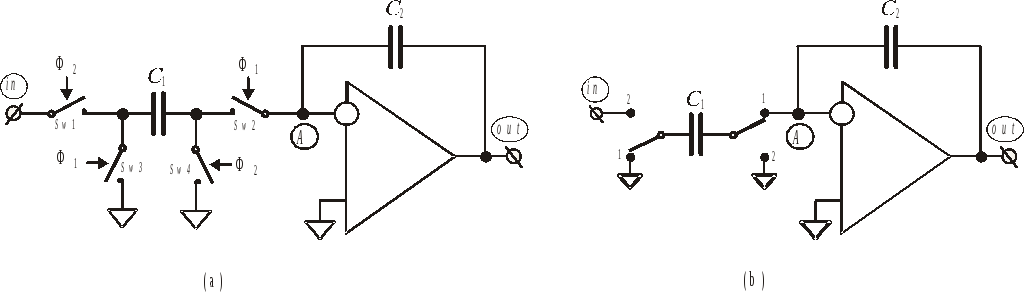
Рис. 1.14. Неинвертирующий ПК интегратор с задержкой:

(а) с подробным изображением ключей; (b) с условными перекидными

ключами

При идеальных ключах и ОУ процессы компенсации и установления соответствующего потенциала на выходе интегратора происходят мгновенно, т.е. уже непосредственно в момент времени выходной потенциал заканчивает изменяться на величину, достаточную для компенсации зарядов в узле А. В реальности процесс компенсации проходит за промежуток времени, равный половине периода, отдо, пока узел А ещеотрицателен относительно неинвертирующего входа ОУ. При положительном изменении выходного потенциала и сравнивании потенциалов обоих входов ОУ (при отсутствии смещения нуля в идеальном ОУ), величина положительного заряда величины

, (1.45)

«вытолкнутого» из левой обкладки конденсатора , сравнивается с величиной отрицательного заряда, «вытолкнутого» из правой обкладкии равного

(1.46)

Таким образом, для изменения напряжения на выходе ПК интегратора с задержкой можно записать:

(1.47а)

Поскольку в промежуток времени от доключSw2 разомкнут и левая обкладка конденсатора является плавающей, то заряд конденсаторавеличины сохраняется до момента . По этой причине промежуток времени отдоназывается временемхранения, и выражение (1.47а) можно дополнить:

(1.47b)

1.6. Реализация биквада на базе переключаемых конденсаторах

прямой заменой резисторов на переключаемые конденсаторы

Предположим, что резисторы имитируются переключаемым конденсатором (ПК) с частотой переключения , много большей наивысшей частотысигнала на входе фильтра. В этом случае номиналрезистора вARC реализации (в первом приближении) заменяется на эффективное сопротивление, определяемое выражением

, (1.48)

где номинал соответствующего переключаемого конденсатора определяется из этого же выражения (1.38). Одной из трудностей классическойARC реализации биквада является необходимость наличия в составе биквада отрицательного резистора. При использовании ОУ с недифференциальными выходами требуется введение в состав биквада дополнительного активного инвертора сигнала (пример активного инвертора – инвертирующий усилитель на рисунке 1.4 с одинаковыми резисторами и). Красивым решением является использование полностью дифференциальных операционных усилителей (см. рис. 1.9), и, хотя такое решение удваивает количество пассивных компонентов, оно применяется практически везде, где нужны фильтры на базе ПК, по причине радикального снижения чувствительности к помехам и увеличения быстродействия.

При проектировании биквада на базе переключаемых конденсаторов с ОУ, имеюших недифференциальные выходы, применение инверторов сигналя принципиально НЕ является необходимым, поскольку существует инвертор заряда, описанный выше как инвертирующий переключаемый конденсатор. Схема биквада на базе ОУ с недифференциальным выходом после прямой замены резисторов на ПК (включая неинвертирующие ПК и один инвертирующий), приведена на рис. 1.14.

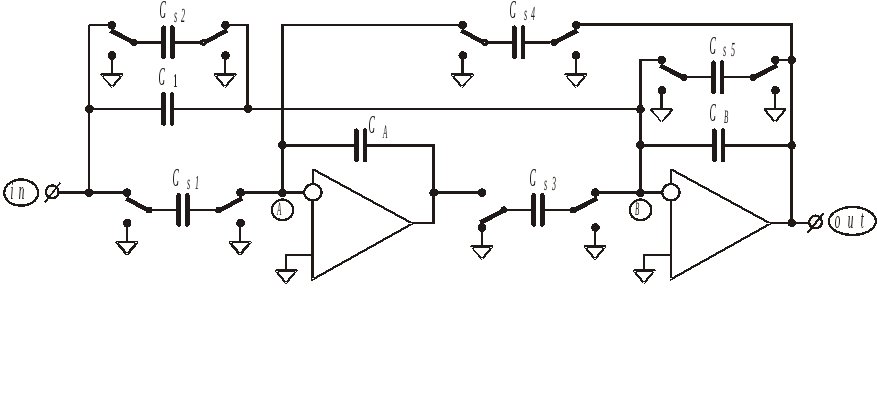
Рис. 1.15. Реализация биквада при прямой замене резисторов на ПК.

Отметим, что у некоторых переключаемых конденсаторов, например, C_S1 и С_S2, левые обкладки имеют одинаковый потенциал в любом из положений ключей, что позволяет объединить эти обкладки и подключать к соответствующим узлам с помощью единственного ключа. Одинаковый потенциал имеют также правая обкладка C_S1 и левая обкладка C_S4, правые обкладки C_S2 и C_S3 и левая обкладка C_S5, правые обкладки C_S4 и C_S5. Благодаря этому обстоятельству, схему можно упростить (оптимизировать). Оптимизированный вариант биквада на базе ПК представлен на рис. 1.15.

Рис. 1.16. Оптимизированная реализация биквада на рис. 1.15 на базе ОУ с одним выходом после объединения узлов с одинаковыми потенциалами.

Оптимизированная реализация полностью дифференциального ПК биквада представлена на рис. 1.17.

Рис. 1.17. Оптимизированная реализация полностью дифференциального ПК биквада