
- •1. Введение в анализ и синтез базовых узлов линейной обработки
- •1.1. Преобразование Лапласа как метод анализа линейных схем
- •1.2. Примеры расчета передаточных функций некоторых пассивных
- •1.2.1. Пассивный rc фильтр низких частот первого порядка
- •1.2.2. Простейший пассивный rlc фильтр низких частот
- •1.3. Примеры расчета передаточных функций простейших активных
- •1.3.1. Неинвертирующий усилитель
- •1.3.2. Инвертирующий усилитель
- •1.3.3. Активный инвертирующий интегратор
- •1.4. Введение в реализацию arc биквада
- •1.4.1. Принцип масштабирования пассивных элементов в arc фильтрах
- •1.5. Введение в концепцию переключаемых конденсаторов
- •1.5.1. Неинвертирующий переключаемый конденсатор с задержкой,
- •1.5.2. Неинвертирующий переключаемый конденсатор без задержки,
- •1.5.3. Инвертирующий пк интегратор без задержки, не чувствительный
- •1.5.4. Инвертирующий переключаемый конденсатор с задержкой,
- •1.5.5. Неинвертирующий пк интегратор с задержкой
- •1.6. Реализация биквада на базе переключаемых конденсаторах
- •1.7. Дискретизация аналогового сигнала. Идеальные выборки
- •1.7.1. Передаточная функция пк интегратора без задержки
- •1.7.2. Передаточная функция пк интегратора с задержкой
- •Модели элементов интегральных схем
- •3. Базовые элементы кмдп операционных усилителей
- •3.1. Простейший усилитель напряжения с общим истоком
- •3.1.1. Простейший усилительный каскад с общим истоком и активной
- •3.1.2. Малосигнальные характеристики простейшего кмдп усилителя
- •3.1.3. Частота единичного усиления простейшего усилителя
- •3.1.4. Соотношение малосигнальных параметров простейшего
- •3.1.5. Простейший усилитель в режиме большого сигнала
- •3.1.6. Расчет выходного сопротивления
- •3.1.7. Элементарный анализ величины входной емкости. Емкость Миллера
- •3.1.8. Пример топологии простейшего усилителя
- •3.2. Выходное сопротивление и коэффициент передачи каскада с диодом в нагрузке
- •3.3. Токовое зеркало
- •3.3.1. Формирование режимных потенциалов в простейшем усилителе с общим истоком
- •3.4. Истоковый повторитель
- •3.4.1. Выходное сопротивление и входная емкость истокового
- •3.5. Метод увеличения выходного сопротивления усилителя
- •3.6. Каскодный усилитель
- •3.6.1. Передаточная функция простейшего каскодного усилителя с идеальной токовой нагрузкой
- •3.6.2. Роль емкости в выходном узле каскодного усилителя.
- •3.6.3. Диапазон изменения выходного напряжения
- •3.6.4. Схемы формирования постоянного смещения на затворе каскодного транзистора.
- •3.6.5. Каскодное токовое зеркало
- •3.6.6. Самосмещаемое каскодное токовое зеркало
- •3.7. Концепция активного каскодного транзистора (материал для дополнительного изучения подготовленными студентами с использованием периодической литературы)
- •3.8. Дифференциальный каскад
- •3.8.1. Допустимый диапазон входного синфазного напряжения
- •3.8.2. Дифференциальный каскад как источник тока, управляемый входным напряжением. Несимметричный и симметричный входные сигналы
- •4. Архитектуры кмдп операционных усилителей
- •4.1. Методика оценки малосигнальных характеристик операционного усилителя
- •4.1.1. Методика замены нескольких действительных неосновных полюсов в передаточной функции операционного усилителя одним «эффективным» неосновным полюсом
- •4.1.2. Расчет запаса фазы операционного усилителя с действительными
- •4.2. Однокаскадные операционные усилители как операционные
- •4.2.1. «Телескопический» оитун
- •4.2.1.1. Базовые характеристики «телескопического» оитун
- •4.2.1.2. Упрощенная методика расчета фазы в «телескопическом» усилителе
- •4.2.1.3. Оценка частот неосновных полюсов «телескопического» оитун
- •4.2.1.4. Анализ переходных процессов
- •4.2.2. «Согнутый» каскодный оитун с р-канальным входом
- •4.2.2.1. Диапазоны входного синфазного и выходного напряжений
- •4.2.2.2. Режим малого сигнала
- •4.2.2.3. Переходной процесс в режиме большого сигнала
- •4.2.3. «Согнутый» каскодный оитун с n-канальным входом
- •4.3. Двухкаскадный операционный усилитель (оитун)
- •4.3.1. Базовая схема двухкаскадного оитун
- •4.3.2. Эквивалентная малосигнальная схема двухкаскадного усилителя
- •4.3.3. Передаточная функция двухкаскадного усилителя
- •4.3.4. Соотношение частот неосновного полюса, нуля и частоты единичного усиления
- •4.3.5. Частота единичного усиления двухкаскадного оитун
- •4.3.7. Реакция двухкаскадного оитун на большой входной сигнал.
- •4.3.8. Реакция двухкаскадного оитун на большой синусоидальный
- •4.3.9. Распространенная архитектура двухкаскадного оитун
- •5. Шум и его анализ в кмдп аналоговых имс
- •5.1. Основные определения
- •5.1.1. Cуммирование шумов
- •5.1.2. Анализ шума в частотной области
- •5.2. Пример расчета шума arc фильтра первого порядка
- •5.2.1. Реакция на шумовой источник тока
- •5.2.2. Реакция на шумовой источник тока
- •5.2.3. Реакция на шумовой источник напряжения
- •5.4. Приведенный ко входу собственный «белый» шум повторителя
- •5.5. Собственный шум многокаскадного усилителя
- •5.6. Шум каскодного усилителя
- •6. Полностью дифференциальные оитун
- •6.1. Базовая архитектура полностью дифференциальных схем
- •6.2. Принципиальные преимущества полностью дифференциальных схем
- •6.2.1. Зависимость потенциала общего истока дифкаскада от сигнала
- •6.3. Принципиальные недостатки полностью дифференциальных схем
- •6.4. Варианты непрерывных во времени схем синфазной обратной связи (сос).
- •6.4.1. Схема с ограниченным диапазоном входных сигналов.
- •6.4.2. Непрерывная во времени cхема сос с максимальным диапазоном
- •6.4.3. Варианты схем синфазной обратной связи на базе переключаемых конденсаторов
5.1. Основные определения
Несмотря на равенство нулю средней величины шума, физически он существует, и квадрат величины шума не равен нулю. Определяют среднеквадратичную величину (Mean Root Square) шума (Noise):
 - для шумового
напряжения (5.1)
- для шумового
напряжения (5.1)
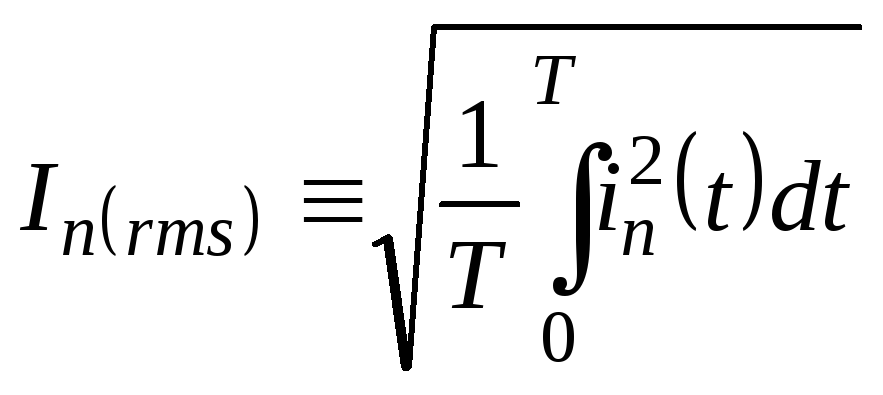 - для шумового
тока (5.2)
- для шумового
тока (5.2)
здесь
![]() – интервал времени усреднения. Чем
больше интервал времени
– интервал времени усреднения. Чем
больше интервал времени![]() ,
тем точнее величины
,
тем точнее величины![]() и
и![]() .
Очевидно, что квадраты величин в (5.1) и
(5.2) естьмощность,
рассеиваемая
в резисторе 1 Ом, если к нему приложены
среднеквадратичное напряжение
.
Очевидно, что квадраты величин в (5.1) и
(5.2) естьмощность,
рассеиваемая
в резисторе 1 Ом, если к нему приложены
среднеквадратичное напряжение
![]() или постоянное, численно равное ему, а
также если через резистор 1 Ом течет
среднеквадратичный ток
или постоянное, численно равное ему, а
также если через резистор 1 Ом течет
среднеквадратичный ток![]() или постоянный, численно равный ему.
или постоянный, численно равный ему.
Отношение сигнала
к шуму
![]() (Signal
to
Noise
Ratio)
определяется
так:
(Signal
to
Noise
Ratio)
определяется
так:
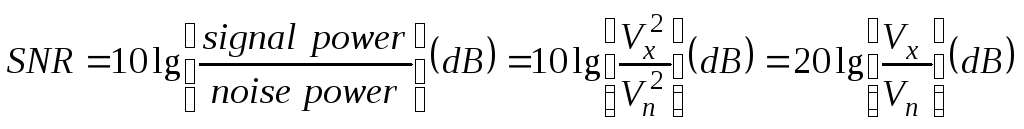 (5.3)
(5.3)
Здесь
![]() – мощность сигнала,
– мощность сигнала,![]() – мощность шума.
– мощность шума.
Хотя децибелы (дБ) по определению относятся к отношению двух величин, оказалось полезным введение определение величины мощности в дБ для абсолютных значений сигнала. Условно принято, что мощность, равная 1 мВт называется 1дБм (1dBm). Например, мощность в 1 мкВт обозначается как –30 (дВм). В случае обозначения в (дВм) напряжений, определяют 1 дБм (dBm) как напряжения (среднеквадратичные или постоянные) на ряде резисторов (600 Ом, 75 Ом и 50 Ом), при которых рассеиваются одинаковые мощности в 1 мВт.
5.1.1. Cуммирование шумов
Рассмотрим случай соединенных последовательно источников шумового напряжения и соединенных параллельно источников шумового тока (рис. 5.1).
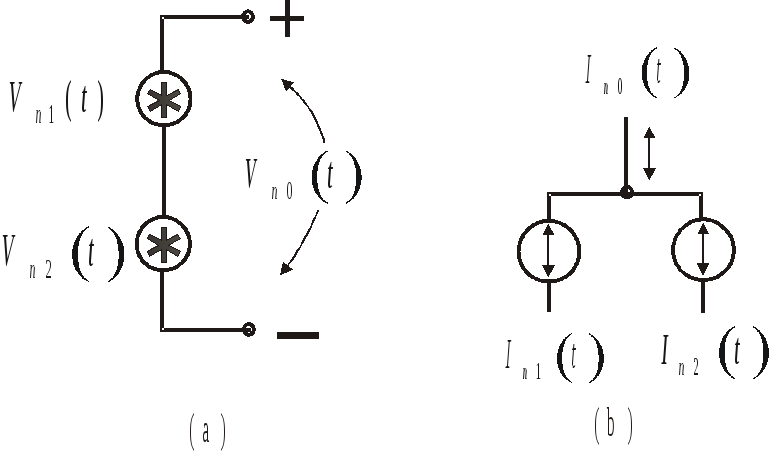
Рис.5.1. Суммирование двух
шумовых источников:
(а) напряжения и (b) тока.
Определим
![]() как
как![]() (5.4)
(5.4)
Тогда
![]() (5.5)
(5.5)
Первые два члена в правой части (5.5) – мощности шумов обоих источников. Последний член выражает корреляцию между источниками шума. Принято определять корреляцию С следующим образом:
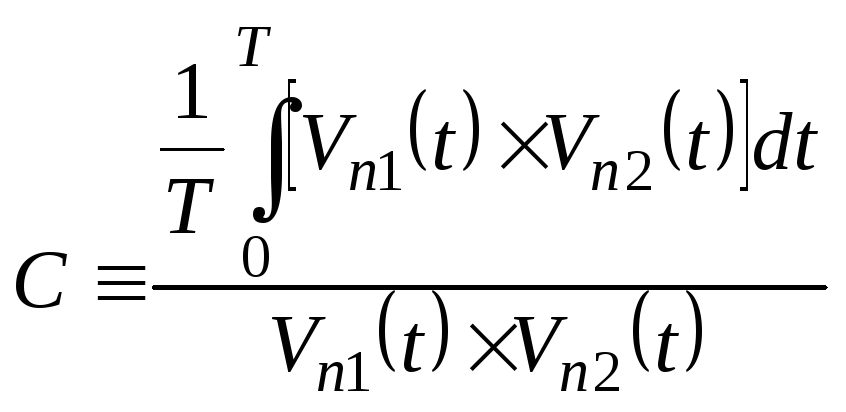 (5.6)
(5.6)
С учетом этого определения (5.5) можно записать:
![]() (5.7)
(5.7)
Коэффициент
корреляции С
удовлетворяет неравенству
![]() .
Если
.
Если![]() ,
то два сигналаполностью
коррелированы,
если же
,
то два сигналаполностью
коррелированы,
если же
![]() ,
то сигналынекоррелированы.
Промежуточные значения С
означают частичную корреляцию.
,
то сигналынекоррелированы.
Промежуточные значения С
означают частичную корреляцию.
В случае двух некоррелированных сигналов
![]() (5.8)
(5.8)
В случае же полностью коррелированных сигналов (например, двух синусоидальных сигналов с одинаковыми частотами и с фазами 0 или 180 градусов)
![]() (5.9)
(5.9)
В усилительных электронных схемах конкретная величина шума в большинстве случаев много меньше установленных или ожидаемых величин тока или напряжения, поэтому можно считать, что шумовые напряжения и токи не влияют на характеристики компонентов, зависящие от тока и/или напряжения (например, крутизна транзистора), и шумовые напряжения двух последовательно включенных приборов (или шумовые токи двух параллельно включенных приборов) взаимно не коррелируют.
5.1.2. Анализ шума в частотной области
Ввиду случайности
и непредсказуемости значений шумового
сигнала, его мощность
![]() (или
(или![]() )
непрерывно распределена в частотной
области. Ввидунепрерывного
распределения,
в бесконечно
малой полосе частот
мощность шума равна нулю!
Когда говорят о конкретной спектральной
плотности шума на какой-то частоте, то
по умолчанию имеют в виду мощность шума
в частотной полосе 1 Гц, и упомянутая
частота находится в середине этой
полосы. Полная мощность шума получается
интегрированием плотности шума по всему
спектру частот:
)
непрерывно распределена в частотной
области. Ввидунепрерывного
распределения,
в бесконечно
малой полосе частот
мощность шума равна нулю!
Когда говорят о конкретной спектральной
плотности шума на какой-то частоте, то
по умолчанию имеют в виду мощность шума
в частотной полосе 1 Гц, и упомянутая
частота находится в середине этой
полосы. Полная мощность шума получается
интегрированием плотности шума по всему
спектру частот:
![]() (5.10)
(5.10)
Рассмотрим
прохождение шумового сигнала
![]() через фильтр с передаточной функцией
через фильтр с передаточной функцией![]() .
Спектральная плотность
.
Спектральная плотность![]() мощности шума на выходе фильтра равна:
мощности шума на выходе фильтра равна:
![]() (5.11)
(5.11)
Полная мощность
шума
![]() равна
равна
![]() (5.12)
(5.12)
Среднеквадратичное
значение плотности шума
![]() равно
равно
![]() (5.13)
(5.13)
Поскольку среднеквадратичное значение шума определяется обычным для линейного фильтра образом, посредством модуля передаточной функции, а не через ее квадрат, удобно пользоваться среднеквадратичным значением, а не мощностью шума.
Предположим теперь,
что шум на выходе системы
![]() является суммой
является суммой![]() входных шумовых сигналов
входных шумовых сигналов![]() ,
и каждый входной шумовой сигнал
,
и каждый входной шумовой сигнал![]() проходит через фильтр
проходит через фильтр![]() .
Тогда спектральная плотность
.
Тогда спектральная плотность![]() шума на выходе:
шума на выходе:
![]() (5.14)
(5.14)
Если шумовые сигналы взаимно не коррелированы, то на выходе фильтров они также не коррелированы.
5.1.3. Белый шум
«Белый шум»
определяется
как шум с постоянной и не зависящей от
частоты спектральной плотностью шума.
Наиболее известный источник белого
шума – резистор. Шум резистора моделируется
как включенный последовательно с
резистором источник напряжения со
спектральной плотностью
![]() :
:
![]() (5.15а)
(5.15а)
Здесь
![]()
![]() .
.
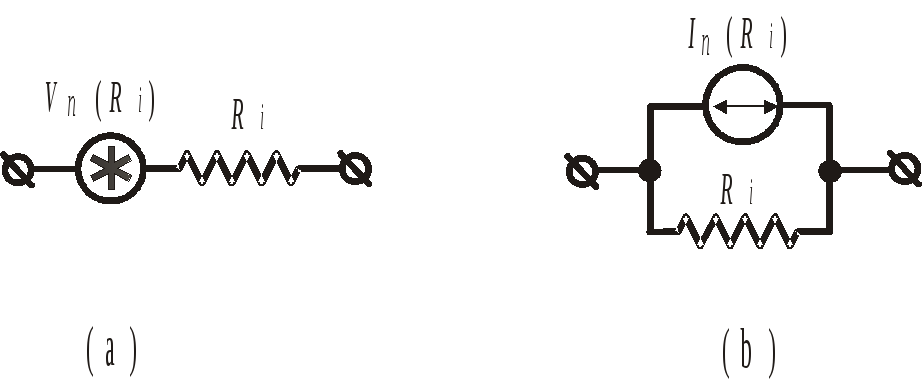
Рис. 5.2. Эквивалентная схема шумящего резистора:
(a) – присоединенный последовательно источник шумового напряжения;
(b) – присоединенный параллельно источник шумового тока.
Следует отметить,
что на общепринятом изображении шумящего
резистора Ri
с присоединенным последовательно
источником шумового напряжения
![]() символ самого источника шума ни в коей
мере нельзя рассматривать как
самостоятельный источник напряжения.
В этой связи, например, на Рис. 5.2.аотсутствует
узел между символами источника напряжения
и резистора,
поскольку
их необходимо рассматривать как одно
целое. Это необходимо учитывать при
анализе и составлении уравнений Кирхгофа.
символ самого источника шума ни в коей
мере нельзя рассматривать как
самостоятельный источник напряжения.
В этой связи, например, на Рис. 5.2.аотсутствует
узел между символами источника напряжения
и резистора,
поскольку
их необходимо рассматривать как одно
целое. Это необходимо учитывать при
анализе и составлении уравнений Кирхгофа.
Наряду с моделью
(5.15) в равной степени используется модель
шума резистора как включенный параллельно
с резистором источник тока со спектральной
плотностью
![]() :
:
![]() .
(5.15b)
.
(5.15b)
5.1.4. Полоса шума
Как известно, идеальным фильтром является фильтр с прямоугольной АЧХ, в пределах которой модуль коэффициента передачи (усиление) равен единице, а в полосе задерживания равен нулю. Реальные фильтры имеют неравномерность АЧХ в полосе пропускания, конечный наклон в переходной полосе и отличное от нуля пропускание в полосе задерживания.
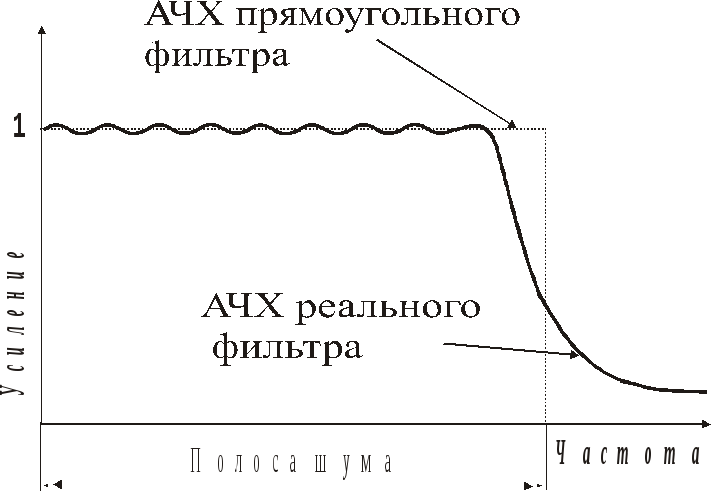
Рис.5.3. Реальный и идеальный
фильтры с идентичными
мощностями выходного шума
при одинаковых спектральных
плотностях белого шума
на входах.
Под полосой шума понимают полосу пропускания идеального прямоугольного фильтра низкой частоты, шум на выходе которого такой же, как на выходе рассматриваемого реального фильтра, при условии подключения на входы обоих фильтров одинаковых источников белого шума.
Представительным примером фильтра является пассивный RC фильтр первого порядка. Модулем его передаточной функции (зависимость коэффициента передачи от частоты) является выражение
![]() (5.16)
(5.16)
где
![]() – частота действительного полюса
пассивногоRС
фильтра.
– частота действительного полюса
пассивногоRС
фильтра.
Подсоединим ко входу фильтра источник белого шума с независящей от частоты спектральной плотностью:
![]() (5.17)
(5.17)
Полная мощность
![]() шума, прошедшего через фильтр, равна:
шума, прошедшего через фильтр, равна:
 (5.18)
(5.18)
Такой же по величине,
но прошедший через идеальный прямоугольный
фильтр низкой частоты с полосой
![]() ,
шум равен:
,
шум равен:
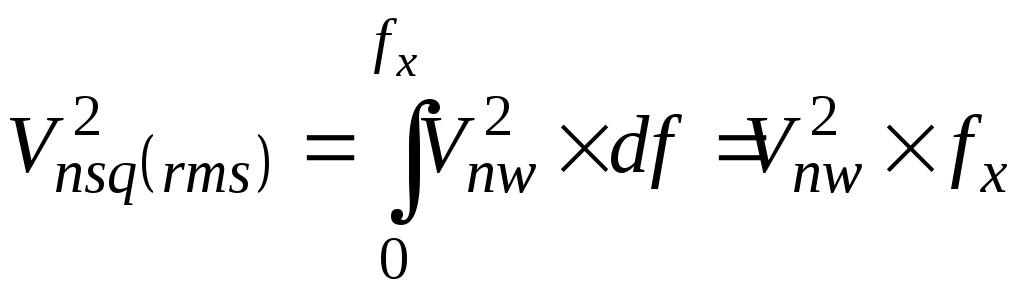 (5.19)
(5.19)
Из сравнения (5.18) и (5.19) получаем:
![]() (5.20)
(5.20)
Рассчитаем выражение для полной мощности шума напряжения на конденсаторе пассивного RC фильтра с шумящим резистором:
![]() (5.21)
(5.21)
Назначение приведенных выше выкладок – в том числе для получения фундаментального выражения (5.21), используемого при анализе аналоговых схем на переключаемых конденсаторах.
