5.2.3. Реакция на шумовой источник напряжения

Базовая реакция сводится к тому, что все шумовое напряжение приложено к неинвертирующему входу ОУ. Поскольку, как условлено выше, ОУ является идеальным и имеет бесконечное усиление, потенциал на инвертирующем входе полностью повторяет потенциал неинвертирующего входа.

Спектральная плотность шума на выходе от шумового источника :

(5.28)

5.2.4. Реакция на приведенный ко входу источник напряжения

эквивалентного шума Операционного Усилителя

Удобнее всего такой источник напряжения разместить на неинвертирующем входе. Анализ аналогичен анализу реакции от резистора R2, поэтому и результат также аналогичен:

(5.29)

Полная мощность шума на выходе фильтра равна интегралу по частоте суммы спектральных плотностей шума от всех источников шума:

(5.30)

5.3. Пример расчета приведенного ко входу шума КМДП дифференциального

каскада с активной нагрузкой

На рис. 5.6 изображен КМДП дифференциальный каскад с активной нагрузкой. В цепь затвора каждого транзистора включен воображаемый эквивалентный источник приведенного к затвору шумового напряжения.

Пусть источник режимного тока на М0 по умолчанию имеет большое выходное сопротивление. Это дает возможность считать, что, например, увеличение шумового тока в М1 на какую-либо величину, влечет уменьшение тока в М2 на такую же величину. Пусть упомянутое увеличение тока в М1 обязано собственному шуму М1. Таким образом, полный шумовой ток транзистора М1 поделен пополам между М1 и М2. Аналогично происходит и с шумовым током М2, т.е половина его течет в М2 и половина – в М1.

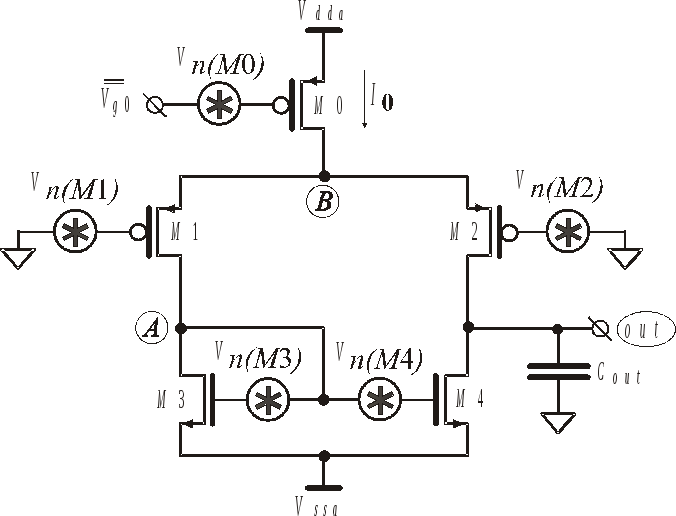
Рис.5.6. КМДП

дифференциальный

каскад с активной

нагрузкой и с

приведенными

ко входам источниками

шума.

Рассмотрим транзисторы М3 и M4. Как для М3, так и для М4, потенциалы истоков неизменны, поэтому собственные шумовые токи в них текут полностью. Однако, отметим, что M3 включен как диод, поэтому изменение тока в M3, обязанное шуму, влечет изменение превышения над порогом и, следовательно, потенциала узлаА. Дополнительно в транзисторе M3 протекает ток, в том числе и шумовой, транзистора M1 и, следовательно, половин шумовых токов транзисторов M1 и M2. Все перечисленные выше шумовые токи (шумовой ток M3 и половинки шумовых токов M1 и M2) модулируют потенциал узла А. Но с узлом А соединен затвор транзистора M4, и этот транзистор становится источником перечисленных выше в скобках токов, но – противоположного знака. Однако, из последнего следует, что «отраженные» в M4 половинки шумовых токов M1 и M2, протекающие в M3, находятся в фазе с теми половинками шумовых токов M1 и M2, которые протекали в M2. Шумовой ток M3 полностью «отражается» в M4, а «собственный» для M4 шумовой ток в нем протекает всегда.

Итак, в M4, а, следовательно, и в M2, и в выходной цепи дифкаскада, протекают полные шумовые токи четырех транзисторов: M1 – M4, и их квадраты арифметически складываются. Разумеется, совпадение фаз «первоначально» находившихся в M2 половинок шумовых токов M1 и M2 и «отраженных» половинок этих же токов возможно только в области относительно низких частот, когда можно пренебречь задержкой фазы из-за паразитных емкостей в узлах А и В.

Рассмотрим теперь шум, вызываемый в выходной цепи транзистором M0.

В идеальном дифкаскаде (сейчас рассматривается именно этот случай) в обоих его симметричных ветвях текут половинки синфазного шумового тока транзистора M0 и вызывают изменения потенциалов в узлах А и out. Одинаковые токи в ветвях вызывают одинаковые же потенциалы в этих узлах. Несмотря на высокое выходное сопротивление в узле out, при идентичности синфазных токов, протекающих через узлы А и out, тем не менее, изменение потенциала затвора транзистора M4 определяется именно потенциалом узла А, т.е. изменение потенциала в узле А задает потенциал на выходе дифкаскада.

Итак, синфазный ток (в рассматриваемом случае являющийся шумовым током транзистора-генератора режимного тока) вызывает именно такое изменение выходного потенциала,какое определяется низким выходным сопротивлением диода на транзисторе M3. Такую ситуацию также можно объяснить полной корреляцией токов через узлы А и out. Дифференциальный же ток от любого из четырех транзисторов M1 – M4, а также от суммы всех токов, вызывает изменение потенциала узлаout, определяемое высоким выходным сопротивлением этого узла. Отношение дифференциального шумового напряжения к синфазномуравно отношению выходных сопротивлений в узлахА и out:

(5.31)

Поскольку же в выходной цепи складываются квадраты шумовых токов и напряжений, то 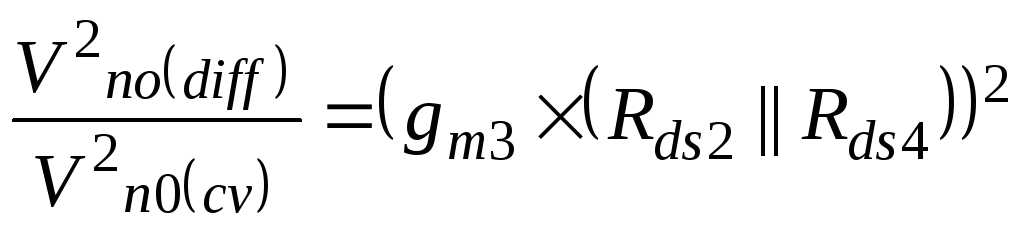(5.32)

Очевидно, что шумом транзистора М0, как синфазным, с полным правом можно пренебречь.

Итак, будем считать, что квадрат спектральной плотности шумового тока в выходной цепи дифкаскада на рис. 5.6 равен арифметической сумме спектральных плотностей шумовых токов четырех транзисторов (то же самое – и для квадрата полного шумового тока):

(5.33)

Используем известное соотношение для квадрата спектральной плотности шумового токатранзистора, где– квадрат крутизны этого транзистора, а– квадрат спектральной плотности приведенного ко входу шумового напряжения этого транзистора. Последнее является суммой квадратов приведенных ко входу транзистора спектральных плотностейдвух шумовых напряжений: во – первых, «белого» (независящая от частоты спектральная плотность) шума резистивного канала (5.34)

и, во – вторых, шума(5.35)

Здесь и– эффективные ширина и длина канала транзистора;– удельная емкость подзатворного диэлектрика;- частота, а– константа, зависящая от типа транзистора и, особенно, от технологического процесса.

Квадрат напряжения полного шума в диапазоне частот равен интегралу суммы спектральных плотностей (5.33) и (5.34) в этом диапазоне.

Квадрат полной спектральной плотности шумового тока каналов транзисторов равен, ввиду симметричности дифкаскада:

(5.36)

Пусть М1 является входным транзистором дифкаскада. Тогда квадрат спектральной плотности шумового напряжения , приведенный к затворуМ1 равен

(5.37)

Полная мощность шума на выходе дифкаскада равна интегралу по частоте суммы спектральных плотностей шума от транзисторов M1 – M4:

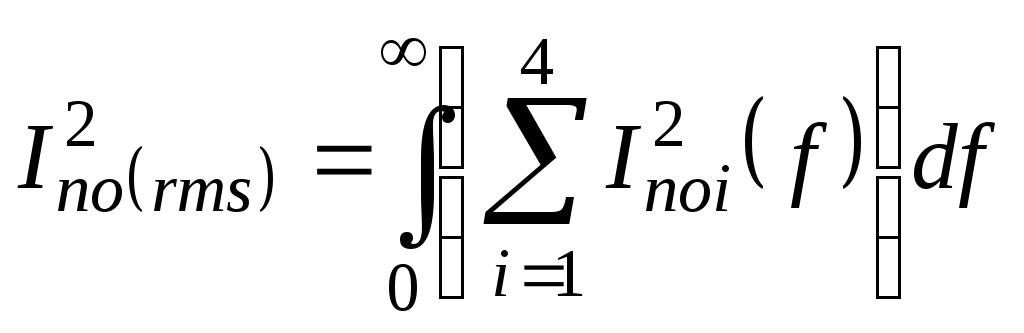(5.38)