3.1.3. Частота единичного усиления простейшего усилителя

Согласно (3.14), при частоте полюса коэффициент усиления усилителя. Если же принять во внимание упрощенные выражения (3.15) – (3.16) для модуля АЧХ, то, однако в любом случае коэффициент усилениядля типовых значенийзначителен, и для простейшего усилителя с длинами затвораот 0,25 мкм до 1,0 мкм обычно составляет от 10 до 100. В такой же мере (от 10 до 100 раз) частота единичного усилениябольше частоты полюса, поэтому на частотах, близких к, выражение (3.16) для коэффициента усиления справедливо с очень большой точностью. Используя (3.16), определим выражение для.

Поскольку , то можно написать:, откуда получаем:

(3.23)

3.1.4. Соотношение малосигнальных параметров простейшего

усилителя

Определим взаимное соотношение параметров и, а также покажем, чтообратно пропорционально .

В главе II показано, что (3.24)

Здесь – коэффициент пропорциональности.

Подставляем (3.18б) в (3.23) и выражаем следующим образом:

(3.25)

Подставляем (3.24) и (3.25) в (3.21) и получаем:

(3.26)

В практических разработках в большинстве случаев требуются усилители одновременно и с большим коэффициентом усиления, и с большой частотной полосой усиления, т.е. можно предложить «параметр качества» усилителя, равный произведению и:

(3.27)

Как видно из (3.27), находясь в рамках фиксированной электрической схемы усилителя (простейший усилитель с заданной емкостью нагрузки ) и фиксированной технологии (неизменные,и), соотношение (3.27) является фундаментальным, и увеличить параметр качества можно только увеличением ширины, сопровождаемым, однако, нежелательным пропорциональным увеличением потребляемого режимного тока. Очевидно, что увеличениеи, как совместное, так и по отдельности, является нетривиальной задачей и требует, как минимум, усложнения (часто весьма значительного) электрической схемы усилителя.

3.1.5. Простейший усилитель в режиме большого сигнала

Условие малого входного и/или выходного сигналов в i-узле определяется, как известно, соотношением . Условиембольшого сигнала является

. (3.28)

Режим большого сигнала означает, что, при подаче на вход усилителя (рис. 3.3) отрицательного скачка потенциала величиной , удовлетворяющего условию, входной транзисторзакроется, т.е. прекратит отводить часть тока нагрузочного транзистора из выходного узла в отрицательный источник напряжения. В результате весь ток нагрузочного транзистора течет в нагрузочную емкость, и потенциалвыходного узла увеличивается.

Входной транзистор, а также емкости P-N переходов стоков обоих транзисторов являются нелинейными элементами. Строго говоря, дифференциальная выходная проводимость нагрузочного транзистора в пологой области также является нелинейной, хотя в рамках упрощенной модели Level1 выходная проводимость принимается линейной. После отсечки входного транзистора нелинейная ВАХ входного транзистора перестает играть роль в начавшемся переходном процессе. Что касается нелинейных элементов, то, в подавляющем большинстве случаев:

– суммарная паразитная емкость нелинейных емкостей P-N переходов стоков обоих транзисторов много меньше емкости линейного конденсатора нагрузки , поэтому емкостьс большой точностью можно считать линейной;

– нелинейный характер заключается вотличии реальной ВАХ транзистора в пологой области от линейной. Экспериментальные ВАХ показывают, что их отличие от линейной аппроксимации, принятой в модели Level1 относительно незначительно.

Эквивалентная схема этой системы для сигнала на выходе усилителя в случае отсечки входного транзистора изображена на рис. 3.9. Поскольку приведенные выше доводы позволяют с достаточно большой точностью считать оставшуюся систему линейной, то уравнение Кирхгофа описывается линейным дифференциальным уравнением (полагаем):

(3.29)

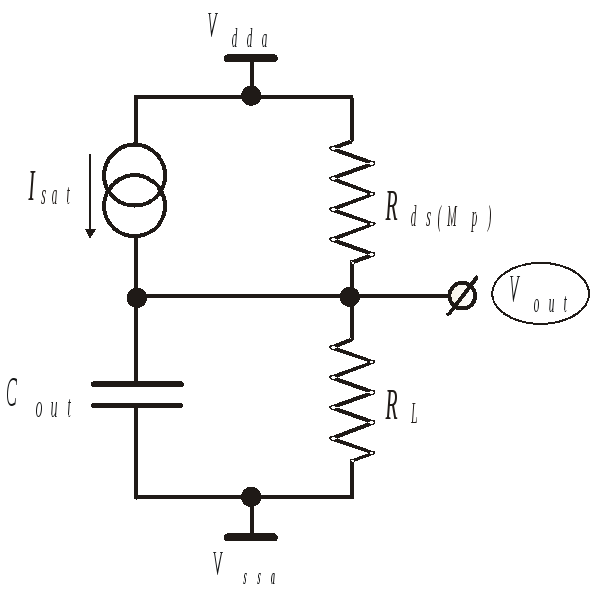
Рис. 3.9. Эквивалентная схема для расчета

переходного процесса в простейшем

усилителе с активной нагрузкой при отсечке

входного транзистора.

Переходной процесс в линейной системе, как известно, является экспоненциальным:

(3.30)

В выражении (3.30) параметр является начальным потенциалом, т.е. потенциалом на выходе усилителя в момент отрицательного скачка потенциала на затворе входного транзистора.

При относительно низком сопротивлении резистора некоторое увеличениеприведет к увеличению тока в, быстрому сравниванию его с токомв нагрузочном транзистореи установлению нового стационарного состояния, с новым, более высоким режимным потенциалом, при котором p-канальный транзистор еще находится в пологой области ВАХ.

Если сопротивление резистора нагрузки относительно высокое или резистор нагрузки вообще отсутствует, то, пока нагрузочный транзистор находится в пологой области ВАХ, ток, генерируемый этим транзистором, превышает токв резисторе нагрузки. Чем больше, тем меньше напряжение сток-истокв нагрузочном транзисторе. При достаточно высоком значениинапряжениестановится меньше граничного (равного, в свою очередь, превышению над порогом). Нагрузочный транзистор попадает в крутою область, ток в нем уменьшается и, при некотором значении напряжения сток-исток, при которомстановится равным, достигается стационарное состояние.

До тех пор, пока нагрузочный p-канальный транзистор еще не попадает в крутую область ВАХ, выходное напряжение определяется в основном не сопротивлением, а постоянной составляющей режимного тока, где– ток насыщения в рамках моделиLevel1, считающийся граничным током перехода между пологой и крутой областями ВАХ.. При этом скорость увеличения потенциалаот начального потенциаладо границыперехода p-канального нагрузочного транзистора в крутой режим определяется в основном процессом заряда емкостипостоянным током насыщения в пологой области:

(3.31)

Знак приблизительного равенства в (3.31) означает то, что, согласно (3.17) и приведенному выше, ток нагрузочного транзистора, являющийся режимным током, определяется не только граничным током , но также и сопротивлением. Проведем сравнение токаи максимального приращения токав резисторево время переходного процесса от потенциаладо потенциала. Максимальное приращение тока нагрузочного транзистора в пологой области определяется выражением:

(3.32)

Отношение кравно

(3.33)

Типовые значения параметров, входящих в (3.33) следующие:

; . Если при этом учесть, что реальный вклад максимальной добавкив суммарный режимный ток в переходном процессе длится весьма короткий промежуток времени, то погрешность выражения (3.31) составляет лишь около 10%. Поэтому, в связи с простотой выражения (3.31), именно оно при аналогичных условиях будет в дальнейшем применяться в аналитических оценках.

Предположим теперь, что на затвор входного транзистора подан положительный скачок потенциала с условием (как было показано выше, обеспечение достаточно высокого коэффициента усиления требует низких значений параметра и, следовательно, «большой» входной сигнал может быть весьма малым по сравнению с напряжением питания). Предположим далее, что абсолютная величина положительного скачка равна величине рассмотренного выше отрицательного. При этом условии и ввиду квадратичных характеристик МДП транзистора, ток во входном транзисторе, отводящий ток от нагрузки к отрицательному питанию, возрастает в 4 (четыре) раза. Скорость изменения потенциала выходного узла определяется разностью токов, подходящего от положительного питания и уходящего в отрицательное, поэтому в нашем случае, при подаче «большого» сигнала, равногои несоизмеримо меньшего, эта разность приблизительно в 3 (три) раза больше тока нагрузочного транзистора.

Итак, можно сделать выводы:

– при подаче на входе каскада с общим истоком относительно небольшого потенциала в добавление к режимному, увеличивающего ток во входном транзисторе, выходной узел разряжается со скоростью, значительно превышающей скорость заряда через нагрузочный элемент;

– подробному анализу в большинстве случаев подлежит лишь относительно медленный процесс перезарядки выходного узла нагрузочным элементом.