4.3.3. Передаточная функция двухкаскадного усилителя

Определим малосигнальную передаточную функцию двухкаскадного усилителя, используя эквивалентную схему на рис. 4.6. Для краткости записи здесь и далее по умолчанию:

(А) опускаем знак «~» над символом напряжения или тока: и;

(В) опускаем обозначение зависимости параметра от :и).

Ниже приводится система уравнений Кирхгофа.

(1) (4.33а)

(2) (4.33b)

Передаточная функция:

(4.34)

Учитываем, что , и в знаменателе выражения (4.34) пренебрегаем членами при параметре, не содержащими коэффициента:

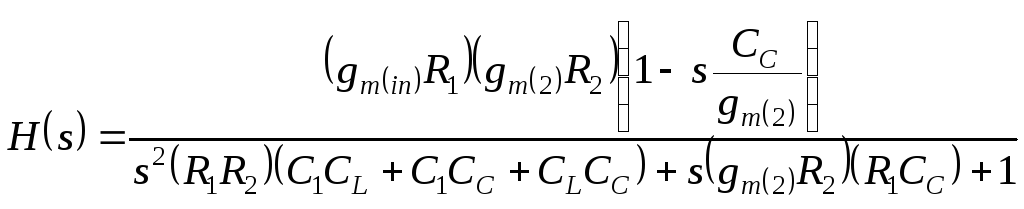(4.35)

Представим в (4.35) знаменатель в каноническом виде:

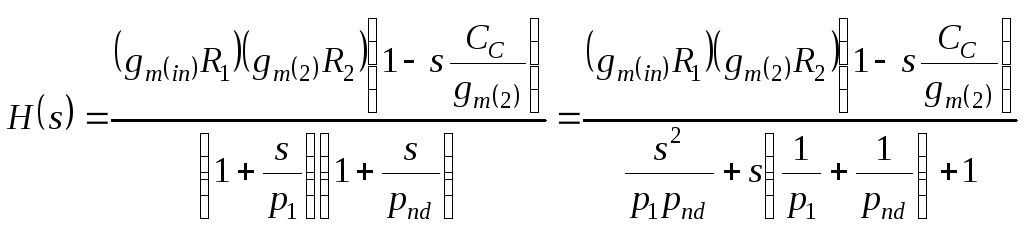(4.36)

Поскольку , выражение (4.36) можно представить в виде:

(4.37)

Сравнивая в (4.35) и (4.37) коэффициенты при одинаковых степенях , легко получить абсолютные величины полюсов(основной полюс) и(неосновной полюс), а также нуля(неосновной нуль, т.е. с собственной частотой,большей частоты единичного усиления: ). Имеем в виду, чтостационарное состояние системы возможно при нахождении действительных полюсов в отрицательной полуплоскости параметра ; нуль же стационарной системы может быть в обоих полуплоскостях, но система с нулем в положительной полуплоскости являетсянеминимальнофазовой. Итак:

(4.38а)

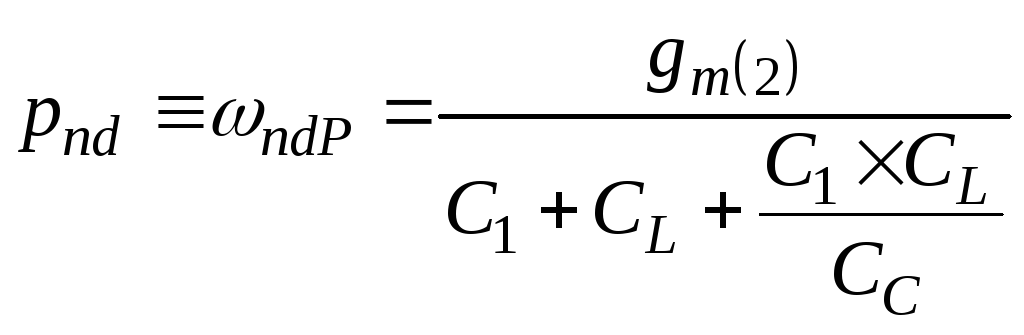(4.38b)

(4.38с)

Итак, схема двух каскадного усилителя является неминимальнофазовой, поскольку второй усилительный каскад охвачен отрицательной обратной связью только посредством конденсатора. Очевидная причина дополнительного фазового сдвига заключается в превращении на достаточно высокой частоте второго каскада совместно с в обратной связи вдиод, что изображено на рис. 4.6. Диод является неинвертирующей пассивной нагрузкой для первого каскада. Отсутствие инверсии сигнала при этом означает появление дополнительного сдвига фаз, за счет которого общий сдвиг фазы в усилителе становится больше 180º. Последнее, разумеется, недопустимо.

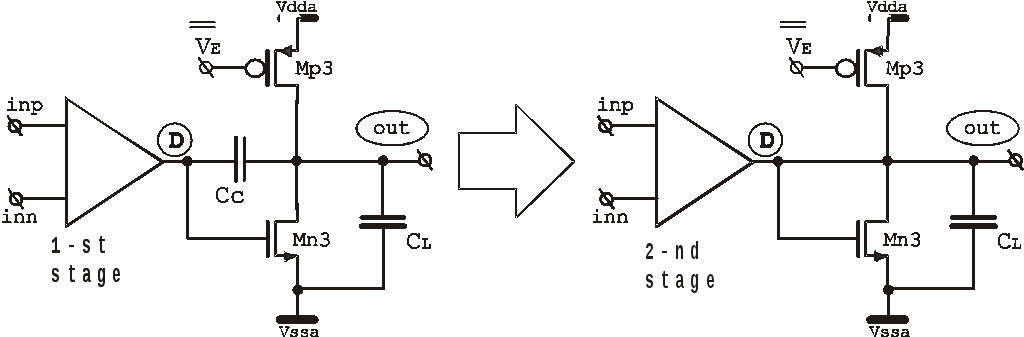
Рис. 4.6.Преобразование второго каскада на достаточно больших частотах из усилительного в пассивную диодную нагрузку.

4.3.4. Соотношение частот неосновного полюса, нуля и частоты единичного усиления

Из изложенного в следующем разделе следует, что частота единичного усиления двухкаскадного усилителя определяется выражением . Отсюда следует, что параметрыиодинаково, т.е.обратно зависят от . Поэтому, если, то. Соответствующая нежелательная АЧХ двухкаскадного усилителя, при которой на достатояно высоких частотах второй каскад является пассивной нагрузкой с соответствующим поворотом фазы на 180º приведена на рис. 4.7. При этом общий коэффициент усиления усилителя равен, и присуществуют условия для, большего единицы коэффициента усиления при сдвиге фазы в усилителе, большем 180º . Отсюда следует, что в любом случае должно выполняться неравенство, что обеспечит соотношенияи.

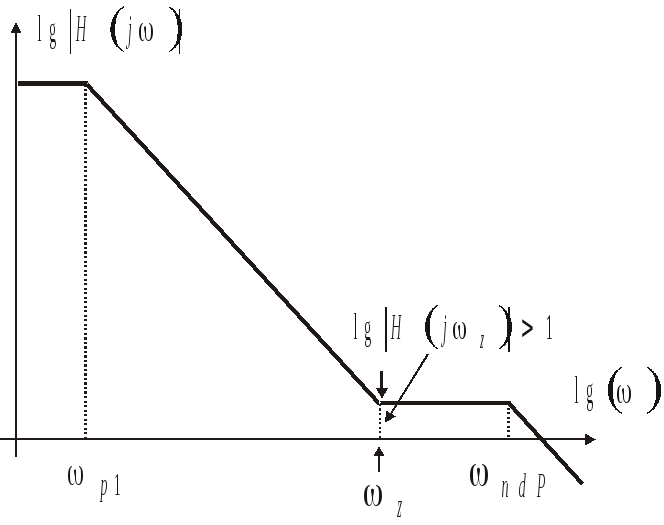
Рис. 4.7. АЧХ двухкаскадного ОИТУН при неблагоприятном сочетании значений параметров: ,и

Рассмотрим соотношение частоты неосновного полюса и частоты единичного усиления. Для того, чтобы сдвиг фазы под их влиянием в области частотбыл как можно меньше, собственная частотанеосновного полюса должна в возможно большей степени превышать(см. предыдущие главы). Надежным методом обеспечения этого условия, согласно (4.38b), как минимум, является соотношение или даже, поскольку влюбом случае частота единичного усиления прямо зависит от . 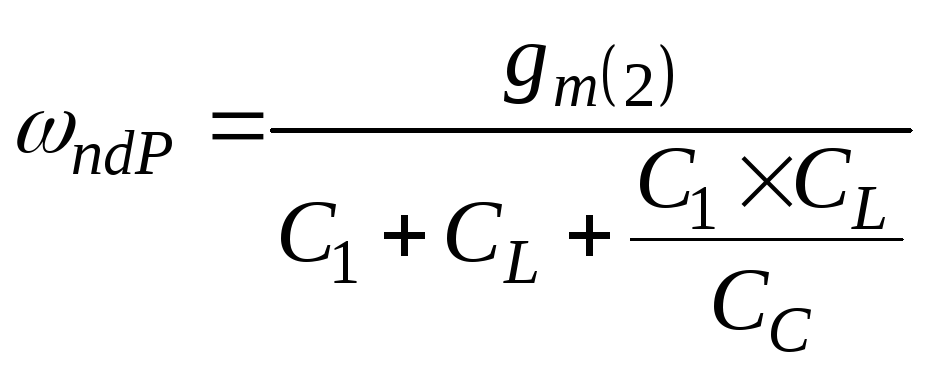Отметим с оптимизмом, однако, что если, и одновременно частота неосновного полюса больше частоты единичного усиления, т.е., то, имея в виду соотношения и , а также то, что практически всегда, можно утверждать, что также практически всегдабольшеи тем более больше. Такое сочетание значений параметров является благоприятным, поскольку «полочка» на АЧХ придется на интервал частот с.

В выражении (4.38b) для частоты неосновного полюса присутствует некоторый резерв увеличенияс помощью увеличения, однако, во – первых, этот резерв небольшой, во – вторых, увеличениенапрямую уменьшает частоту нуля и, в – третьих, увеличениеуменьшает скорость изменения выходного напряжения в режиме большого сигнала. Опыт проектирования двухкаскадных ОИТУН показывает, что наиболее надежным способом увеличенияявляется увеличение.