Содержание

1. Введение в анализ и синтез базовых узлов линейной обработки

аналоговых сигналов 6

1. Преобразование Лапласа как метод анализа линейных схем 7

2. Примеры расчета передаточных функций некоторых пассивных линейных схем 9

   1. Пассивный RC фильтр низких частот первого порядка 10

   2. Простейший пассивный RLC фильтр низких частот 12

3. Примеры расчета передаточных функций простейших активных линейных схем аналоговой обработки сигналов 14

   1. Неинвертирующий усилитель 14

   2. Инвертирующий усилитель 15

   3. Активный инвертирующий интегратор 16

4. Введение в реализацию ARC биквада 17

   1. Принцип масштабирования пассивных элементов в ARC фильтрах 20

5. Введение в концепцию переключаемых конденсаторов 21

   1. Неинвертирующий переключаемый конденсатор с задержкой, чувствительный к паразитным емкостям 21

   2. Неинвертирующий переключаемый конденсатор без задержки, не чувствительный к паразитным емкостям 25

   3. Инвертирующий ПК интегратор без задержки, не чувствительный к паразитным емкостям 28

   4. Инвертирующий переключаемый конденсатор с задержкой, не чувствительный к паразитным емкостям 31

   5. Неинвертирующий ПК интегратор с задержкой 34

6. Реализация биквада на базе переключаемых конденсаторах прямой заменой резисторов на переключаемые конденсаторы 36

7. Дискретизация аналогового сигнала. Идеальные выборки и z-преобразование 39

   1. Передаточная функция ПК интегратора без задержки 42

   2. Передаточная функция ПК интегратора с задержкой 43

1. Модели элементов интегральных схем 44

   1. Модели пассивных компонентов ИМС 45

      1. Модель полупроводниковых диодов 45

      2. Модель резисторов 47

   2. Модель МДП транзистора 49

      1. Нелинейная модель МДП транзистора 49

      2. Малосигнальная модель МДП транзистора 53

2. Базовые элементы КМДП операционных усилителей 55

   1. Простейший усилитель напряжения с общим истоком 55

      1. Простейший усилительный каскад с общим истоком и активной нагрузкой 59

      2. Малосигнальные характеристики простейшего КМДП усилителя с активной нагрузкой 63

      3. Частота единичного усиления простейшего усилителя 73

      4. Соотношение малосигнальных параметров простейшего 73

      5. Простейший усилитель в режиме большого сигнала74

      6. Расчет выходного сопротивления 79

      7. Элементарный анализ величины входной емкости. Емкость Миллера 80

      8. Пример топологии простейшего усилителя 83

   2. Выходное сопротивление и коэффициент передачи каскада с диодом в нагрузке 87

      1. Передаточная характеристика каскада с общим истоком и с диодной нагрузкой 91

   3. Токовое зеркало 91

      1. Формирование режимных потенциалов в простейшем усилителе с общим истоком 94

   4. Истоковый повторитель 96

      1. Выходное сопротивление и входная емкость истокового 97

   5. Метод увеличения выходного сопротивления усилителя 99

   6. Каскодный усилитель 105

      1. Передаточная функция простейшего каскодного усилителя с идеальной токовой нагрузкой 107

      2. Роль емкости в выходном узле каскодного усилителя 112

      3. Диапазон изменения выходного напряжения 115

      4. Схемы формирования постоянного смещения на затворе каскодного транзистора 117

      5. Каскодное токовое зеркало 119

      6. Самосмещаемое каскодное токовое зеркало 120

   7. Концепция активного каскодного транзистора (материал для дополнительного изучения подготовленными студентами с использованием периодической литературы) 121

   8. Дифференциальный каскад 124

      1. Допустимый диапазон входного синфазного напряжения 127

      2. Дифференциальный каскад как источник тока, управляемый входным напряжением. Несимметричный и симметричный входные сигналы 128

3. Архитектуры КМДП операционных усилителей 133

   1. Методика оценки малосигнальных характеристик операционного усилителя 133

      1. Методика замены нескольких действительных неосновных полюсов в передаточной функции операционного усилителя одним «эффективным» неосновным полюсом 137

      2. . Расчет запаса фазы операционного усилителя с действительными полюсами 139

   2. Однокаскадные операционные усилители как операционные источники тока, управляемые напряжением (ОИТУН) 140

      1. «Телескопический» ОИТУН 140

         1. Базовые характеристики «телескопического» ОИТУН 141

         2. Упрощенная методика расчета фазы в «телескопическом» усилителе 143

         3. Оценка частот неосновных полюсов «телескопического» ОИТУН 144

         4. Анализ переходных процессов 145

      2. «Согнутый» каскодный ОИТУН с р-канальным входом 147

         1. Диапазоны входного синфазного и выходного напряжений 149

         2. Режим малого сигнала 149

         3. Переходной процесс в режиме большого сигнала 150

      3. «Согнутый» каскодный ОИТУН с n-канальным входом 150

   3. Двухкаскадный операционный усилитель (ОИТУН) 151

      1. Базовая схема двухкаскадного ОИТУН 151

      2. Эквивалентная малосигнальная схема двухкаскадного усилителя 153

      3. Передаточная функция двухкаскадного усилителя 155

      4. Соотношение частот неосновного полюса, нуля и частоты единичного усиления 157

      5. Частота единичного усиления двухкаскадного ОИТУН 158

      6. Устранение нуля в положительной полуплоскости 160

      7. Реакция двухкаскадного ОИТУН на большой входной сигнал 164

      8. Реакция двухкаскадного ОИТУН на большой синусоидальный сигнал 167

      9. Распространенная архитектура двухкаскадного ОИТУН 168

4. Шум и его анализ в КМДП аналоговых ИМС 169

   1. Основные определения 170

      1. Cуммирование шумов 171

      2. Анализ шума в частотной области 173

      3. Белый шум 174

      4. Полоса шума 175

   2. Пример расчета шума ARC фильтра первого порядка 177

      1. Реакция на шумовой источник тока 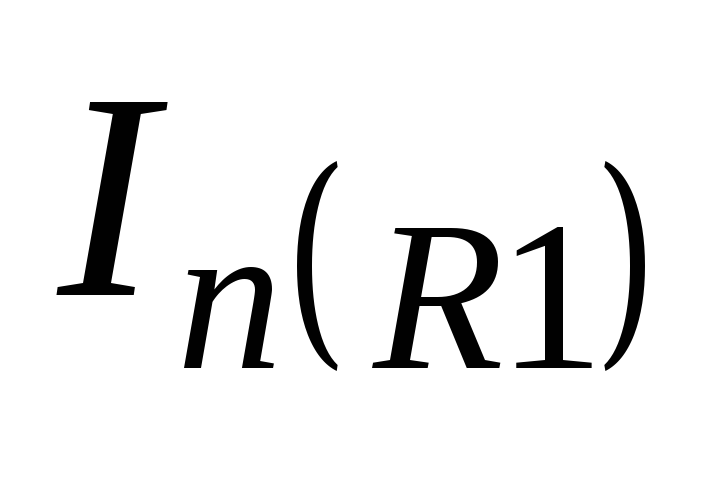179

      2. Реакция на шумовой источник тока 180

      3. Реакция на шумовой источник напряжения 180

   3. Пример расчета приведенного ко входу шума КМДП дифференциального каскада с активной нагрузкой 181

   4. Приведенный ко входу собственный «белый» шум повторителя напряжения 186

   5. Собственный шум многокаскадного усилителя 187

   6. Шум каскодного усилителя 188

5. Полностью дифференциальные ОИТУН 189

   1. Базовая архитектура полностью дифференциальных схем 189

   2. Принципиальные преимущества полностью дифференциальных схем 191

      1. Зависимость потенциала общего истока дифкаскада от сигнала 193

   3. Принципиальные недостатки полностью дифференциальных схем 195

   4. Варианты непрерывных во времени схем синфазной обратной связи (СОС) 196

      1. Схема с ограниченным диапазоном входных сигналов 196

      2. Непрерывная во времени cхема СОС с максимальным диапазоном входных сигналов 199

      3. Варианты схем синфазной обратной связи на базе переключаемых конденсаторов 201

1. Введение в анализ и синтез базовых узлов линейной обработки

аналоговых сигналов

1.1. Преобразование Лапласа как метод анализа линейных схем

В рамках настоящего пособия «Основы схемотехники дискретно-аналоговых ИМС» рассматриваются схемотехника и методы исследования линейных КМДП дискретно-аналоговых интегральных схем. Как известно, все множество параметров линейной схемы по определению не зависит от уровня (величины, амплитуды) входного по отношению к схеме сигнала . По этой причине взаимосвязь входногои выходногосигналов может быть выраженалинейной функцией.

Если сигналы рассматриваются во временной области, то используется импульсная характеристика (функция) в сочетании с интегралом Дюамеля («свертки»). Если известны входной сигнал и импульсная характеристикалинейной схемы, то сигнална выходе схемы определяется из следующего выражения [1 – 4]:

(1.1)

Другим общепризнанным методом анализа линейных схем является спектральный метод . В рамках этого метода в теории связи наибольшее распространение получил метод преобразование Лапласа [1 – 4], которое:

– в отличие от преобразования Фурье, не ограничено использованием только сигналов, описываемых абсолютно интегрируемыми функциями;

– позволяет решать линейные интегро-дифференциальные уравнения методами алгебры;

– в отличие от анализа во временнòй области позволяет не только описывать нестационарные (переходные) процессы, но также получать и анализировать стационарные амплитудно-частотные и фазочастотные особенности.

Исчерпывающей характеристикой линейной схемы в спектральном методе является передаточная функция , специфическая для каждой системы. При подаче на вход линейной системы сигнала, сигнална выходе находится следующим образом:

(А) определяется ИЗОБРАЖЕНИЕ входного сигналана комплексной плоскости:

(1.2)

(В) изображение входного сигнала умножается на передаточную функциюсистемы, в результате чего получается изображениесигнала на выходе линейной системы:

(1.3)

(С) из изображения сигнала на выходе определяется ОРИГИНАЛвыходного сигнала:

(1.4)

Интегрирование в выражении (1.4) производится в комплексной плоскости вдоль прямой, проходящей параллельно мнимой оси на расстоянииот последней и замыкается вдоль дуги бесконечно большого радиуса, образовывая замкнутый контур интегрирования. При этомвнутри контура должны находиться все полюсы подынтегральной функции, и значение в этом случае равно сумме вычетов в полюсах подынтегральной функции.

При подаче сигнала на вход системы вначале возникает нестационарный процесс установления нового состояния (переходной процесс), и действительная часть комплексной переменнойвходит в показатели экспонент, определяющих затухающий (при) или возрастающий (при) характер переходного процесса. После затухания переходного процесса система либо остается в покое, либо остаются тольковынужденные процессы (как правило, колебания), обусловленные колебаниями входного сигнала. Если следы нестационарности процесса исчезли, можно считать, что во все последующее время , и. В этом случае (в новом стационарном состоянии) выражения (1.2) – (1.4) представляют собой преобразования Фурье, являющемся частным случаем преобразования Лапласа. Модуль полученного комплексного выражения представляет зависимость от частоты модуля коэффициента передачи (усиления) системы, а фаза представляет зависимость от частоты фазы входного синусоидального сигнала.

Основные свойства преобразования Лапласа

Пусть функция является оригиналом, а– изображением функции, т.е.. Тогда из (1.2) – (1.4) можно получить основные свойства преобразования Лапласа.

Таблица 1.1

Таблица некоторых преобразований Лапласа

Таблица 1.2