Вариант 92
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Решите неравенство (114 )x ≥ |
4 |
. |
|
|
|
|
11 |
|
|
А) (–∞; –1]; |
Б) [–1; +∞); |
|
В) (–∞; 1]; |
Г) [1; +∞). |
|
|
|
|
|
|
|
3 |
1 |
|
1.2. Представьте в виде степени выражение b4 |
:b3 . |
|
5 |
|
1 |
|
|
9 |
|
|
13 |
А) b |
12 |
; |
Б) b |
4 |
; |
|
В) b |
4 |
; |
|
Г) b12 . |
1.3. Найдите координаты точки |
пересечения |
графиков |
функций y = lgx |
и y = 3. |
|
|
|
|
|
|
|
|
|
|
А) (30; 3); |
Б) (10; 3); |
|
В) (3; 1000); |
Г) (1000; 3). |
1.4. Сколько корней имеет уравнение sin x = sin2 ? |
|
А) ни одного корня; |
|
В) два корня; |
|
Б) один корень; |
|
|
|
|
|
Г) бесконечно много корней. |
1.5.Найдите процентное содержание железа в руде, если 600 кг руды содержат 54 кг железа.
А) 7 %; |
|
|
Б) 8 %; |
В) 9 %; |
|
Г) 10 %. |
1.6. Упростите выражение ctg(2π+α)ctg(32π −α) |
|
|
|
. |
А) ctg2α ; |
|
|
Б) tg2α ; |
В) 1; |
|
Г) –1. |
1.7. Найдите производную функции |
f (x) = |
|
4x −1 . |
|
|
|
|
|
А) f '(x) = |
2 |
1 |
|
|
; |
В) f '(x) = |
1 |
−1 |
; |
|
|
|
|
|
4x −1 |
|
|
|
|
4x |
|
|
|
Б) f '(x) = |
|
2 |
|
; |
|
Г) f '(x) = |
4 |
. |
|
|
|
|
|
|
4x −1 |
|
|
|
|
|
4x |
−1 |
|
|
|
1.8. Какое число является решением неравенства sin(3x − π6)> 12 ? |
А) |
π |
; |
|
|
Б) 0; |
В) |
π |
; |
|
Г) |
π |
. |
|
|
|
3 |
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1.9.Найдите разность арифметической прогрессии, первый член которой равен –32, а девятый член равен 40.
А) 8; |
Б) 9; |
В) –8; |
Г) –9. |
1.10. Укажите область определения функции y = arccos(x +2) .
А) (–3; –1); |
Б) (1; 3); |
В) [–3; –1]; |
Г) [1; 3]. |
1.11. Упростите выражение ( |
15 − 4)2 + ( 15 + 4)2 . |
|
А) 8; |
Б) 2 15 ; |
В) –2 15 ; |
Г) 8+ 2 15 . |
1.12. Сколько нечетных пятизначных чисел, все цифры которых различны, можно записать, используя цифры 1, 2, 3, 4 и 5?
А) 16; |
Б) 24; |
В) 48; |
Г) 72. |
1.13. Острый угол равнобокой трапеции в 3 раза меньше ее тупого угла. Найдите эти углы.
А) 40°; 120°; |
Б) 45°; 135°; |
В) 50°; 150°; |
1.14. Чему равен периметр треугольника ABC, |
изображенного |
на |
рисунке, |
вписанного |
в полуокружность, |
радиус которой ра- |
вен R, если α = 45° ? |
|
А) 4R; |
|
В) 4R 2 ; |
A |
|
|
Б)2R ( 2 +1); |
|
Г) найти невозможно. |
Г) 48°; 144°.
B
 α C
α C
1.15. Вычислите объем правильной треугольной призмы, сторона основания которой равна 4 см, а боковое ребро — 12 см.
А) 12 3 см3; |
Б) 16 3 см3; |
В) 24 3 см3; |
Г) 48 3 см3. |
1.16. Центр какой из окружностей принадлежит оси абсцисс?
А) (x − 4)2 + (y − 4)2 = 2; |
В) (x − 4)2 + y2 = 2; |
Б) (x + 4)2 + (y + 4)2 = 2 ; |
Г) x2 + (y − 4)2 = 2. |
Вариант 93
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Какая функция является возрастающей?
А) y = 0,1x ; Б) y =10x ; В) y =10 ;
1.2. График какой функции изображен на рисунке?
А) y = x2 +3; |
В) |
y = −x2 +3; |
Б) y = x2 −3; |
Г) |
y = −x2 −3. |
1.3.Вычислите значение выражения cos52°cos38°−sin52°sin38°.
1.4.Сравните 3 2 и 9.
А) 3 2 < 9; Б) 3 2 = 9;
Г) 0.
В) 3 2 > 9;
Г) сравнить невозможно.
1.5.Областью определения какой из функций является множество действительных чисел?
А) y = lg| x |; |
|
|
|
В) |
y = log |
x |
2 (x2 +2) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б) y = 4 | x | ; |
|
|
|
Г) |
y = |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
2 |
+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
lg(x |
|
|
|
|
|
|
1.6. Какое неравенство не имеет решений? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) cosx ≥1; |
|
Б) cosx >1; |
В) |
cosx <1; |
|
|
Г) |
cosx ≤1. |
1.7. Найдите производную функции |
f (x) = |
3x |
|
. |
|
|
|
|
|
|
|
x −5 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
6x −15 |
|
|
|
|
А) f '(x) = − |
|
; |
|
В) f '(x) = |
|
|
|
; |
|
|
(x −5)2 |
|
(x −5)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б) f '(x) = |
|
15 |
; |
|
|
Г) f '(x) = |
|
15−6x |
. |
|
|
(x −5)2 |
|
|
(x −5)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.8. Вычислите интеграл ∫x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
А) 6; |
|
|
Б) 6,2; |
|
В) 6,6; |
|
|
|
|
|
|
|
|
Г) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
203 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.9. Упростите выражение 5 b2 |
b . |
|
А) 7 b3 ; |
Б) 7 b5 ; |
В) b ; |
Г) 5 b4 . |
1.10. Из полного комплекта шахматных фигур наугад вынимают одну фигуру. Какая вероятность того, что эта фигура будет черной пешкой?
|
А) |
|
1 |
; |
Б) |
1 |
; |
В) |
1 |
; |
Г) |
1 . |
|
16 |
|
|
|
|
8 |
|
|
4 |
|
|
2 |
|
1.11. Решите неравенство |
x −6 |
≤ 0 . |
|
|
|
|
|
x2 −6x +9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) (–∞; 6); |
|
Б) (–∞; 6]; |
В) |
(−∞;3) (3; 6) ; |
Г) |
(−∞;3) (3; 6]. |
|
1.12. На рисунке |
изображен |
график функции |
|
y |
|
|
|
|
|
|
|
|
y = f (x) , |
определенной |
на |
промежутке |
|
|
|
|
|
[–3; 3]. Сколько корней |
имеет |
уравнение |
|
1 |
|
|
|
lg f (x) = 0? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) ни одного корня; |
|
3 |
|
0 |
1 |
3 |
x |
Б) один корень; |
|
|
|
|
|
|
|
В) два корня; |
|
|
|
|
|
|
|
|
Г) три корня. |
|
|
|
|
|
|
|
|
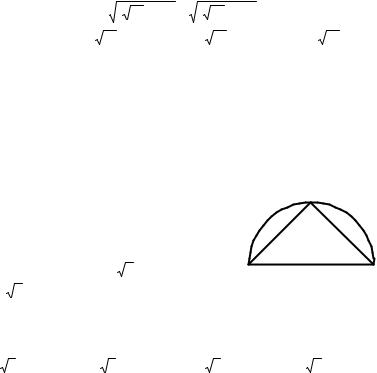
1.13. На рисунке изображены |
окружность |
с центром O |
и |
правильный треуголь- |
ник OAB. Найдите угол α. |
|
|
А) 150°; Б) 135°; В) 120°; Г) 90°. |
|
1.14. Вычислите |
площадь треугольника, |
две |
стороны которого |
равны 5 |
3 см и |
8 см, |
а угол между ними — 60°. |
|
|
А) 60 3 см2; |
Б) 60 см2; |
В) 30 см2; |
A
O α
B
Г) 30 3 см2.
3 см2.
1.15.Найдите отношение объемов двух шаров, радиусы которых равны 3 см
и6 см.
А) 1 : 3; |
Б) 1 : 8; |
В) 1 : 2; |
Г) 1 : 4. |
1.16. При каком |
значении k |
векторы m (2; –3; k) |
и n (k; 4; 2) перпен- |
дикулярны? |
|
|
|
А) 3; |
Б) –3; |
В) 4; |
Г) –4. |
Вариант 94
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1.Упростите выражение b34 8 .
А) b5 ; |
|
|
|
Б) b6 ; |
В) b20 ; |
Г) b7 . |
1.2. Чему равно значение выражения sin(arcsin 12 +arccos12)? |
|
|
|
А) 0; |
|
|
|
Б) 12 ; |
В) 1; |
Г) |
3 |
. |
|
|
|
2 |
|
1.3. Решите неравенство |
3x ≥ 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) [1; +∞); |
Б) [–1; +∞); |
В) (–∞; 1]; |
Г) (–∞; –1]. |
1.4. Сократите дробь |
|
|
x −16 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x +4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
А) |
x + 4; |
Б) |
x −4 ; |
В) 4 x + 4; |
Г) 4 x −4 . |
1.5. Какая функция является обратной к функции y = log2 x ? |
|
|
|
А) y = 2x ; |
Б) y = x2 ; |
В) y = |
2 |
; |
|
|
|
Г) y = x . |
x |
1.6. Какое неравенство не имеет решений? |
|
|
|
|
π |
|
|
|
|
|
|
А) arcsin x > 0; |
|
|
|
|
|
|
В) |
sinx < |
; |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Б) arcsin x < 0; |
|
|
|
|
|
|
Г) |
sinx > |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1.7. Найдите производную функции |
f (x) = cos4−e3 . |
|
|
|
|
|
А) |
f '(x) = −sin4−e3 ; |
В) |
f '(x) =1; |
|
|
|
|
|
Б) f '(x) = −3e2 ; |
|
|
|
|
|
|
Г) f '(x) = 0 . |
|
|
|
|
|
1.8. Какая функция является первообразной функции |
f (x) = x6 ? |
А) |
F(x) |
= |
x7 |
; |
Б) |
F(x) = |
x7 |
; |
В) F(x) = 6x5 ; |
Г) F(x) = x7 . |
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.9. Найдите |
разность |
арифметической |
прогрессии |
(xn ), |
если x6 = −3, |
x16 =12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
А) 1,5; |
|
|
|
Б) |
0,9; |
|
|
|
В) 1; |
Г) 1 |
. |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

1.10. Фирма |
приобрела некоторый |
товар за |
7000 грн и продала его за |
9450 грн. Сколько процентов составила прибыль фирмы? |
А) 25 %; |
Б) 35 %; |
В) 40 %; |
Г) 70 %. |
1.11. Учащихся одиннадцатого класса с углубленным изучением математики опросили: какой школьный предмет они будут сдавать во время Государственной итоговой аттестации, кроме двух обязательных (украинский язык и математика). Были получены такие данные:
|
Название |
|
Физи- |
Химия |
Геогра- |
Иностран- |
Информа- |
|
предмета |
|
ка |
|
фия |
ный язык |
|
тика |
|
Количество |
|
10 |
3 |
4 |
6 |
|
7 |
|
учащихся |
|
|
|
|
|
|
|
|
|
|
|
Чему равна мода полученных данных? |
|
|
|
|
А) 10 учащихся; |
|
В) физика; |
|
|
|
|
Б) 6 учащихся; |
|
|
Г) иностранный язык. |
|
1.12. Решите неравенство (x +1)(4− x)(x −7)2 < 0 . |
|
|
|
|
А) (−∞; −1] [4; 7) (7; +∞) ; |
В) (−∞; −1] [4; +∞); |
|
|
Б) (−∞; −1) (4; 7) (7; +∞) ; |
Г) (−∞; −1) (4; +∞) . |
|
1.13. Дано: ∆DFK |
и ∆BNT , D = B, F = N, DK=24 см, |
BT=4 см, |
|
NT=6 см. Найдите сторону FK. |
|
|
|
|
|
А) 16 см; |
Б) 24 см; |
В) 36 см; |
Г) 32 см. |
|
1.14. Вычислите площадь параллелограмма, две стороны которого равны 4 см и 5 3 см, а угол между ними — 60°.
3 см, а угол между ними — 60°.
А) 10 3 см2; |
Б) 20 3 см2; |
В) 15 см2; |
Г) 30 см2. |
1.15. В шаре с центром O, изображенном на рисун- |
|
ке, проведено сечение с центром O1 на расстоя- |
|
нии 5 см от центра шара. Найдите радиус сече- |
|
ния, если радиус шара равен 13 см. |
|
O |
А) 4 см; |
|
В) 12 см; |
|
|
|
|
Б) 6 см; |
|
Г) 10 см. |
|
|
A |
O1 |
1.16. Известно, что вектор b |
равен сумме векторов |
|
|
|
|
и |
|
Найдите |
координаты |
вектора |
если |
M(4;–3;2), |
MN |
NK . |
b , |
K(2;1;–1), N — некоторая точка пространства.
А) b |
(–2; 4; –3); |
В) b (3; –1; 0,5); |
Б) b |
(6; –2; 1); |
Г) найти невозможно. |
Вариант 95
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
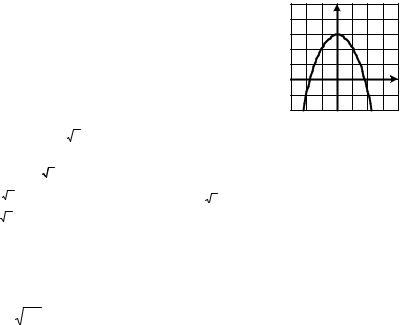
1.1. График какой функции изображен на ри- y сунке?
сунке?
А) y = x2 ; |
В) y = −x2 ; |
|
|
|
Б) y = x ; |
Г) y = − x . |
|
|
|
1.2. Найдите координаты точки пересечения гра- |
1 |
|
|
фика функции |
y = log2(x2 − 3x +8) с осью |
|
|
|
0 1 |
x |
ординат. |
|
|
|
|
|
А) (0; 8); |
Б) (0;3); |
В) (3; 0); |
Г) (8; 0). |
|
|
1.3. Областью определения какой из функций является промежуток (–∞; 10)?
|
А) y = 6 x −10 ; |
Б) y = |
|
|
|
1 |
|
; В) y = 6 −x +10 ; |
Г) y = |
|
1 |
. |
|
6 x −10 |
6 −x +10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Упростите выражение |
|
|
tg5α−tg2α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ tg5αtg2α |
|
|
|
|
|
|
|
|
|
А) ctg7α; |
|
|
|
Б) ctg3α; |
|
|
|
В) tg7α; |
|
|
Г) tg3α. |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5. Сократите дробь |
a4 −36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a8 −6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
А) a 8 −6 ; |
Б) a 8 |
+6 |
; |
|
|
В) a |
4 |
+ |
6; |
Г) a |
4 |
|
−6. |
|
|
1.6. Найдите производную функции |
f (x) = 4log6 x . |
|
|
|
|
|
|
|
А) f '(x) = |
|
4 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
В) f '(x) |
= |
4 ; |
|
|
|
|
|
|
|
x ln6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
Б) f '(x) = |
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
Г) f '(x) |
= |
1 . |
|
|
|
|
|
|
|
x ln6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.7. Вычислите интеграл ∫3 |
|
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) 3 ; |
|
|
|
Б) − |
3 |
; |
|
|
|
В) 233 ; |
|
Г) – 233 . |
|
|
|
|
|
3 |
|
|
|
|
|
1.8.Найдите знаменатель бесконечной геометрической прогрессии, первый член которой равен –8, а сумма равна –6.
А) |
−1 |
; |
Б) |
1 |
; |
В) |
−1 |
; |
Г) |
1 . |
|
3 |
|
|
3 |
|
|
4 |
|
|
4 |
1.9.В таблице приведены данные о посещении художественной выставки
втечение недели:
День недели |
Поне- |
Втор- |
Среда |
Чет- |
Пят- |
|
Суб- |
Воскре- |
|
дельник |
ник |
|
верг |
ница |
|
бота |
сенье |
Количество |
120 |
200 |
210 |
180 |
300 |
|
440 |
410 |
посетителей |
|
|
|
|
|
|
|
|
|
Чему равен размах данной выборки? |
|
|
|
|
|
А) 440 посетителей; |
|
В) 320 посетителей; |
|
|
Б) 210 посетителей; |
|
Г) 290 посетителей. |
|
|
1.10. Какоенаименьшеезначениепринимает функция f (x) = 25cos2 x+3sin2 x ?
А) 64; |
Б) 16; |
В) 2; |
Г) 8. |
1.11. Пять землекопов, работая с одинаковой производительностью труда, выкапывают 2 одинаковые траншеи за 8 ч. Сколько времени требуется одному землекопу, чтобы выкопать одну такую траншею?
А) 10 ч; |
Б) 15 ч; |
В) 20 ч; |
Г) 30 ч. |
1.12. Значение какого выражения делится нацело на 4 при всех нечетных натуральных значениях n?
А) n2 +1; |
Б) n2 −1; |
В) n3 +1; |
Г) n3 −1. |
1.13. Чему равен меньший из углов параллелограмма, если сумма двух из них равна 110°?
А) 55°; |
Б) 70°; |
В) 65°; |
Г) 50°. |
1.14. Найдите радиус окружности, вписанной в правильный треугольник со стороной 18 см.
А) 12 3 см; |
Б) 9 3 см; |
В) 6 3 см; |
Г) 3 3 см. |
1.15. Какое наименьшее количество граней может иметь пирамида?
А) 4 грани; |
Б) 5 граней; |
В) 6 граней; |
Г) 7 граней. |
1.16. Найдите модуль вектора bG (2; –2; 2).
А) 6; |
Б) 6 ; |
В) 2 3 ; |
Г) 2. |
208

Вариант 96
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
|
|
|
|
|
|
|
|
1 |
1 |
в виде степени. |
|
|
|
|
|
|
1.1. Представьте выражение a3 |
:a4 |
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
3 |
|
7 |
|
|
А) a |
12 |
; |
Б) a |
3 |
|
; |
|
В) a |
4 |
; |
Г) a |
12 |
. |
|
1.2. Решите неравенство (16)x ≤1. |
|
|
|
|
|
|
|
|
|
|
А) (–∞; 6]; |
Б) (–∞; 0]; |
|
В) [0; +∞); |
Г) (–∞; 1]. |
1.3. Значение какого выражения является натуральным числом? |
А) (12 3 2)3 ; |
Б) 4 (−10)4 ; |
В) |
5 −32 ; |
Г) |
( 2)2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1.4. Решите неравенство (4− x)cos2 ≤ 0. |
|
|
|
|
|
|
|
|
|
А) [4; +∞); |
Б) (–∞; 4]; |
|
В) (–∞; 4); |
Г) (4; +∞). |
1.5. Упростите выражение cosβcos5β+sinβsin5β. |
|
|
|
|
|
|
А) cos4β ; |
Б) cos6β; |
|
В) sin4β; |
Г) sin6β. |
1.6. Известно, что log5 6 = a . Чему равно значение выражения log6 25? |
А) |
a |
; |
Б) 2a ; |
|
В) a2 ; |
Г) |
2 |
. |
2 |
|
|
a |
1.7. Вычислите |
значение |
производной |
функции |
f (x) = 3−ex в точке |
x0 = ln3. |
|
|
|
|
|
|
|
|
|
Г) 3−e . |
А) 0; |
Б) –3; |
|
|
В) –6; |
1.8.Семья приобрела в кредит шкаф, сделав первый взнос в размере 256 грн, что составляет 16 % стоимости шкафа. Сколько гривен стоит шкаф?
|
|
|
|
|
|
|
А) 1000 грн; |
Б) 1200 грн; |
В) 1600 грн; |
|
Г) 2000 грн. |
1.9. Укажите область определения функции y = |
|
|
1 |
. |
2 |
−log2 x |
А) (0; 4) (4; +∞); |
В) (–∞; 4) |
(4; +∞); |
Б) (0; +∞); |
|
Г) (0; 4). |
|
|
|
1.10. В выборке, состоящей из 8 чисел, число 6 встречается 3 раза, число 7 — 4 раза, число 8 — 1 раз. Найдите среднее значение этой выборки.
А) 6,5; |
Б) 7; |
В) 6,75; |
Г) 6,25. |
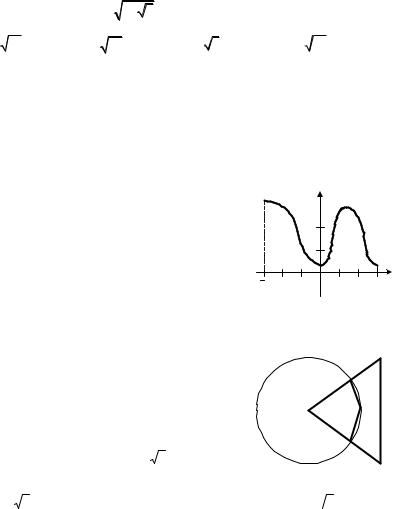
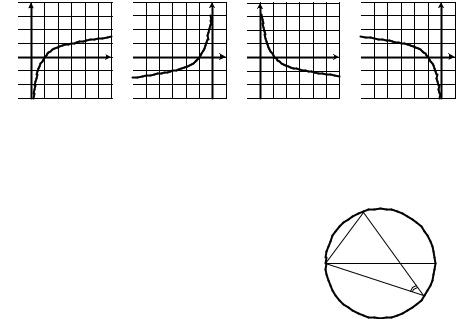
1.11. На одном из рисунков изображен график функции y = −log3(−x) . Укажите этот рисунок.
1.12. Функция y = f (x) определена на множестве действительных чисел.
Какое из данных значений функции является наименьшим, если функция f является убывающей?
А) f (12); Б) f (23); В) f (34); Г) f (56).
1.13. Отрезок AB — диаметр окружности, изображенной на рисунке, BAC = 50°. Чему
равен угол α?
А) 40°; Б) 50°; |
В) 60°; Г) 70°. |
1.14. В треугольнике |
ABC известно, что |
BC=24 см, sinB=0,3, sinA=0,8. Найдите сторону AC.
C
A  50° B
50° B
α
А) 64 см; |
Б) 12 см; |
В) 48 см; |
Г) 9 см. |
1.15. Чему равен объем цилиндра, радиус основания которого R, а высота равна радиусу основания?
А) 3πR3 ; |
Б) 2πR3 ; |
В) πR3 ; |
Г) 13πR3 . |
JJG
1.16. Найдите координаты вектора AB , если A(–3;2;–1), B(1;1;–2).
А) |
JJJG |
В) |
JJG |
AB (–2; 3; –3); |
AB (–2; 1; –3); |
Б) |
JJJG |
Г) |
JJG |
AB (4; –1; –1); |
AB (–4; 1; 1). |

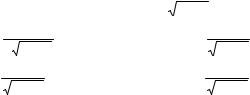






 α
α 
 3 см
3 см 3 см, а угол между ними — 60
3 см, а угол между ними — 60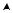 сунке?
сунке? 50°
50°