
ДПА-11-2014-2
.pdf
Вариант 35
Часть вторая
Решите задания 2.1 – 2.8. Запишите ответ в бланк ответов.
2.1. |
Найдите значение выражения ( 7−4 |
3 + 7+4 3)2 . |
2.2. |
Укажите область значений функции |
f (x) = 3sinx . |
2.3. Решите неравенство:
log1(x +4) > log1(x2 +2x −2) .
66
2.4.Решите уравнение cos2x + sinx = 0.
1 |
|
|
|
1 |
|
|
2.5. Вычислите интеграл ∫ |
2 |
− |
|
|
dx . |
|
x |
2 |
|||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2.6. Арифметическая прогрессия ( an) задана формулой общего члена an = 7−3n . Найдите сумму десяти первых членов прогрессии.
2.7. Периметр треугольника ABC, описанного около окружности, равен 36 см. Точка касания окружности со стороной BC делит ее в отношении 2:5, считая от точки B, а точка касания со стороной AC удалена от точки A на 4 см. Найдите сторону AB.
2.8.Ребро куба ABCDA1B1C1D1 равно 2 см. Чему равна площадь треугольника
ADC1?
Часть третья
Решение задач 3.1 – 3.3 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
3.1. Составьте уравнение |
|
касательной к графику функции |
|
f (x) = cos2 x |
|||
в точке с абсциссой x |
0 |
= |
π |
. |
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
||
3.2. Докажите тождество |
cos(2π+ α4)−sin(2π+ α4)ctg α8 |
= tg |
α |
|
|||
cos(72π − α4)+cos(α4 −3π)ctg α8 |
8 |
||||||
3.3.Через сторону правильного треугольника проведена плоскость, образующая с плоскостью треугольника угол 30°. Найдите углы, которые образуют две другие стороны треугольника с этой плоскостью.
71
Часть четвертая
Решение задач 4.1 – 4.4 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
4.1.м Решите неравенство:
6+ x − x2 |
≥ |
6+ x − x2 |
|
|
2x +5 |
x + 4 |
|||
|
|
4.2.м При каких значениях параметра a уравнение
( x −a)(32x −4 3x +3)= 0
имеет два различных корня?
4.3.м Постройте график уравнения:
sin2 x +sin2 y = 2 .
4.4.м Докажите, что площадь S прямоугольного треугольника можно найти по формуле S = p (p − c) , где p — полупериметр треугольника, c —
длина гипотенузы.
72

Вариант 36
Часть вторая
Решите задания 2.1 – 2.8. Запишите ответ в бланк ответов.
2.1. Упростите выражение |
sinα+sin3α . |
|
|
|
|
|
|
|
|
|
|
cosα+cos3α |
|
|
|
|
|
|
|
|
|
2.2. Решите неравенство 4x+1 +4x ≥ 320 . |
|
|
|
|
|
|
|
|
||
|
|
|
8 |
2 |
−2 |
1 |
|
(4+ |
2) |
|
|
|
|
3 |
2 |
|
|
||||
2.3. Чему равно значение выражения |
|
|
|
|
|
|
|
|
? |
|
(3 3 − 3 2)(3 9 + 3 6 + 3 4) |
||||||||||
2.4.Решите неравенство x2 −28x +16 ≤ 0 .
x−4
2.5. Вычислите интеграл ∫2 (x2 −2x) dx .
−3
2.6.Найдите функцию, обратную к функции y = x +x 2 .
2.7.В треугольник ABC вписан ромб AKPE так, что угол A у них общий,
авершина P принадлежит стороне BC. Найдите сторону ромба, если
AB=6 см, АC=3 см.
2.8.Найдите объем правильного тетраэдра, ребро которого равно a.
Часть третья
Решение задач 3.1 – 3.3 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
3.1. Решите уравнение:
log3(4x − 3)+ log3(4x −1)= 1.
3.2.Число 60 представьте в виде суммы двух положительных чисел так, чтобы сумма их квадратов была наименьшей.
3.3.В треугольнике ABC точка O — центр вписанной окружности. Найдите радиус окружности, описанной около этого треугольника, если AO=6 см,
BO=10 см, С=60°.
73

Часть четвертая
Решение задач 4.1 – 4.4 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
4.1.м Для каждого значения параметра a решите неравенство:
(2x − a) x − 3 ≥ 0.
x − 3 ≥ 0.
4.2.м Докажите, что при всех действительных значениях x выполняется неравенство:
ex −1≥ x .
4.3.м Найдите корни уравнения:
cos3x +cos52x = 2.
4.4.м Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности катетов. Найдите острые углы треугольника.
74
Вариант 37
Часть вторая
Решите задания 2.1 – 2.8. Запишите ответ в бланк ответов.
2.1. Сколько целых чисел содержит множество решений неравенства x2(x +1)(x −4) < 0?
2.2.Решите уравнение log27 x − log7 x2 − 3= 0 .
2.3.К сплаву массой 150 кг, содержавшему 20 % меди, добавили 10 кг меди. Какое процентное содержание меди в новом сплаве?
2.4.Найдите корни уравнения:
sinx +sin2x +sin3x = 0 .
2.5. Чему равно наибольшее значение функции f (x) = 2x 3 −3x 2 −12x +1 на промежутке [0; 3]?
2.6. Найдите первообразную функции f (x) = 3x2 − 6x + 4 , график которой проходит через точку A (1;4) .
2.7.Чему равна площадь параллелограмма, диагонали которого равны 16 см и 20 см, а одна из них перпендикулярна его стороне?
2.8.Радиус основания конуса равен R, а его осевое сечение — прямоугольный треугольник. Найдите объем конуса.
Часть третья
Решение задач 3.1 – 3.3 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
3.1. Решите неравенство:
32x 2 −x +2 −52x 2 −x −1 > 52x 2 −x +1 + 32x2 −x −1.
3.2. Решите уравнение:
3x2 −9x −26 =12+3x − x2 .
3.3. В основании пирамиды лежит прямоугольный треугольник с гипотенузой c и острым углом α. Каждое боковое ребро пирамиды образует с плоскостью основания угол γ. Найдите объем пирамиды.
75

Часть четвертая
Решение задач 4.1 – 4.4 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
4.1.м При каких значениях параметра a уравнение
|
|
cos2 2x − a cos2x = 0 |
||
имеет на промежутке |
|
π;3π |
|
два корня? |
|
|
4 4 |
|
|
4.2.м Вычислите площадь треугольника, образованного осями координат и касательной к графику функции f (x) = x3 + x2 − 6x +1 в точке с абсциссой x0 = 1.
4.3.м Решите уравнение:
lg2(x +1) = lg(x +1)lg(x −1) + 2lg2(x −1) .
4.4.м В выпуклый четырехугольник ABCD можно вписать окружность. Докажите, что окружности, вписанные в треугольники ABC и ADC, касаются.
76
Вариант 38
Часть вторая
Решите задания 2.1 – 2.8. Запишите ответ в бланк ответов.
2.1. Найдите область определения функции y = 6 1− 4x .
|
|
|
|
|
|
2 |
1 |
−49 |
1 |
|
|
|
|
|||
2.2. Вычислите значение выражения 83 +164 |
2 . |
|
|
|
|
|||||||||||
2.3. Решите неравенство: |
|
x2−7x+6 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
(0,6) |
|
|
x−3 |
|
≤1. |
|
|
|
|
|
|||
2.4. Решите уравнение: |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
+ |
|
|
|
|
=1. |
|
|
|
|
|
||
|
|
5−lgx |
|
1+lgx |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
2.5. Найдите первообразную функции |
f (x) = 5x4 + 3x2 − 4 , график которой |
|||||||||||||||
проходит через точку B (–1;12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.6. Найдите точку максимума функции |
f (x) = x 4 −4x 2 . |
|
|
|||||||||||||
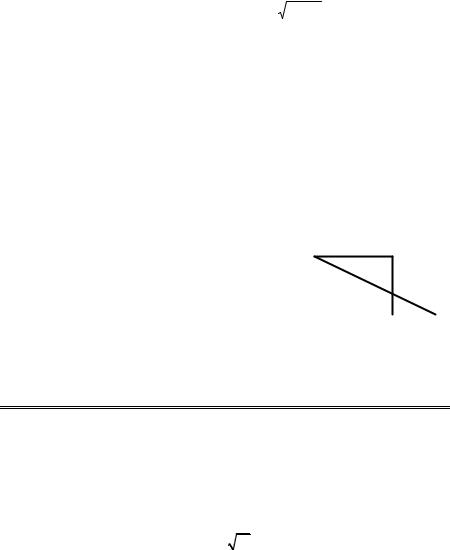
2.7. Отрезки |
AB и CD, изображенные |
на |
A |
|
|
B |
||||||||||
|
||||||||||||||||
|
|
|
|
|
||||||||||||
рисунке, |
параллельны, |
ABC = 90° , |
|
|
|
O |
||||||||||
AB = 24 см, BO =10 см, CO =5см. Найдите |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
отрезок AD. |
|
|
|
|
|
|
|
|
|
C |
|
D |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
2.8. Основание прямой призмы — прямоуголь-
ный треугольник с катетом a и противолежащим углом α. Диагональ боковой грани, содержащей гипотенузу, наклонена к плоскости основания под углом β. Найдите объем призмы.
Часть третья
Решение задач 3.1 – 3.3 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
|
|
cosα |
|
sinα |
cos6α−cos10α |
|
|
3.1. |
Упростите выражение ( |
|
− |
|
) |
sin3α |
|
cos4α |
sin4α |
||||||
3.2.Постройте график функции f (x) = 6 x6 −2x .
3.3.Основания равнобокой трапеции равны 9 см и 21 см, а высота — 8 см. Найдите радиус окружности, описанной около данной трапеции.
77
Часть четвертая
Решение задач 4.1 – 4.4 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
4.1.м Решите уравнение:
 4x − 2x − 3 =
4x − 2x − 3 =  4 2x − 7 .
4 2x − 7 .
4.2.м Найдите все значения параметра a, при которых функция f (x) = (a −12)x3 + 3(a −12)x2 + 6x + 7
возрастает на R.
4.3.м Докажите тождество:
cos(arctgx) = |
1 |
|
|
1+ x2 |
|||
|
|
4.4.м Отрезок AB является диаметром окружности, а точка C лежит вне этой окружности. Отрезки AC и BC пересекаются с окружностью в точках D и M соответственно. Найдите угол ACB, если площади треугольников DCM и ACB относятся как 1:4.
78

|
Вариант 39 |
|
|
|
|
Часть вторая |
|||
|
Решите задания 2.1 – 2.8. Запишите ответ в бланк ответов. |
|||
2.1. |
Вычислите значение выражения 81−0,5 27 |
− |
7 |
7 |
12 98 . |
||||
2.2.Решите неравенство 2 3x +3x−2 ≤ 57 .
2.3.Найдите область определения функции y = lg 33xx +−11.
2.4. |
Решите уравнение x + 4 x −6 = 0. |
2.5. |
Найдите корни уравнения cos2x = cosx . |
2.6. Найдите первообразную |
|
функции f (x) = 6x2 + e4x , график которой |
|||
проходит через точку |
|
1 |
; |
e2 |
|
A |
2 |
4 |
. |
||
|
|
|
|
||
2.7. Основание равнобедренного тупоугольного треугольника равно 24 см, а радиус окружности, описанной около него, — 13 см. Найдите боковую сторону треугольника.
2.8.Основание пирамиды — треугольник со сторонами 13 см, 14 см и 15 см. Найдите площадь сечения, которое проходит параллельно плоскости основания и делит высоту пирамиды в отношении 1:2, считая от вершины пирамиды.
Часть третья
Решение задач 3.1 – 3.3 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
3.1. Решите уравнение:
lg2 100x −5lg x = 6 .
3.2. Вычислите значение выражения:
sin20°cos70°+sin2 110°cos2 250°+sin2 290°cos2 340° .
3.3.В цилиндре параллельно его оси проведена плоскость, пересекающая нижнее основание цилиндра по хорде, которая видна из центра этого основания под углом α. Диагональ образовавшегося сечения наклонена
к плоскости основания под углом β. Найдите площадь боковой поверхности цилиндра, если площадь его основания равна S.
79
Часть четвертая
Решение задач 4.1 – 4.4 должно содержать обоснование. В нем надо записать последовательные логические действия и объяснения, сослаться на математические факты, из которых следует то или иное утверждение. Если надо, проиллюстрируйте решение схемами, графиками, таблицами.
4.1.м При каких значениях |
параметра |
a |
функция f (x) = x3 − ax2 + 3ax +1 |
|||
возрастает на всей числовой прямой? |
|
|||||
4.2.м Решите уравнение: |
x2 −2xsin πx |
|
||||
|
+1= 0 . |
|||||
|
|
|
|
|
2 |
|
4.3.м Решите систему уравнений: |
|
|
|
|||
|
9 |
x |
−4 |
5−y |
+27 = 0, |
|
|
|
3 |
||||
|
2y −3x = 4−4x + y. |
|||||
|
|
|||||
4.4.м В треугольнике ABC известно, что CAB=40°, CBA=50°. На стороне AB построен квадрат, точка M — его центр, точки C и M лежат по разные стороны от прямой AB. Докажите, что ACM = MCB.
80
