256 Глава 11 Теоретическое описание

Граничное условие нулевого потока используется для описания сверхпроводящего материала, в который не проникает магнитное поле. Векторный магнитный потенциал на поверхности таких сверхпроводников имеет постоянное (неизвестное заранее) значение (rA = const в осесимметричном случае), так что внутренность сверхпроводника исключается из рассмотрения.

Замечание. Если поверхность сверхпроводника имеет общие точки с какимлибо ребром (или узлом), где задано условие Дирихле, вся поверхность будет считаться описанной условием Дирихле, с заданным значением магнитного потенциала.

Вычисляемые физические величины

При анализе результатов расчета магнитного поля переменных токов, ELCUT позволяет оперировать со следующими локальными и интегральными физическими величинами.

Локальные величины:

Комплексная амплитуда векторного магнитного потенциала A (функция потока rA в осесимметричном случае);

Комплексная амплитуда напряжения U, приложенного к проводнику;

Комплексная амплитуда плотности полного тока jполн. = jстор. + jвихр., плотности стороннего тока jстор. и плотности вихревого тока jвихр. = i γA;

Комплексный вектор магнитной индукции B = rot A

- тензор магнитной проницаемости;

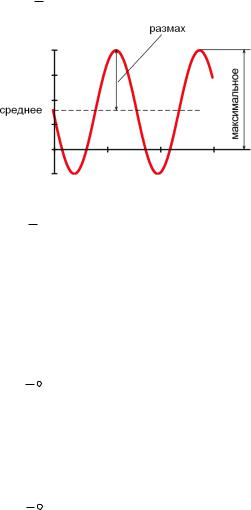
Среднее и максимальное значение удельной мощности тепловыделения

Q = γ-1 j2;

Среднее и максимальное значение плотности энергии магнитного поля w = B H / 2;

Среднее значение вектора Пойнтинга (плотность потока энергии) S = E H;

Среднее значение вектора плотности силы Лоренца F = j B;

Магнитная проницаемость (наибольшая компонента в анизотропной среде);

Электрическая проводимость γ.

Интегральные величины:

Комплексная амплитуда тока через заданную поверхность

I = jds

иеѐ сторонняя Iстор. и вихревая Iвихр. компоненты.

Среднее и максимальное значение мощности тепловыделения в объеме. А также размах колебаний.

P = 1 j2dV.

Среднее и максимальное значение энергии магнитного поля

W = 12 (H B)dV.

Среднее и максимальное значение потока электромагнитной мощности (потока вектора Пойнтинга) через заданную поверхность

S = (S n)ds.

Среднее значение пондеромоторной (полной магнитной) силы, действующей на тела, заключенные в заданном объеме

F = 12 (H(n B) + B(n H) - n(H B))ds,

где интегрирование ведется по поверхности, ограничивающей объем, а n означает вектор единичной внешней нормали к поверхности.

Среднее и максимальное значение вращающего момента пондеромоторной силы, действующей на тела, заключенные в заданном объеме

T = 12 ((r×H)(n B) + (r×B)(n H) – (r×n)(H B))ds,

258 Глава 11 Теоретическое описание

где r - радиус-вектор точки интегрирования.

Среднее значение и амплитуда колебательной части силы Лоренца, действующей на проводники с током, заключенные в заданном объеме

F= (j×B)dV.

Среднее и максимальное значение вращающего момента силы Лоренца, действующей на проводники с током, заключенные в заданном объеме

T= r× (j×B)dV,

где r - радиус-вектор точки интегрирования.

Вектор вращающего момента параллелен оси z в плоской постановке и тождественно равен нулю в осесимметричном случае. Момент вычисляется относительно начала координат. Момент относительно любой другой точки может быть получен добавлением слагаемого F r0, где F - это полное значение силы и r0 - радиус-вектор точки.

Замечание. Магнитное поле порождает силы, действующие на проводники с током и ферромагнитные тела. Сила, действующая на проводники известна под названием силы Лоренца, в то время как сила, вычисленная путем интегрирования тензора Максвелла, включает в себя обе компоненты (полная магнитная сила).

Область интегрирования определяется как разомкнутый или замкнутый контур в плоскости модели, состоящий из отрезков и дуг окружностей.

Вычисление импеданса

Импедансом в теории переменных токов называется комплексный коэффициент пропорциональности между комплексными значениями тока и напряжения, V = Z I. Его действительная часть представляет собой активное сопротивление проводника, вычисленное с учетом эффекта вытеснения тока (поверхностный эффект). Мнимая часть импеданса есть индуктивность, умноженная на угловую частоту .

Z = R + i L.

Поскольку значения напряжения и тока Вы можете легко получить в окне анализа результатов расчета, импеданс вычисляется путем деления напряжения на ток по правилам комплексной арифметики. Пусть V и I - амплитудные значения напряжения и тока, и V и I фазы этих величин. Тогда активное сопротивление вычисляется как