Основы_акустики_Гринченко_Вовк

exp(–2α1x) – exp(–α2x) в формуле (12.107), а потом уменьшается, ведь каждая экспонента стремится к нулю с увеличением значения х. Та- кое поведение второй гармоники обусловлено наличием в волновом процессе двух противодействующих факторов: нелинейности, кото- рая порождает высшие гармоники (в том числе вторую) и диссипа- ции, которая приводит к поглощению высших гармоник (тем более эффективному, чем выше номер гармоники). Можно говорить, что за счет нелинейности энергия начального гармонического сигнала боль- шой амплитуды перекачивается в область высших частот, где наблю- дается большее поглощение, чем на частоте первой гармоники (α ω2). Поэтому сигналы большой амплитуды поглощаются сильнее, чем сигналы малой амплитуды одинаковой частоты, и потому про- филь первоначально гармонической волны, который со временем де- формируется, приобретает снова синусоидальную форму.

Рассмотрим теперь влияние дисперсии при отсутствии поглоще- ния (α1 = α2 = 0). В этом случае

(12.109)

Напомним, что τ = t – x/c0, δ (ω) = –a3ω3. При малых значениях пара- метра a3 (т.е. при слабой дисперсии) первый синусоидальный мно-

житель в (12.109) как функция координаты х изменяется значительно медленнее, чем второй, что позволяет рассматривать его как огибаю- щую зависимости р(2)(х). Наличие этого множителя определяет про- странственные биения волны второй гармоники. Причина возникно- вения биений — различные фазовые скорости волн первой и второй гармоник, что является результатом дисперсии скорости звука.

Действительно, при отсутствии дисперсии δ (ω) = δ (2ω) = 0 волна вынуждающей силы F, порожденная первой гармоникой, и соответ-

ствующая ей волна p2(2) — вынужденное колебание распространяют- ся с той же скоростью, что и волна p1(2) (см. (12.102), (12.105),

(12.103)). В результате фазы вынуждающей силы F и колебания p1(2) в

каждой точке пространства совпадают. Это явление называется син- хронизмом. Вследствие синхронизма волна второй гармоники

p(2) = p1(2) + p2(2) усиливается во время распространения (см. (12.108)).

В среде с поглощением (но без дисперсии) также наблюдается син- хронизм, но появляется конкурирующий фактор — повышенное по- глощение второй гармоники по сравнению с первой, которое вначале

841

замедляет рост амплитуды второй гармоники, а потом приводит к ее уменьшению. В дисперсионной среде волновые числа вынуждающей

силы F и второй гармоники: 2k0 + 2δ(ω) = 2k0 − 2a3ω3 и

2k0 + δ(2ω) = 2k0 − 8a3ω3 различны, а, следовательно, различны и фа-

зовые скорости. Вследствие этого синхронизм нарушается. В некото- рых точках пространства вынуждающая сила поддерживает колеба- ния удвоенной частоты, а других частот ослабляет, в результате чего наблюдается картина пространственных биений (см. (12.109)) второй гармоники в отличие от монотонного роста ее амплитуды, как в

(12.108).

12.9. Солитоны

Дисперсия, как и поглощение, оказывают влияние на уро- вень высших гармоник в спектре сигнала и, таким образом, на его профиль. Физически это связано с тем, что разные спектральные компоненты распространяются с разными скоростями, что ограни- чивает накопление нелинейных эффектов, приводящих к появлению резких изменений в профиле волны. Итак, и поглощение, и дисперсия (за счет нарушения синхронизма) сдерживают действие нелинейно- сти и выступают (в данном случае) в роли конкурирующих с ней фак- торов. Если пренебречь поглощением, то оказывается возможной си- туация, когда нелинейные эффекты и эффекты, обусловленные дис- персией, уравновешивают друг друга. Этой ситуации соответствует стационарное (т.е. волна с неизменным профилем) решение уравне- ния Кортевега-де Вриза (уравнение (12.97) при а2 = 0) [28, 45]. Реше- ние имеет вид одиночного импульса и называется одиночной волной или солитоном. Последнее название происходит от английского сло- восочетания solitary wave — одиночная волна. Итак, само название волны подчеркивает локализованный характер такого решения урав- нения Кортевега-де Вриза (КдВ). Вид солитона КдВ приведен на рис. 12.7.

Рис. 12.7. Зависимость давления от τ для солитона уравнения Кортевега-де Вриза

842

Оценим его характерные параметры, считая, что нелинейный член в уравнении КдВ (см. (12.97) при а2 = 0) уравновешивается дисперси- онным:

Обозначим амплитуду солитона р0 и его характерную ширину (рис. 12.7). Тогда, как следует из соотношения (12.110), a1p02 2 a3 p0 2 , откуда получим связь между параметрами солитона:

Рис. 12.8. Эволюция начального возмущения в нелинейной среде с диспер- сией, которая завершается образованием солитонов [45, с. 26]

Как следует из соотношения, чем больше амплитуда солитона, тем он уже. Анализ точного решения уравнения КдВ подтверждает спра- ведливость соотношения (12.111). Вообще солитоны имеют очень ин- тересные свойства. Например, оказывается, что их скорость тем больше, чем больше амплитуда. Другое свойство иллюстрирует рис. 12.8 [45, с. 26], на котором представлена эволюция начального возмущения в рамках уравнения КдВ. Как следует из рисунка, про- цесс формирования резкого изменения профиля останавливается и происходит образование одного или нескольких солитонов, число ко- торых определяется начальными условиями.

843

Образование солитонов возможно в случаях, когда дисперсионные эффекты значительно преобладают над эффектами поглощения, на- пример, гравитационно-капиллярные волны на поверхности жидко- сти. Впервые одиночную волну на поверхности воды наблюдал Рассел* в 1838 г. Для звуковых волн в жидкостях и газах характерно проти- воположное соотношение, а именно: преимущество диссипации над дисперсионными эффектами. Однако в структурно-неоднородных средах, где существует акустическая дисперсия, наблюдаются эф- фекты солитонного характера [28].

12.10. Нелинейное взаимодействие акустических волн

Две волны, бесконечно малой амплитуды, проходя сквозь некоторую область среды, создают интерференционную картину, в которой взаимное усиление колебаний в одних местах и ослабление в других объясняется суперпозицией волн, приходящих в точку наблю- дения со сдвигом фаз. При конечной амплитуде хотя бы одной из двух волн, кроме интерференции, наблюдается их взаимодействие, которое выражается в появлении новых волн, что обусловлено нели- нейностью волнового процесса.

Нелинейное взаимодействие волн — одно из наиболее важных эффектов нелинейной акустики, которое уже нашло применение в технике. Чтобы понять главные особенности этого сложного явления, рассмотрим простой случай, а именно: распространение двух плоских волн p1(x,t) и p2(x,t) вдоль оси Ох. При этом одновременно рассмотрим две ситуации: когда волны распространяются в одном направлении и в противоположных направлениях.

Воспользуемся методом последовательных приближений, посколь- ку при изучении поля встречных волн нельзя ввести сопровождаю- щие координаты и применить метод медленно изменяющегося про- филя.

Итак, пусть волны первого приближения p1′ (x,t ) и p2′ (x,t ) — пло-

ские гармонические волны с частотами ω1 и ω2. Тогда в первом при- ближении звуковое давление в среде имеет вид

Верхний знак (здесь и в дальнейшем) во втором слагаемом соответст- вует распространению волн в одном направлении, нижний — рас- пространению волн навстречу друг другу; k1 = ω1/c0, k2 = ω2/c0.

* Рассел (Russell) Джон Скотт (1808—1882) — английский ученый и ин- женер-изобретатель.

844

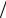
Волны второго приближения (нелинейное слагаемое р″ ) найдем с помощью уравнения (12.50). Его правую часть, выполняющую роль возбуждающей силы, которая действует вдоль оси Ох, определим че-

Волновое уравнение (12.50) есть линейное уравнение, и поэтому согласно принципу суперпозиции каждому слагаемому в (12.113) со- ответствует свое решение. Так, Q11 отвечает за появление второй гармоники в волне p1(x,t), а Q22 обусловливает появление второй гар- моники в волне p2(x,t). Это, как уже мы понимаем, приведет к изме- нению профиля взаимодействующих волн. Слагаемое Q12 собственно и определяет взаимодействие волн.

(12.115)

то, согласно (12.115), слагаемое Q12 делится на две компоненты, кото- рые имеют смысл вынуждающих сил суммарной частоты (ω1 + ω2) и разностной частоты (ω1 – ω2). Под их влиянием в среде возникают волны суммарной и разностной частот, которые являются следствием нелинейного взаимодействия волн с частотами ω1 и ω2.

Рассмотрим компоненту разностной частоты (ω1 – ω2). Это связано с тем, что во многих случаях данная компонента представляет наи- больший интерес, ведь в реальной среде за счет поглощения все вы- сокочастотные составляющие быстро затухают.

После дифференцирования в (12.114) находим

(12.116)

Под действием вынуждающей силы (12.116) в среде возникает волна разностной частоты (ω1 – ω2):

845

Очевидно, характер изменения амплитуды B(x) этой волны зави-

сит от направления распространения волн p1(x,t) и p2(x,t). Действи- тельно, если волны распространяются в одном направлении, то фазы

вынуждающей силы Q12− и волны p− совпадают в каждой точке сре-

ды, ведь (k1 – k2)x = (ω1 – ω2)x/c0, и наблюдается синхронизм. В этом случае В(х) будет нарастать линейно с координатой х, ведь во время распространения именно эта фазовая синхронность обеспечивает по-

стоянное поступление энергии к волне p− .

Если волны распространяются навстречу друг другу, то явление синхронизма отсутствует, ведь (k1 +k2 )x ≠ (ω1 − ω2 )x c0 . В этом случае можно говорить о некоторых пространственных биениях и, разумеется, возбуждение волны p− будет малоэффективным.

Из этих качественных рассуждений мы делаем важный вывод: эффект возбуждения волны p− с разностной частотой (ω1 – ω2) в зна-

чительной мере зависит от направления движения волн с частотами ω1 и ω2, и, как оказывается, является наиболее эффективным, когда волны p1(x,t) и p2(x,t) распространяются в одном направлении.

Рассмотренная ситуация взаимодействия плоских волн в идеаль- ной среде представляет собой достаточно упрощенную модель взаи- модействия. Отметим основные моменты реальной среды, которые оказывают влияние на эффект взаимодействия волн. Во-первых, это наличие поглощения в реальной среде. Во-вторых, это дисперсия ско- рости звука, хотя для таких сред, как вода и воздух, этот фактор не имеет большого значения, ведь дисперсия практически отсутствует. И, в-третьих, то, что сами волны не являются плоскими, а представ- ляют собой пучки, которые за счет дифракции распространяются в зону геометрической тени.

Таким образом, наличие в среде дисперсии приводит к несин- хронному взаимодействию волн, распространяющихся в одном на- правлении. Наличие поглощения и дифракционного расширения пучка ограничивает зону эффективного взаимодействия волн, рас- пространяющихся в одном направлении.

12.11. Параметрические излучатели и приемники звука

До 1960 года в ряде исследований было показано, что в

846

ультразвуковом диапазоне частот, даже при небольших интенсивно- стях звука, гармоники и волны комбинационных (ω1 + ω2, ω1 – ω2) час- тот в слабовязких жидкостях (таких, например, как вода) благодаря нелинейным свойствам генерируются достаточно сильно. Проанали- зировав это явление, американский акустик Вестервелт (Westervelt, 1963 г.) и, независимо от него, Зверев* и Калачев пришли к мысли о возможности создания параметрических излучающих и приемных ан- тенн. В таких антеннах излучающими или приемными элементам яв- ляется сам объем нелинейной среды, в котором происходит взаимо- действие волн.

Введенный Вестервелтом термин “параметрический” не соответст- вует принятому в теории колебаний понятию параметрического возбу- ждения. Точнее было бы говорить о нелинейной антенне. Однако этот срок настолько крепко вошел в научный язык специалистов, что по- пытки изменить его не имеют смысла [37, с. 129].

Рис. 12.9. Схема параметрического излучателя звука: 1 — излучатель звука, L — длина области взаимодействия

На рис. 12.9 представлена схема излучающей параметрической ан- тенны. Две интенсивные волны с близкими частотами ω1 и ω2, распро- страняющиеся в одном направлении, взаимодействуют между собой. При этом вместе с другими частотами появляется разностная часто- та Ω = ω1 − ω2 << ω1,ω2 . Так, для воды значения ω1 и ω2 удобно выби-

рать в диапазоне приблизительно до нескольких сотен килогерц. Ес-

ли, например, ω1/2π = 100 кГц, ω2/2π = 99 кГц, Ω/2π = 1000 Гц, то волна с частотой Ω поглощается значительно слабее, чем волны с час- тотами ω1 и ω2. Поэтому эта волна сможет пройти значительно боль- шее расстояние, чем волны ω1 и ω2. Понятно, что эффективность та- кой излучающей антенны невелика, однако, несмотря на это, такая антенна обладает очень ценными свойствами.

Прежде всего, — это острая характеристика направленности для волны с частотой Ω. При этом сам излучатель, создающий в среде

* Зверев Виталий Анатольевич (р. 1924 г.) — российский радиофизик и аку- стик, чл.-кор. РАН.

847

волны с частотами ω1 и ω2, может иметь малые размеры по сравне- нию с длиной волны на частоте Ω. Чтобы оценить направленность параметрической антенны, сравним ее с направленностью обычной антенны, которая также излучает волну с частотой Ω.

Рис. 12.10. Пример антенны в виде набора ненаправленных излучателей

В параметрической антенне полезный сигнал возникает за счет действия на среду вынуждающей силы Q12− (x,t ) (формула (12.116)),

которая имеет характер бегущей волны. Расположим на отрезке L (рис. 12.10), длина которого равна длине области эффективного взаимодействия волн с частотами ω1 и ω2, обычные ненаправленные излучатели (например, пьезокерамические) и настроим их фазы та- ким образом, чтобы максимум излучения полученной антенны сов- падал с направлением излучения параметрической антенны, т.е. вдоль оси Ох. Для этого, как известно, необходимо ввести фазовые сдвиги для компенсации разности хода от отдельных излучателей до точки приема на оси Ох. При этом возбуждение элемента антенны с координатой х на частоте Ω будет определяться соотношением cos(Ω(t ––x/c0)), что совпадает с точностью до постоянного множите- ля с формулой (12.116), в которой взят верхний знак. Отсюда следу- ет, что направленность параметрической антенны определяется размером зоны взаимодействия L и близка к направленности обыч- ной фазированной антенны длиной L. Поскольку в реальной ситуа- ции размер L достаточно велик, то направленность параметрической антенны может быть острой (в гидроакустических параметрических антеннах величина L достигает сотен метров).

Параметрическая антенна привлекательна не только тем, что она бестелесная и может иметь гигантские размеры. У нее есть очень важное принципиальное преимущество перед антенной, которая представляет собой решетку из обычных ненаправленных элементов. Дело в том, что фазы отдельных элементов необходимо настраивать между собой с высокой точностью. Это сложная техническая задача. Необходимо обеспечить не только идентичность как фазовых, так и амплитудных характеристик многих элементов антенны, но и их точ- ное расположение. Точность выполнения этих операций остается ко- нечной при любых усилиях. Вследствие этого, такая антенна имеет боковое поле, которое, к сожалению, невозможно заранее точно рас- считать. Это поле существенно портит характеристику антенной ре- шетки. Вообще, теоретически, антенна в виде фазированной решет- ки всегда имеет боковое поле.

848

Рис. 12.11. Характеристики направленности излучения параметрической антенны [23, с. 103]:

на частотах f1 = 418 кГц (а) и f2 = 482 кГц (б), на разностной частоте Ω/(2π) = 64 кГц (в)

Параметрическая антенна имеет исключительное свойство — у нее нет боковых лепестков, наличие которых является типичным для обычных антенн. В качестве примера, на рис. 12.11 приведены ха- рактеристики направленности плоского излучателя диаметром 7,5 см на частотах f1 = 418 кГц (рис. 12.11, а), f2 = 482 кГц (рис. 12.11, б) и

направленность волн разностной частоты Ω/2π = 64 кГц (рис. 12.11, в) [23, с.103]. Из рисунка следует, что на частоте Ω дифракционные лепестки отсутствуют. Другой важной особенностью является широ- кополостность параметрической антенны. Действительно, изменяя частоты f1 и f2 электрических сигналов, можно получить плавное из- менение частоты Ω в широких пределах.

Указанные свойства параметрических антенн очень важны, нали- чие этих свойств обусловливает интерес к таким антеннам. Особенно это касается гидроакустики. Здесь параметрические антенны нахо- дят разнообразные применения. Узкая характеристика направленно- сти с подавленными боковыми лепестками дает возможность переда- вать сигналы на морском мелководье и позволяет не учитывать по- сторонние сигналы, появляющиеся вследствие отражения от поверх- ности моря и его дна. Широкополостность параметрической антенны дает возможность перестраивать частоту Ω и добиваться максимума рассеянного объектом сигнала на его резонансной частоте. Так осу- ществляется поиск и классификация затонувших объектов, даже если они засыпаны слоем ила, ведь низкочастотные волны вследствие ма- лого поглощения проникают в слои ила.

Нелинейное взаимодействие волн в жидкостях или газах может быть использовано и для приема слабых сигналов. Принцип действия приемной параметрической антенны представлен на рис. 12.12. Из-

849

лучатель 1 частоты ω (накачка) создает достаточно узкий пучок ин- тенсивных звуковых волн. Величина L определяет длину приемного луча. Слабый сигнал частоты Ω << ω падает под некоторым углом θ к оси пучка. В области взаимодействия L волна сигнала распространя- ется в среде, параметры которой изменяются мощной волной накач- ки, вследствие чего регистрирующий преобразователь 2 принимает волну накачки, модулированную волной сигнала. Дальше схема обра- ботки 3 выделяет параметры сигнала. Фактически прием сигнала происходит на длине базы L, а, следовательно, приемная антенна яв- ляется “бестелесной”.

Рис. 12.12. Схема параметрического приемника звука:

1 — излучатель волны накачки; 2 — электроакустический преобразователь; 3 — схема обработки; L — область взаимодействия (длина приемного луча)

По результатам параграфа 12.10 можно сделать следующие выво- ды. Эффективность возбуждения волн с частотами ω – Ω и ω + Ω бу- дет максимальной в случае распространения волн накачки и сигнала в одном направлении, т.е. при угле падения волны сигнала θ = 0°. Итак, максимум характеристики направленности приемной парамет- рической антенны расположен в направлении, противоположном на- правлению распространения волны накачки.

Перспективным является применение параметрических приемни- ков в электроакустике, где средой является воздух: речь идет о пара- метрическом микрофоне. В конце данного раздела приведем отрывок из статьи Зверева [*, с. 691—692], в котором автор делится впечатле- ниями об испытаниях лабораторного макета параметрического мик- рофона.

“С помощью лабораторного макета параметрического микрофона, приемный луч которого имел длину 1 м, мы недавно провели такой эксперимент. В небольшой комнате одновременно разговаривали (ка- ждый о своем) все, кто принимал участие в создании макета микро- фона (5 человек). Из них только один находился там, где звук его го- лоса распространялся вдоль ультразвукового луча. Итак, произошло

* Зверев В.А. Как зарождалась идея параметрической акустической ан- тенны // Акустический журнал. — 1999. — 45, № 5. — С. 685—692.

850