Основы_акустики_Гринченко_Вовк

более пригодна для удовлетворения граничных условий на жестких границах. В случае же акустически мягких сторон (нулевым для них есть давление) преимущество нужно отдать другой системе.

Возможность вариации формы решения при сохранении общего характера, безусловно, определяет гибкость метода частичных облас- тей. В конце этого параграфа еще раз обратим внимание на важное, по сути, отличие задач для составного волновода (рис. 10.1), с одной стороны, и для треугольной области (рис. 10.3), с другой. Если в пер- вой задаче граничная поверхность области существования звукового поля описывалась частями координатных поверхностей одной систе- мы координат, то в задаче для треугольной области это уже не так.

Таким образом, сама возможность работы одновременно в разных системах координат существенно расширяет круг задач акустики, которые допускают построение аналитического решения.

10.5. Дополнение граничных условий

В продолжение предыдущего параграфа опишем способ, который также существенно расширяет возможности метода частич- ных областей при исследовании звуковых полей в сложных (некано- нических) областях. Дело в том, что возникают ситуации, когда при использовании даже явно полных решений граничной задачи могут возникнуть трудности при преобразовании функциональных уравне- ний в алгебраические. Вот здесь возникает специфическая задача

продолжения граничных условий с физически заданной границы на некоторый несуществующий участок. Прежде, чем описать способ преодоления таких трудностей, приведем некоторые математические сведения.

Согласно теореме Дирихле [8], если функция Ф (х), заданная на отрезке [–a,a] и являющаяся на нем кусочно-непрерывной, кусочно- монотонной и ограниченной, то ее тригонометрический ряд Фурье сходится во всех точках отрезка [–a,a]. При этом, если S (x) — сумма тригонометрического ряда Фурье функции Ф(х), то во всех точках не- прерывности этой функции S(x) = Ф(х), во всех точках разрыва перво-

отрезка [–a,a] играют особую роль, подобную роли точек разрыва.

Дирихле (Dirichlet) Петер Густав Лежён (1805—1859) — немецкий мате- матик.

622

Рис. 10.5. Пример излучающей системы из двух цилиндров:

а — цилиндры пересекаются; б — цилиндры не касаются друг друга

Рассмотрим идею дополнения граничных условий на примере за- дачи об излучении звука сложной (неканонической) поверхностью. Речь идет о плоской задаче, в которой имеем два пересекающихся цилиндра с параллельными осями. Для простоты возьмем два цилин- дра с одинаковым радиусом а (рис. 10.5, а).

Сначала рассмотрим ситуацию, когда цилиндры не касаются друг друга (рис. 10.5, б). Такая задача хорошо изучена [60, с. 139—142]. Введем две полярные системы координат r1O1θ1 и r2O2θ2 с центрами

O1 и O2 на осях цилиндров.

В соответствии с п. 7.12.1, поле давления отдельно взятого цилин- дра, например первого (слева), описывается соотношением (7.128), представляющим собой суперпозицию цилиндрических волн:

(считаем, что функция четная относительно угловой координаты, по- этому можно использовать только функции косинуса). Здесь коэффи-

циенты An(1) определяются из граничного условия на поверхности пер-

вого цилиндра. Это условие состоит в задании радиальной скорости на поверхности цилиндра, т.е.

Подставляя (10.52а) в (10.52б) и, используя свойство ортогональности системы функций cos (nθ1 ), n =1,2,... на отрезке [0,2π], определяем

624

коэффициенты An(1). Аналогично, если в пространстве имеем только второй цилиндр (справа), то его поле давления имеет вид

Теперь вернемся к задаче излучения двух цилиндров, которые не касаются друг друга (рис. 10.5, б). Здесь по сравнению с одним ци- линдром ситуация усложняется. Дело в том, что звуковое поле в точке наблюдения M состоит из звуковых полей, которые излучает каждый цилиндр, причем излучение каждого из цилиндров должно быть оп- ределено с учетом многократного рассеяния звука на цилиндрах. По- этому поле давления пары цилиндров определим как сумму давлений p1 и p2, т.е.

где коэффициенты An(1) и An(2) нужно выбирать так, чтобы одновре-

менно удовлетворить граничные условия на поверхностях обоих ци- линдров:

на поверхности первого цилиндра

Следует отметить, что в (10.54) волны записаны в разных системах ко- ординат, связанных с центрами каждого из цилиндров. Поэтому, чтобы можно было выполнить дифференцирование и удовлетворить гранич- ное условие (10.55) на поверхности первого цилиндра, необходимо за- писать волны, которые излучаются вторым цилиндром в системе коор- динат r1O1θ1 с центром в точке O1. Аналогичное замечание имеем отно- сительно граничного условия (10.56) на поверхности второго цилиндра.

625

Перенос начала отсчета в точку O1 или O2 можно выполнить, ис-

пользуя теорему сложения для цилиндрических функций [49, 60, ].

Согласно этой теореме имеем [49, с. 184]:

где (r1,θ1) и (r2,θ2) — координаты точки наблюдения M в соответст- вующих системах координат (рис. 10.5).

Используя теорему сложения для цилиндрических функций, под- ставляем (10.54) в условия (10.55), (10.56) и получаем пару функцио- нальных уравнений. Алгебраизация первого из них осуществляется

вследствие ортогональности системы функций cos (nθ1 ), n = 0,1,2,..., на отрезке [0,2π], а второго — вследствие ортогональности системы функций cos (nθ2 ), n = 0,1,2,..., на отрезке [0,2π]. Таким образом, по-

лучим бесконечную систему линейных алгебраических уравнений второго рода:

решение можно получить благодаря редукции бесконечной системы. Теперь рассмотрим ситуацию, когда цилиндры пересекаются (рис.

10.5, а). Здесь граничные условия на штриховых участках окружно- стей не определены, поскольку эти участки вообще не являются физи- ческими границами области. Итак, функции V1(θ1) и V2(θ2) не опреде- лены на полных окружностях, поэтому воспользоваться ортогонально- стью систем функций cos(nθ1) и cos(nθ2) нет возможности. Алгебраи- зация функциональных уравнений при таких условиях приведет к появлению системы алгебраических уравнений первого рода вида (10.14), что, как уже отмечалось выше, является нежелательной си- туацией.

Используя идею продолжения граничных условий, записываем граничное условие для левого цилиндра (рис. 10.5, а) таким образом:

Ерофеенко В.Т. Теоремы сложения. — Минск: Наука и техника, 1989. — 225 с.

626

где функция f1(θ1) определяет дополнение граничных условий для ре- шения p1 на нефизическом участке поверхности левого цилиндра. Аналогичное соотношение запишем для правого цилиндра:

где функция f2(θ2) определяет дополнение граничных условий для ре- шения p2 на нефизическом участке правого цилиндра.

Теперь мы получили возможность воспользоваться ортогонально- стью систем функций cos(nθ1) и cos(nθ2) на отрезке [0,2π] и преобразо-

вать функциональную систему уравнений (10.59), (10.60) в бесконеч- ную систему алгебраических уравнений второго рода вида (10.58).

Следует отметить, что как показано в работе [60, с. 142-144] при- менение теоремы сложения для цилиндрических функций в данной задаче возможно в том случае, когда цилиндры не касаются друг дру- га. В противном случае соответствующие ряды вида (10.16) расходят- ся. Поэтому в задаче с пересекающимися цилиндрами следует, ис- пользуя формулы связи между полярными системами координат r1O1θ1 и r2O2θ2 , провести численное интегрирование при определении

коэффициентов матрицы.

Рис. 10.6. Нормированные кривые колебательной скорости и давления на поверхности излучателя: а − f1 (θ1 ) = f2 (θ2 ) = 0 ; б − f1 (θ1 ) = f2 (θ2 ) =V0 .

627

На рис. 10.6 приведены некоторые расчеты для излучающей сис- темы (рис. 10.5, а) при волновом размере радиуса цилиндров aλ =1,2 и волновом расстоянии между осями цилиндров dλ =1,8 .

При таких размерах угол θ0 ≈ 41,4 . На излучающих поверхностях за- дано равномерное распределение колебательной скорости (V1 (θ1 ) =V2 (θ2 ) =V0 ). В бесконечных рядах удерживалось по 20 коэф-

фициентов An(1) и An(2). На рис. 10.6 представлены расчеты колеба-

тельной скорости и давления на поверхности излучателя, нормирован- ные к V0 и ρcV0, соответственно. При этом, рис. 10.6, а соответствует ситуации, когда на штриховых участках цилиндрических поверхно- стей задается нулевая скорость, а рис. 10.6, б — та же скорость, что и на активной части границы, т.е. V0.

Как видим, непрерывное продолжение граничных условий на всю поверхность цилиндров (рис. 10.6, б) существенно улучшает сходи- мость метода редукции при нахождении решения бесконечных сис- тем уравнений и вычислении характеристик поля. В этом случае при

указанном количестве удержанных коэффициентов An(1) и An(2) полу-

чено практически точное решение. При задании на продолжении границ нулевых значений колебательной скорости (рис. 10.6, а) схо- димость, как это всегда бывает при суммировании рядов Фурье, ухуд- шается. Существенное отличие между кривыми на рис. 10.6, а, б на- блюдается лишь в зоне вблизи точек пересечения цилиндров (здесь

θ0 ≈ ≈ 41,4 ). Однако численный эксперимент показывает, что при

увеличении количества учтенных коэффициентов An(1) и An(2) оценки

характеристик ближнего и дальнего полей приближаются друг к дру- гу.

Здесь следует сделать важное замечание. Дело в том, что продол- жение граничных условий на нефизическую поверхность левого ци- линдра проведено только для решения p1, а дополнение граничных условий на нефизическую поверхность правого цилиндра — только для решения p2. Понятно, что указать, каким должен быть выбор функций f1(θ1) и f2(θ2), которые определяют продолжение граничных условий на нефизические участки границы, невозможно. И все же, основываясь на рассуждениях, которые характерны для конкретной за- дачи, нужно стремиться к уменьшению разрыва функции в точке, где стыкуются граничные условия на физическом и нефизическом уча- стках поверхности тела. Отметим еще раз, что результат на рис. 10.6, б оказался очень удачным.

Подводя итоги, можно сказать, что большое количество практиче- ских вычислений и строгий анализ некоторых простых задач [14] приводят к необычному, на первый взгляд, выводу, а именно, окон-

628

чательные количественные оценки характеристик поля не зависят от выбора функций, которые дополняют граничные условия на не- физическом участке границ (в данной задаче это f1 (θ1) и f2 (θ2)). Та-

ким образом, описанный способ улучшения свойств бесконечных систем, полученных во время решения задачи, является действитель- но конструктивным и, следовательно, расширяет возможности мето- да частичных областей.

Рассмотренный выше материал дает общую характеристику мето- да частичных областей и раскрывает его возможности. Следующие параграфы посвящены построению на базе метода частичных облас- тей решению интересных и в то же время важных для практики своими результатами граничных задач акустики.

10.6. Распространение звука в нерегулярных волноводах

Слово регулярный происходит от латинского слова regularis, т.е. равномерный, правильной формы. Таким волноводом является плоский волновод, который мы исследовали в параграфе 5.11, или волновод в виде трубы постоянного сечения. Теперь речь будет идти о волноводах, в которых их регулярность нарушается, причем изменение соответствующих характеристик волновода проис- ходит не постепенно, а, наоборот, резко (например, составной волновод, см. рис. 10.1). Неоднородные волноводы такого типа находят широкое применение в акустических и радиоэлектронных устройствах. По- нятно, что исследование нерегулярных волноводов значительно слож- нее, чем регулярных.

10.6.1. Распространение звука в волноводе с изгибом

На рис. 10.7, а-в изображен плоскопараллельный волновод с изгибом, заполненный идеальной средой плотностью ρ, со скоро- стью звука c. Характерные размеры волновода до и после изгиба рав- ны h1 и h2, соответственно. Величина изгиба характеризуется углом θ, он может быть острым, прямым и тупым. Поверхности волновода считаем акустически жесткими, тогда производная от давления по нормали на этих поверхностях равна нулю:

Разделим всю область существования звукового поля на частич- ные области. Для этого, из угловой точки, образованной верхними границами волновода, опустим перпендикуляры на нижние границы. Итак, получим три области. Как показано на рис. 10.7, а, введем две

629

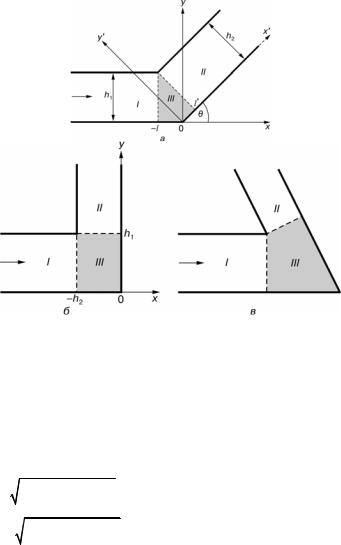
декартовые системы координат xOy и x′Oy′ с общим центром в точке O. Пусть слева на изгиб падает одна из мод области I (см. параграф 5.11):

exp(−iωt ) опускаем). Вследствие ее взаимодействия с изгибом образу-

ется отраженная волна и волна, прошедшая в область II. Отраженную волну представим в виде суперпозиции мод области I. Тогда в систе- ме координат xOy, давление звукового поля в области I запишем в виде

Рис. 10.7. Пример плоского волновода с изгибом: а — угол изгиба острый; б — прямой; в — тупой