Основы_акустики_Гринченко_Вовк

На рис. 10.17 представлены частотные зависимости коэффициен- тов W (1) и Wу(1) в случае падения на ответвление первой моды (q =1) ;

h1 = h2 = h.. Следует отметить, что при h < 0,9λ большая часть энергии проходит в ответвление (Wу(1) > W (1)). С увеличением частоты наблю- дается увеличение коэффициента W (1) и уменьшение Wy(1) с характер-

ными подъемами и спадами в зоне “критических” частот, которые со- ответствуют зарождению очередной моды волновода. Как и в случае на рис. 10.16, с увеличением волнового размера волновода на определен- ном частотном интервале доминирует очередная мода области III. Модо- вая структура области II определяется первой нормальной волной.

Рис. 10.17. Частотные зависимости коэффициентов W (1) (кривая 1) и Wу(1) (кривая 2) при h1 = h2 = h

10.6.3. Прохождение звука через область сопряжения плоского и клинообразного волноводов

Задача прохождения волны через область стыка плоского и клинообразного волноводов (рис. 10.18) неоднократно исследовалась специалистами в области акустики и электродинамики. При этом большая часть работ посвящена частному случаю: излучению из вол- новода с плоским фланцем (рис. 10.18, б). Построим решение сфор- мулированной задачи при условии произвольного угла раскрыва кли- нообразного волновода.

Итак, имеем плоский волновод с характерным размером 2h, кото- рый граничит с клинообразным волноводом с углом раскрыва 2θ0 (рис. 10.18, а-в): угол раскрыва может быть острым, прямым или ту-

641

пым. Волноводная структура заполнена идеальной средой плотностью ρ, со скоростью звука c. Поверхности волновода являются акустиче- ски жесткими.

Согласно рис. 10.18, а вводим декартову xOy и полярную rOθ сис- темы координат с общим центром O. Вся область существования зву- кового поля естественно делится на частичные области: I — плоский полубесконечный волновод x ≤ x0, y ≤ h; III — клинообразный волно-

вод r ≥ r0, θ ≤ θ0 ; II — переходная область — это часть круга радиуса r0.

Рис. 10.18. Пример волноводной структуры: а — угол раскрыва острый; б — прямой; в — тупой

Пусть слева сторону в области I на зону сопряжения плоского и клинообразного волноводов падает одна из мод плоского волновода. В результате ее взаимодействия с зоной сопряжения образуется отра- женная и прошедшая волны в область III. Согласно методу частичных областей следует записать выражения для звуковых полей в областях I-III. Каждое из этих выражений должно иметь общий характер, кото- рый позволяет удовлетворить любые граничные условия на границах

642

раздела частичных областей. Для области I такое выражение содер- жит в себе падающую волну и полную совокупность однородных и неоднородных отраженных волн:

где q — номер падающей моды, а величины αn определяется согласно условию ∂pI ∂y = 0 при y = ±h на жестких поверхностях плоского

волновода, а именно,

Совокупность произвольных коэффициентов An позволит выполнить условия сопряжения полей на границе раздела областей I и II.

Определим вид звукового поля в клинообразном волноводе (об- ласть III). Естественно, подобно плоскому волноводу, следует записать совокупность нормальных волн клинообразного волновода. Хотя речь о модах клинообразного волновода еще не шла, однако представить их вид несложно. Вернемся к п. 7.12.1, в котором была рассмотрена задача излучения звука цилиндром. Если имеем плоскую задачу, т.е. колебательная скорость поверхности цилиндра зависит только от уг- ла, то поле определяется суперпозицией цилиндрических волн (см. (7.128)):

∞

p (r,θ) = ∑ Bn Hn(1) (kr )cos (nθ). (10.81)

n =0

Вид угловых функций cos(nθ) физически понятен, поскольку, обойдя

цилиндр по окружности, попадаем в одну и ту же точку звукового по- ля, при этом угол изменяется на величину 2π, а давление в формуле (10.81) остается неизменным. Теперь представьте себе, что к поверх- ности цилиндра приложены две плоскости, которые образуют клино- образный волновод с углом раскрыва 2θ0 (на рис. 10.18, а частью по- верхности воображаемого цилиндра является криволинейная граница области II). Очевидно, что в такой ситуации формула (10.81) не спра- ведлива. Ее следует скорректировать в соответствии с граничными условиям на жестких границах клинообразного волновода, принимая во внимание, что производная по нормали на поверхностях клинооб- разного волновода представляет собой производную по углу θ при постоянном r (рис. 10.18). Итак, поле в области III запишем в виде

643

где, согласно граничному условию ∂pIII ∂θ = 0 при θ = ±θ0 на поверх- ностях клинообразного волновода, находим, что βn = nπθ0 . Радиаль-

ные функции Hβ(1n) (kr) (функции Ханкеля первого рода) выбраны в со-

ответствии с условиями излучения. Последовательность произвольных коэффициентов Bn определяется условиями сопряжения на границе раздела областей II и III.

Теперь построим общее решение для области II. Из полученного решения будет следовать, что волновое поле отличается для углов раскрыва θ0 ≤ 90° (рис. 10.18, а, б) и углов θ0 > 90° (рис. 10.18, в). По-

Отметим, что знак показателя экспонент в первой сумме выбран та- ким, чтобы амплитуда неоднородных волн уменьшалась внутри об- ласти II. Во второй сумме в качестве радиальных функций взяты функции Бесселя первого рода Jβn (kr). Среди частных решений урав-

нения Бесселя (7.115) целесообразно использовать именно эти функции, ведь, область II имеет конечные размеры, а функции Jβn (kr) определяют стоячую волну и не имеют особенностей при kr →

0 (см. асимптотику (8.40)).

Условия сопряжения на границах раздела областей I, II, III (рис. 10.18, а, б) имеют вид

Подставляя решения (10.79), (10.82), (10.83) в условия (10.84) и учи-

тывая формулы, которые определяют связь между декартовой и по- лярной системами координат, приходим к системе функциональных уравнений. Использование свойства ортогональности системы функ-

ций cos (αny), n = 0,1,2,... для первых двух уравнений системы (10.84) и системы функций cos (βn θ), n = 0,1,2,... для третьего и четвертого

уравнений, дает возможность провести алгебраизацию функциональ- ной системы. Как следствие, получаем бесконечную систему линей- ных алгебраических уравнений второго рода относительно искомых коэффициентов An, Bn, Cn, Dn (вид системы достаточно громоздкий, поэтому ее не приводим, но, при желании, читатель сможет получить эту систему самостоятельно).

Теперь рассмотрим случай, когда θ0 > 90° (рис. 10.18, в). Здесь центр полярной системы координат (точка O) смещается вглубь об- ласти II. Поэтому, угловые функции в выражении pII(2) (см. (10.83)) должны быть периодическими с периодом 2π, что соответствует пол- ному обходу вокруг точки O. Понятно, что такому условию не удовле-

творяет система функций cos (βn θ), n = 0,1,2,... в решении pII(2). По- этому ее следует заменить системой функций cos (nθ), n = 0,1,2,...,

которая имеет такую периодичность и является полной и ортогональ- ной на отрезке θ = [0;2π]. Таким образом, формулу (10.83) перепишем

в виде:

бой только часть окружности радиуса r0. Эту сложность можно пре- одолеть, если для решения pII(2) дополнить границу области II до пол- ной окружности радиуса r0. На рис. 10.18, в это штриховая линия в области I r = r0 , θ0 ≤|θ|≤ π. Таким образом, мы получаем возможность,

пиальным моментом является то, что при формировании граничных условий на дополнительном участке границы (r = r0 , θ0 ≤|θ|≤ π) может

быть задано произвольное значение давления или колебательной ско- рости. Пусть это значение определяется некоторой функцией f (r0,θ).

Неизвестно, какой должна быть функция f (r0,θ), чтобы непрерывно

645

продолжить решение pII(2) на дугу r = r0, θ0 ≤|θ|≤ π. Все же, в каждой

конкретной задаче следует стремиться к уменьшению скачка функ- ции на данном участке границы.

Алгебраизация первых двух уравнений в системе (10.86) осуществля- ется с помощью системы функций cos (αny), n = 0,1,2,..., ортогональ-

которое содержит в себе два уравнения, объединенных фигурной скобкой, — с помощью функций cos (nθ), n = 0,1,2,... , ортогональных на отрезке θ = [0,2π].

Построенное решение дает возможность провести анализ звуково- го поля в волноводной структуре, представленной на рис. 10.18. Ин- тересно определить угловое распределение квадрата амплитуды дав- ления в клинообразном волноводе:

где q — номер падающей моды в области I; θ — угол, который опре- деляет направление максимальной амплитуды давления на расстоя- нии r. Известно (см. параграф 7.6), что соотношение (10.87) не будет зависеть от расстояния r, если рассматривать звуковое поле в даль- ней зоне от границы раздела плоскопараллельного и клинообразного волноводов (kr >> 1). Учитывая это, подставляем в (10.87) выражение

(10.82) с учетом асимптотики функции Ханкеля Hβ(1)n (kr ) при kr → ∞ :

646

В результате имеем выражение для характеристики направленности по интенсивности, которое определяет угловое распределение энергии в дальнем поле клинообразного волновода:

Конечно, следует рассмотреть энергетические характеристики прохождения звуковой волны через границу раздела плоского и кли- нообразного волноводов. Как и в задаче о волноводе с изгибом (см. (10.71)), коэффициент прохождения W (q) определим как отношение среднего потока мощности волны в области III к среднему потоку мощности q-й моды, падающей на границу раздела волноводов в об- ласти I. После ряда преобразований, подобных тем, которые были проделаны в формуле (10.72), получим

где ε0 =1, εn =1/2, n > 0. Согласно выражению (10.90), коэффициент

прохождения представлен в виде суммы энергетических коэффици- ентов возбуждения мод области III. Аналогично коэффициент отра- жения имеет вид

Здесь число N определяет количество однородных мод области I. Из закона сохранения энергии следует необходимость выполнения усло-

вия W (q) + V (q) = 1.

Полученные бесконечные системы алгебраических уравнений ре- шались с помощью редукции. Еще раз подчеркнем, если не интересо- ваться тонкой структурой поля скорости вблизи ребер, то применение простой редукции к бесконечным линейным алгебраическим уравне- ниям второго рода целиком оправдано и эффективно. Количество уч- тенных неизвестных коэффициентов, которое определяет порядок системы, зависит от соотношения длины звуковой волны и характер- ных размеров волновода. Уменьшение длины волны, естественно, требует увеличения количества членов ряда, определяющего звуко-

647

вые поля в частичных областях. Критерием оценки качества реше- ния является точность выполнения условий сопряжения на границах частичных областей и выполнение соотношения для закона сохра-

ность выполнения закона сохранения энергии, не хуже, чем 0,1 %) обеспечивается при удержании 10...15 членов ряда для давления в частичных областях. Объем вычислений при этом оказывается не- большим, и можно получить оценку для многих характеристик звуко- вого поля в широком диапазоне частот.

Рис. 10.19. Частотные зависимости коэффициента W (0) при различных уг- лах раскрыва θ0:

1 — θ0 = 5°; 2 — θ0 = 25°; 3 — θ0 = 45°; 4 — θ0 = = 90°; 5 — θ0 = 110°; 6 — θ0 = 140°; 7 — θ0 = 180°

На рис. 10.19 приведены частотные зависимости коэффициента прохождения W(0) нулевой моды (q = 0) области I при разных углах раскрыва θ0. Здесь кривая 7 определяет излучение звука из открыто- го конца плоского полубесконечного волновода с жесткими граница-

λ — длина звуковой волны. Все кривые на рис. 10.19 указывают на увеличении энергии, которая проходит в клинообразный волновод при уменьшении угла раскрыва θ0. При малых волновых размерах 2h/λ прохождение энергии из плоскопараллельного волновода в кли-

Вайнштейн Л.А. Теория дифракции и метод факторизации. — М.: Сов.

радио, 1966. — 431 с.

648

нообразный волновод очень мало. Как видим, даже пятиградусное расширение волновода оказывается эффективным отражателем энергии. Интересно, что уже при 2hλ > 0,6 практически вся энергия

падающей волны проходит в клинообразную часть волновода.

Рис. 10.20. Кривые направленности RI(0) (θ) при разных величинах 2h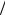λ :

а — θ0 = 90°; б — θ0 = 25°

Рассмотрим угловое распределение интенсивности звука в клино- образном волноводе. На рис. 10.20 представлены кривые направлен- ности по интенсивности при угле раскрыва θ0 = 90° (рис. 10.20, а) и θ0 = 25° (рис. 10.20, б). Падающей волной в области I является нуле- вая мода (q = 0). Характеристика кривых — это величина отношения 2h/λ, как видим, при ее увеличении кривая направленности обост- ряется. Это понятно, ведь величина 2h/λ определяет физический размер источника, который излучает звук в клинообразный волновод. Поэтому, естественно, увеличение 2h/λ приводит к обострению кривой направленности.

Интересный эффект наблюдается при относительно небольших уг- лах раскрыва волновода. Так, при θ0 = 25° (рис. 10.20, б), 2h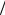λ ≈ 0,8...1,0 имеем уменьшение потока звуковой энергии вдоль оси

волновода (θ = 0°). Понятно, что это явление обусловлено амплитудно- фазовым соотношением возбужденных в клинообразном волноводе мод.

На рис. 10.21 представлены кривые направленности в клинооб- разном волноводе, когда поле падающей волны задается первой сим- метричной модой области I (q = 1, 2h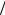λ =1,1). Как видим, для малых

углов раскрыва (θ0 < 30°) сохраняется практически то же угловое рас- пределение давления, что и у падающей волны. При увеличении угла

649

раскрыва вид кривой существенно изменяется. Практически звук вдоль оси волновода не излучается. Основная энергия прошедшей волны локализуется вблизи границ волновода.

Рис. 10.21. Кривые направленности RI(1) (θ) при разных углах раскрыва θ0

(2hλ =1,1) :

1 — θ0 = 15°; 2 — θ0 = 30°; 3 — θ0 = 40°; 4 — θ0 = = 50°; 5 — θ0 = 90°; 6 — θ0 = 130°

Такое явление обусловливает естественный вопрос: как быстро происходит преобразование энергетических потоков в клинообразном волноводе. Для ответа на этот вопрос приведем исследование вектор- ного поля интенсивности в окрестности границы раздела плоскопа- раллельного и клинообразного волноводов. Проекции вектора интен-

сивности I = {Ix ,Iy } на оси декартовой системы координат xOy (см.

Определив проекции Iх и Iу, можно построить вектор интенсивности I. На рис. 10.22 представлены поля вектора интенсивности на гра- нице раздела плоскопараллельного и клинообразного волноводов. Длина каждой стрелочки определяет относительное значение модуля вектора интенсивности, ее направление — направление потока энер- гии, а начало стрелочки — точку звукового поля, в которой опреде-

лялся вектор интенсивности.

650