Основы_акустики_Гринченко_Вовк

Рис. 11.18. Резонансные кривые диссипативного нелинейного осциллятора с жесткой нелинейностью

Напомним, что величина Q — это соотношение между резонанс- ной амплитудой линейных колебаний хл и статическим смещением хст (см. (2.68)), т.е. Q = xл/хст, а ε = (хст/d)2. Таким образом, величину

можно рассматривать как меру нелинейности осциллятора в облас- ти максимума амплитуды колебаний.

Если εQ 2 << 1, то координаты точки M (11.123) можно определить по следующим упрощенным формулам:

Частота максимальной амплитуды колебаний γm немного смещена влево от частоты γ . Но, если Q 1 можно считать, что γm ≈ γ . Итак,

частота γm не совпадает с собственной частотой линейной системы

γ= 1. Это следствие нелинейности системы. На рис. 11.18 величина

ω/ω 0 соответствует относительному сдвигу частоты максимальной амплитуды колебаний относительно частоты резонанса линейной сис-

761

темы ω 0. При условии Q 1, используя формулу (11.125), можно запи- сать следующее равенство:

Как видим, величина ω пропорциональна степени нелинейности сис- темы. Отметим, что в случае εQ2 1 (Q 1 ), как следует из второй формулы (11.125), максимальная амплитуда ξ1m ≈ ξ1 ≈ Q , т.е. совпадает

с амплитудой колебаний линейной системы на частоте резонанса ω 0. Рассматривая далее свойства кривой отклика, особое внимание

следует уделить участку кривой, где для одного γ 2 имеем три значе- ния |ξ1| (рис. 11.19). При этом очень важно, с какой стороны подхо- дить к области неоднозначности. Двигаясь со стороны низких частот, приходим в точку D1 , потом система скачкообразно переходит в точ-

ку D1′ , а дальше следуем однозначно вдоль кривой. Если двигаться со

стороны высоких частот, то приходим в точку D2; потом система скачкообразно переходит в точку D2′ , a далее следуем однозначно

вдоль кривой. Такое поведение осциллятора наблюдается и в экспе- рименте. Итак, на участке кривой D1D2 удержать систему невозмож- но, т.е. возникает неустойчивое колебательное движение — любого малого отклонения достаточно, чтобы система скачком изменила свое состояние.

Рис. 11.19. График нелинейного резонанса. Стрелки показывают направле- ние движения вдоль резонансной кривой при изменении частоты внешнего воздействия

Таким образом, неоднозначность поведения системы зависит от начальных условий: от того, с какой стороны по оси частот прибли-

762

жаемся к области неустойчивого движения D1D2. Другими словами, система помнит свое предыдущее состояние и, исходя из этого, сле- дует или вдоль ветви D2′O , или вдоль — D1′O′ . В этом проявляется

особенность нелинейного мира. При уменьшении параметра нелиней- ности ε (например, вследствие уменьшения амплитуды внешней си- лы F0) область неустойчивого движения будет сокращаться до тех пор, пока при некотором значении ε точки D1 и D1′ не совпадут (рис.

11.17).

Интересно сравнить результаты приближенного анализа с дина- микой исходной системы (11.110). Для этого нужно численно решить на ЭВМ дифференциальное уравнение (11.110) и сравнить решение с аналитическими результатами, отметив при этом характерные осо- бенности нелинейного резонанса. Величина, которую нужно сравнить с аналитическими результатами — это амплитуда колебаний в уста- новившемся режиме. Эту величину будем определять путем числен- ного решения уравнения (11.110).

Зададим некоторое отрицательное значение параметра (на рис. 11.17 = –3) и произвольные начальные условия для ξ и dξ/dτ (пусть ξ(0) = 0 и dξ(0)/ dτ = 0). Численно решением на ЭВМ уравнение (11.110) до момента установления стационарного режима колебаний. При этом параметры ε и γ следует выбирать в соответствии с заданным безраз- мерными величинами P = 3εQ3/4, = (γ2 – 1)Q и Q. На рис. 11.20, а представлена временная зависимость решения уравнения (11.110) ξ(τ)

при = –3, Р = 3,2 и Q = 30.

Итак, определив амплитуду ξ0 колебательного процесса ξ(τ) в уста- новившемся режиме, обозначим ее на графике точкой с координата-

зонансная кривая, полученная аналитическим путем. Далее придав некоторое приращение величине , повторим численное решение уравнения (11.110) с начальными условиями, которые берутся как следствие установившихся колебаний для предыдущей точки. Тем самым получим следующую точку на графике и т.д. Таким образом, сначала проходим весь интервал изменения параметра в одном на- правлении, а потом будем двигаться вдоль оси в противоположном направлении.

На рис. 11.20, б, в приведены результаты расчетов для Р = 3,2, Q = 30. Сплошная кривая соответствует формуле (11.122), точки, обо- значенные кружками, представляют численные результаты решения уравнения (11.110), полученные при движении вдоль резонансной кривой слева направо (рис. 11.20, б) и справа налево (рис. 11.20, в). Как видим, во-первых, качественное описание явлений при нелиней- ном резонансе подтверждается, наблюдается неоднозначность пове-

763

дения системы в зависимости от начальных условий и ее скачкооб- разные переходы. Во-вторых, имеем целиком удовлетворительное ко- личественное соответствие.

Рис. 11.20. Пример нелинейного резонанса:

а — зависимость ξ(τ), которая получена путем численного решения уравне- ния (11.110) при = –3, Р = 3,2; Q = 30; б, в — сопоставление приближенных аналитических результатов (сплошная кривая) согласно формуле (11.122) и численных расчетов (кружки) уравнения (11.110) (кружками обозначены точки, полученные при движении вдоль резонансной кривой слева направо (б) и справа налево (в))

Рассмотренные выше явления в колебательной системе называют нелинейным резонансом. О нем можно говорить как об основном ре- зонансе, поскольку, как оказывается, резонансные явления в нели- нейной системе могут наблюдаться не только в области собственной частоты ω 0.

764

11.12.2. Резонанс на гармониках и субгармониках

В нелинейной системе при гармоническом внешнем воз- действии процесс колебаний не является чисто гармоническим и имеет гармонические компоненты высших частот, кратные частоте внешнего воздействия. Поэтому, если частота одной из гармониче- ских компонент, которые возникли в результате нелинейности систе- мы, близка к собственной частоте системы, то амплитуда этой ком- поненты может существенным образом увеличиться, т.е. имеем резо-

нанс на гармониках.

Рассмотрим уравнение (11.117) для консервативного осциллятора, учитывая при этом “условность”, о которой выше шла речь. Понятно, что если для частот внешнего воздействия ω, близких к ω0, справедливо соотношение |ξ3 | |ξ1| (ведь ε 1), то для других частот ω такое усло-

вие может не выполняться. Разделив (11.117) на ξ3, перепишем вы- ражение в следующем виде (с вариантом жесткой нелинейности):

Рис. 11.21. Резонансная кривая для амплитуды третьей гармоники

Как и для уравнения основного резонанса (11.121), можно постро- ить кривую (см. рис. 11.21), которая представляет зависимость моду- ля амплитуды третьей гармоники |ξ3| от безразмерной частоты 3γ = 3ω /ω 0. Поведение резонансной кривой показывает, что значи- тельную амплитуду утроенной частоты 3ω можно наблюдать не при 3ω ≈ ω 0, а при 3ω > ω0, что требует выведения рабочего режима сис- темы в эту область частот. Действительно, как следует из (11.127), при

765

возможен выход на ветвь А, где амплитуда колебаний утроенной час- тоты может стать достаточно существенной. Выход системы на дан- ный режим возможен за счет постепенного изменения частоты внешней силы, например, начиная с ω = ω 0/3. Подобная ситуация для основного резонанса представлена на рис. 11.18.

Как следует из рис. 11.21, возможно существование различных режимов колебаний утроенной частоты (ветви А и В) и установив- шийся режим зависит от начальных условий и ”истории” системы. Эта особенность аналогична соответствующим свойствам для основ- ного резонанса. Естественно учет демпфирования внесет понятные изменения в ход резонансной кривой.

Нелинейные колебательные системы имеют также свойство гене- рировать субгармоники, т.е. колебания, частоты которых связаны с частотой внешнего воздействия ω соотношением ωn = ω /n, n = 2,3,4,… Возникновение этих колебаний можно объяснить, исходя из следующих физических рассуждений. Как известно, для линейного уравнения

ξ + ω20ξ = F0 cos(mω0t) общее решение имеет вид суммы двух слагае-

мых: одно из них описывает вынужденные колебания системы с час- тотой mω 0, а второе соответствует свободным колебаниям с частотой ω 0, причем последние зависят от начальных условий. Однако при на- личии в линейной системе демпфирования, свободные колебания за- тухают и в системе остаются чисто вынужденные колебания с часто- той внешнего воздействия ω = mω 0. В нелинейной системе все гармо- ники взаимосвязаны, так что ни одна из них не может измениться, не влияя на другую; поэтому колебания с частотой mω 0 могут порож- дать и поддерживать гармонику с частотой ω 0, а отсюда возможно возникновение явления резонанса.

Снова вернемся к консервативному (Q → ∞) осциллятору (11.110) с жесткой кубической нелинейностью, учитывая “условность” дальней- шего анализа. В системах этого типа чаще всего наблюдаются суб- гармонические колебания с частотой ω /3, где ω — частота внешнего воздействия. Обратим внимание именно на эту субгармонику.

Исходя из физических соображений, учтем наличие субгармоники в отклике системы и запишем решение в виде

ξ(t) = ξ1/3cos(γτ/3) + ξ1cos(γτ) + …

В первом приближении будем использовать два первых слагаемых этого выражения. После подстановки решения ξ(t) = ξ1/3cos(γτ/3) + +ξ1cos(γτ) в уравнение (11.110) (при Q → ∞) его левая часть будет иметь вид, подобный соотношению (11.114), а именно: A1/3cos(γτ/3) + A1cos(γτ) + …, где A1/3 и A1 — функции амплитуд ξ1/3 и

766

ξ1. Отсюда в первом приближении для выполнения уравнения дви- жения получим A1/3 = 0 и A1 = 1, или

Прежде всего, следует отметить, что системе уравнений (11.128), (11.129) удовлетворяет решение ξ1/3 = 0, которому соответствуют вы- нужденные колебания с частотой внешней силы. Действительно, если положить ξ1/3 = 0, то уравнение (11.128) будет выполняться всегда, а (11.129) будет иметь вид уравнения (11.121), которое получено как первое приближение при исследовании основного резонанса.

Если допустить, что ξ1/3 ≠ 0, то уравнение (11.128) можно разде- лить на ξ1/3. Тогда оно станет квадратичным уравнением относитель- но как ξ1/3, так и ξ1. Решив его относительно ξ1/3, получим

Для того чтобы ξ1/3 была действительной величиной и имела физиче- ский смысл, необходимым является следующее условие:

Таким образом, если частота вынуждающей силы будет увеличивать- ся, то субгармонические колебания возникнут только тогда, когда ве- личина γ достигнет значения γ*, при котором амплитуда колебаний будет равна ξ1/3 = –ξ1/2.

Если полагать, что ε << 1, то формула (11.130) примет простой вид:

а условие (11.132) можно представить в виде: γ > γ0 = 3. Для получе- ния соответствующего приближения основной амплитуды ξ1, следует решить уравнение (11.129), содержащее в себе все слагаемые, кроме

3ξ13 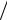4 , которое намного меньше других слагаемых. Тогда с учетом

(11.133) имеем

767

Отметим, что, как следует из (11.133) и (11.134), при γ2 = 9 + 273 ε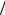4

амплитуда ξ1 равна нулю. Это соответствует ситуации, когда вынуж- денные колебания с частотой ω практически полностью переходят в субгармонические колебания с частотой ω /3. Как и для основного ре- зонанса системы и резонанса на гармониках, следует особенно отме- тить важность соответствующих начальных условий для возникнове- ния субгармонических колебаний. Но если субгармонические колеба- ния возникают, то их амплитуда может значительно превышать ам- плитуду основных колебаний, частота которых равна частоте внеш- ней силы ω.

При проведении анализа не учитывались силы демпфирования. Понятно, что их наличие уменьшает амплитуду субгармонических ко- лебаний, а при значительном демпфировании субгармонические ко- лебания вообще могут не возникнуть.

Таким образом, реакция нелинейной системы на воздействие си- нусоидальной силы в общем случае не является гармонической. Нали- чие в отклике системы гармоник или субгармоник — характерный признак нелинейной системы. Возможны даже резонансные явления на частотах гармоник или субгармоник. Все это очень важно в кон- кретных ситуациях. Приведем два примера.

Как известно, наше ухо является нелинейной системой. Нелиней- ность слухового аппарата проявляется в том, что при действии на ба- рабанную перепонку довольно громкого синусоидального звука с час- тотой ω в нем появляются гармоники с частотой 2ω, 3ω и т.д. По- скольку в сигнале, действующем на ухо, этих гармоник нет, то их на- звали субъективными гармониками. Их наличие определяется мето- дом звукового зонда: если к звуку, под действием которого возникают субъективные гармоники, прибавить второй звук, частоту ω и гром- кость которого можно изменять, то при приближении частоты ω к частоте субъективной гармоники 2ω на фоне громкого основного зву- ка можно услышать биения, которые возникают вследствие взаимо- действия звука зонда и субъективной гармоники (см. параграф 2.7). Наиболее резкие биения прослушиваются при условии равенства ам- плитуд звука зонда и субъективной гармоники. Поэтому, отрегулиро- вав амплитуду давления звука зонда до получения более четких бие- ний, можно оценить амплитуду субъективной гармоники. При увели- чении интенсивности звука субъективные гармоники резко увеличи- ваются и могут даже превысить интенсивность основного тона.

768

Другой пример можно привести из области электроакустики, ко- торая занимается вопросами приема и излучения звуковых волн в воздухе. Все электроакустические аппараты (например, микрофоны и громкоговорители) являются линеаризованными системами, т.е. ха- рактеризуются примерно линейными соотношениями входных и вы- ходных величин. Превышение определенных границ этих величин приводит к появлению гармоник и субгармоник в выходном сигнале по отношению к гармоническому входному сигналу. Слух человека очень чувствителен к такому изменению сигнала, поэтому при проек- тировании громкоговорителя в этом аспекте выдвигаются жесткие требования. При существенной нелинейности громкоговорителя по- являются разные посторонние звуки, хрип, звон и т.п.; они сопрово- ждают работу громкоговорителя, когда его колебательная система на- ходится в области неустойчивого движения.

11.13. Хаос при вынужденных колебаниях нелинейного осциллятора

С древних времен считалось, что умение предсказывать – удел мудрецов, и вместе с тем, предвидение – это одна из основных целей науки. Развитие математики существенно расширило возмож- ности исследователей в проведении научного прогноза. Оказалось, например, что движение небесных тел можно рассчитывать, решая дифференциальные уравнения, которые могут быть достаточно сложными, и для их решения нужно будет приложить немало усилий. Такая работа увлекла ученых на многие годы и, казалось, единствен- ным препятствием будут чисто математические трудности, которые со временем преодолеют.

Однако с развитием науки возникло понимание того, что нельзя сделать, какие цели не стоят перед научным исследованием. Так, с появлением термодинамики стало понятно, почему никогда не по- строят вечный двигатель. Квантовая механика показала, что мы принципиально лишены возможности измерить с заранее заданной точностью одновременно координату и импульс элементарной части- цы. На множество непреодолимых барьеров указала теория относи- тельности. По сути, понимание новых ограничений стало признаком фундаментальных теорий.

В этом ряду важное место занимают работы последних лет, свя- занные с предсказуемостью. Стимулом к таким исследованиям по- служила работа американского метеоролога Лоренца , опубликован- ная в 1963 году. Лоренц поставил перед собой вопрос: почему при наличии мощных ЭВМ нельзя дать надежный, достаточно долгосроч-

Лоренц (Lorenz) Едвард Нортон (1917—2008) — американський математик.

769

ный прогноз погоды. Он предложил простую модель, которая описы- вала динамику атмосферы, просчитал её на ЭВМ и, получив резуль- тат, не отмахнулся от него как от ошибки вычислений, а отнесся очень серьезно. Этот результат – возникновение хаотических, напо- минающих случайные, колебаний. При этом модель Лоренца была де- терминированной, т.е. в уравнениях её динамики полностью отсутст- вовали случайные параметры.

Таким образом, в системе, где будущее однозначно определяется прошлым, Лоренц обнаружил конечный горизонт прогноза. Это явле-

ние получило название детерминированного (динамического) хаоса.

Вслед за работой Лоренца начались интенсивные исследования дан- ного явления.

Оказалось, что динамический хаос свойственен не только физиче- ским нелинейным системам. В настоящее время хаосу посвящено много книг и обзоров, большое число статей опубликовано в ведущих научных журналах мира по математике, физике, химии, биологии, астрономии, экономике и других. Особо следует отметить тот факт, что явление детерминированного хаоса было обнаружено в системах

смалым числом степеней свободы. Конечно, если исследовать систему

сбольшим числом степеней свободы, например газ, жидкость, то даже интуитивно мы понимаем, что предусмотреть траекторию движения микрообъема такой среды невозможно. Но сейчас речь идет о систе- мах с малым числом степеней свободы!

Как свидетельство таких перемен в науке процитируем торжест- венное заявление, с которым выступил в 1986 г. всемирно известный

английский гидромеханик сэр Дж. Лайтхилл , бывший в то время президентом Международного союза теоретической и прикладной механики: “Тут я должен остановиться и снова выступить от име- ни широкого всемирного братства тех, кто занимается механикой. Мы все глубоко сознаем сегодня, что энтузиазм наших предшествен- ников по поводу великолепных достижений ньютоновской механики побудил их к обобщениям в этой области предсказуемости, в кото- рые до 1960 г. мы все охотно верили, но которые, как мы теперь по- нимаем, были ложными. Нас не покидает коллективное желание признать свою вину за то, что мы вводили в заблуждение широкие круги образованных людей, распространяя идеи о детерминизме систем, удовлетворяющих законам движения Ньютона, – идеи, ко- торые, как выяснилось после 1960 г., оказались неправильными.”

Лайтхилл (Ligthill) Джеймс (1924—1988) — английский физик.

Ligthill J. The Recently Recognized Failure of Predictability in Newtonain Dynamics // Proceeding of the Royal Society. – 1986. – P. 35–50.

770