Основы_акустики_Гринченко_Вовк

батичности волнового процесса. Перед тем как провести его анализ попробуем ответить на следующий вопрос. Как определить локальную фазовую скорость, если уравнение состояния для среды отличается от уравнения для идеального газа? Для этого следует рассмотреть уравне- ние состояния в виде ряда (12.6). В задачах нелинейной акустики, где числа Маха невелики (М ≈ 10–4…10–2), обычно ограничиваются двумя членами в ряде (12.6). Тогда уравнение состояния (12.5) имеет вид

Как известно, постоянная А — линейный коэффициент упругости, то- гда постоянную В можно определить как нелинейный коэффициент упругости. Единицы измерения коэффициентов А и В одинаковы. Очевидно, отношение В/А характеризует степень нелинейности сре- ды. Так, для воздуха В/А ≈ 0,4, для воды В/А ≈ 4,2 ... 6,1 (при темпе- ратуре t = 0…100°C). С этой точки зрения жидкости более нелиней- ные, чем газы.

Понятно, что мощные нелинейные волны, которые возникают при взрывах и разрядах, где число Маха близко к единице, требуют для своего описания других законов распространения, но эти случаи мы не рассматриваем.

Дифференцируя (12.28) по плотности, определяем значение мест- ной скорости звука в таком виде:

(12.29) и (12.19)). Поскольку согласно (12.2) ρ /ρ0 = υ/с, то, учитывая,

что М << 1, переписываем (12.30) в виде

Как видим, зависимость местной скорости звука с от переменной ве- личины υ обусловлена только упругой нелинейностью среды, которая

определяется соотношением В/(2А). Величину εф = В/(2А) называют

коэффициентом физической нелинейности.

Тогда выражение для локальной скорости приобретает вид

называют коэффициентом акустической нелинейности. Величина εг =1 есть коэффициент геометрической нелинейности.

Принимая во внимание (12.32), записываем уравнение (12.13) для

Для адиабатического процесса коэффициент ε легко получить из формул (12.29) для постоянных А и В и уравнения адиабаты Пуассона

(12.17):

Итак, для газов коэффициент ε выражается через показатель адиа- баты γ = Ср/СV. Например, для воздуха (γ = 1,4) имеем ε = 1,2. В случае жидкостей ε измеряется экспериментально. Так, для воды ε = 3,1...4,1 при изменении температуры от 0 до 100 °C. Измерения показали, что для однородных сред (в том числе и твердых тел) величина ε практи- чески не превышает 101.

Однако для структурно-неоднородных сред экспериментально бы- ли получены значения ε 102…103... Так, наличие парогазовых пу- зырьков в воде резко повышает нелинейные свойства среды. Причи- ны появления таких больших значений коэффициента ε иные, чем в случаях физической и геометрической нелинейностей. В данном слу- чае говорят о третьем типе нелинейности — “структурном” [42].

Перепишем выражение (12.26) для нелинейной волны, воспользо- вавшись формулой (12.32) для локальной скорости:

Выражение (12.36) показывает, что относительно неподвижной сис- темы координат волна распространяется со скоростью

т.е. скорость перемещения точек профиля волны разная. Те точки, в которых υ > 0, перемещаются со скоростями сл > c0 и соответствуют областям сжатия. Наоборот, в области растяжения υ < 0 , и поэтому эти области перемещаются со скоростями сл < с0. Точки, которым со-

ответствует фаза нулевого сжатия, распространяются со скоростью

сл = с0 (рис. 12.1, а).

Рис. 12.1. Изменение “профиля” исходной гармонической волны в процессе ее распространения

Таким образом, начальный “профиль” волны в процессе распро- странения деформируется. На рис. 12.1, б представлены изменения, происходящие в профиле исходной гармонической волны. Пренебре- жение нелинейными членами в уравнениях акустики (12.3)-(12.5) приводит к линейному волновому уравнению, решением которого яв- ляются волны, не изменяющие форму при распространении. Таким образом, деформирование исходного профиля волны связано именно

ссохранением этих нелинейных членов.

Впроцессе изменения профиль волны приобретает форму, близ-

кую к пилообразной, и далее зависимость υ(х) становится неодно- значной (штриховая линия на рис. 12.1, б). Такая форма может реа- лизоваться, например, для волн на поверхности воды в зоне прибоя. Но для плоской звуковой волны профиль, изображенный штриховой линией на рис. 12.1, б физического смысла не имеет, поскольку зна- чению координаты х соответствуют три значения колебательной ско- рости (давления, плотности). Полученный результат говорит о том, что в уравнении (12.13) не были учтены те или иные факторы, способные

813

остановить переход к неоднозначной зависимости υ(x ). К таким

факторам, как мы узнаем далее, принадлежат диссипация и диспер- сия. Поэтому в данной ситуации мы будем говорить, что в профиле волны возникает поверхность разрыва, т.е. скачок величин, которые характеризуют звуковую волну (давление, плотность, колебательная скорость). О разрыве иначе говорят как об ударной волне. Понятно, что в такой ситуации волна перестает быть простой.

12.2.2. Графический анализ деформации профиля волны Римана

Формула (12.36) представляет собой неявную функцию. Однако с помощью графических построений можно проанализиро- вать поведение простой волны. Для этого зададим конкретный вид начального возмущения. Пусть при х = 0 имеем гармоническую зави- симость колебательной скорости υ = υ0sin(ωt). Согласно (12.36) дефор- мация гармонического профиля описывается соотношением:

Изменение профиля волны удобно наблюдать в сопровождающей системе координат, т.е. системе, которая двигается вместе с волной со скоростью с0. Понятно, что для линейной волны ее профиль в со- провождающей системе координат будет неизменным. В сопровож- дающей системе координат время τ = t – x/c0. Тогда

Первое слагаемое в аргументе функции синуса описывает распро- странение волны и связанное с этим запаздывание сигнала, а вто- рое — постепенное изменение профиля волны. При М = υ0/с0 → 0 име- ем плоскую линейную волну, параметры которой зависят только от τ. Выражение (12.38), которое неявно определяет υ , может быть пред- ставлено в виде соотношения относительно ωτ:

Проанализируем данное выражение графически. На рис. 12.2, а построены графики функций ωτ = arcsin(υ/υ0 ) и второго слагаемого

правой части выражения (12.39) для двух разных значений х1 и х2 параметра х (x2 > x1). Интересующая нас деформация профиля пред-

814

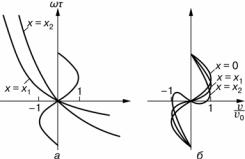
ставлена на рис. 12.2, б путем сложения графиков начального возму- щения ωτ = arcsin(υ/υ0 ) и соответствующей гиперболы.

Рис. 12.2. Графический анализ деформации профиля волны (x2 > x1)

Как следует из рисунка, области сжатия и разряжения изменяют- ся по-разному. Область разряжения деформируется сильнее. Дефор- мация профиля волны носит накопительный характер, т.е. увеличи- вается с увеличением пройденного волной пути. Деформация профи- ля волны тем сильнее, чем больше число Маха М. Поэтому, значение М может служить мерой нелинейности акустического волнового процес- са.

12.3. Методы получения приближенных уравнений нелинейной акустики

Понимание закономерностей нелинейных волновых про- цессов невозможно без теоретического исследования. Такое исследо- вание базируется на анализе уравнений акустики для тех или иных моделей реальной среды, где наблюдается волновой процесс. Однако даже для самой простой модели — идеальной среды (см. раздел 4) — нелинейные уравнения акустики довольно сложные, и решение воз- можно только в отдельных случаях, одно из которых (простая волна) рассмотрено в параграфе 12.2. В такой ситуации необходимыми и перспективными являются приближенные методы анализа. Суть их состоит в том, чтобы в некотором диапазоне параметров волнового процесса заменить точные уравнения приближенными и сделать это таким образом, чтобы не исказить главные особенности исследуемого волнового процесса, и при этом не касаться несущественных деталей. Такая работа нуждается в глубоком знании физики исследуемых вол- новых процессов и даже акустической интуиции.

Пути упрощения точных уравнений могут быть определены на ос- нове анализа простых примеров. В частности, в предыдущем пара-

815

графе было отмечено, что процесс распространения волны большой амплитуды условно разделяется на два процесса: процесс распро- странения волны без изменения профиля и процесс деформации профиля волны. Понятно, что точные уравнения целостно описывают процесс распространения-деформации. Успех при упрощении точных уравнений возможен, если попытаться отделить математическое опи- сание деформации профиля волны от описания процесса распро- странения волны. Это удается сделать в двух случаях:

1)когда деформации профиля волны представляют собой малые поправки к исходной волне;

2)когда изменение профиля волны происходит медленно. Факторы “малости” и “медленности” позволяют выделить в уравнени- ях малые по величине слагаемые и пренебречь ими. Итак, мы осмыс- лили возможность существования двух методов получения прибли- женных уравнений акустики. Ниже рассмотрим их.

12.3.1. Метод последовательных приближений

Изучая распространение нелинейной волны, мы убеждаем- ся, что изменение профиля волны накапливается постепенно в процес- се распространения, причем тем медленнее, чем меньше амплитуда первоначального сигнала. Если рассматривать сигналы “умеренной” амплитуды на небольших расстояниях их распространения, то в пре- делах этого участка нелинейность волнового процесса приводит к по- явлению только небольших изменений в профиле линейной волны. То- гда функции, описывающие волну: P(x,t), υ(x,t), ρ(x,t), можно записать в виде рядов:

P= P0 + p′ + p′′ +...,

υ= υ′ + υ′′ +...,

где Р0, ρ0 — параметры невозмущенной среды; р′, υ′, ρ′ — переменные, связанные с распространением линейной

волны; если ограничить ряд этими величинами, то получим первое (или линейное) приближение; о параметрах р′, υ′, ρ′ говорят как о ве-

личинах первого порядка малости; р″, υ″, ρ″ — величины второго порядка малости (или квадратич-

ные добавки), при ограничении ряда этими величинами говорят о втором приближении и так далее. Существенным моментом являются выполнение соотношений Р0 >> р′ >> р″ >> р″′ и т.д.

Метод последовательных приближений дает возможность получить достаточно простые уравнения для каждой из величин (р′, р″ и т.д.) отдельно. Причем каждая из величин следующего порядка может

816

вых моментов преобразований, которые здесь выполняются. Дело в том, что величины разных порядков малости (они выделяются квад- ратными скобками) не могут уравновесить одна другую, поэтому сле- дует приравнивать их к нулю каждую отдельно. Тогда получаем сле- дующие системы уравнений относительно р′,υ′, ρ′ и р″, υ″, ρ″:

где

F1 = −ρ′ ∂υ∂t′ − ρ0υ′ ∂∂υx′, F2 = −υ′ ∂ρ∂x′ − ρ′ ∂υ∂x′,

Продифференцируем уравнения, записанные в первой строке, по х, а уравнения во второй строке по t, а затем вычтем одно из другого. В результате, приходим к волновому уравнению для линейной волны

p′(x,t ) и для слагаемого второго приближения p′′(x,t ):

где

818

Используя связь между p′, υ′ и ρ′ (см. (12.46)), можно привести вы- ражение (12.51) к виду

значений кинетической и потенциальной энергий в “линейной” волне.

Решая уравнение (12.49), находим p′(x,t ) — волна первого при-

ближения, или линейная волна. Зная параметры р′, υ′ этой волны, по- лучаем правую часть уравнения (12.50) и, решая его, определяем до- бавку второго приближения. Поскольку уравнение (12.50) — волно- вое, добавка представляет собой также волну, распространяющуюся, как и линейная волна, со скоростью с0.

Интересной является следующая интерпретация правой части уравнения (12.50). Обычно, правая часть уравнения определяет неко- торое постороннее воздействие, связанное с источником энергии. Это

позволяет рассматривать волну p′′(x,t ) как результат излучения не- которой системы источников, распределенных по объему среды, при- чем сами источники будто бы рождены линейной волной p′(x,t ) . Ин-

терпретация правой части уравнения (12.50), как системы источни- ков, не является обязательной, но она очень полезна, ведь позволяет использовать в дальнейшем анализе опыт и интуицию, полученные при изучении явлений линейной акустики.

Аналогично можно получить волновые уравнения и для слагаемых более высоких приближений, причем оказалось, что правые части уравнений определяются через параметры добавок с более низкими номерами. Другими словами, эти уравнения образуют рекуррентную систему.

12.3.2. Метод медленно изменяющегося профиля

Метод последовательных приближений не приводит к гру- бым ошибкам до тех пор, пока каждая следующая поправка на поря- док меньше предыдущей, т.е. р″ << р′ << Р0. В ходе накопления нели- нейных искажений при распространении звука это условие перестает выполняться, что и ограничивает область применения метода после-

819