Основы_акустики_Гринченко_Вовк

в свободном пространстве. На рис. 10.26 имеем полупространство с жесткой или мягкой границей. Поэтому, волны типа

p = hv(1) (kr )Pv (cos θ) должны удовлетворять граничным условиям на

поверхности экрана, чего можно достичь правильным выбором вели- чины v. Граничные условия на жестком экране требуют равенства нулю производной от давления по нормали, что эквивалентно произ- водной по углу θ при θ = π2, т.е. ∂p∂θ = 0 при θ = π2 . Отсюда полу-

Таким образом, поле давления в области II представляет собой су- перпозицию волн hv(1)n (kr )Pvn (cos θ), т.е.

коэффициентов Bn можно удовлетворить условия сопряжения звуко- вых полей на границе раздела областей I и II.

Теперь построим общее решение для области I. Оно будет состо- ять из двух слагаемых pI(1) и pI(2) , причем одно из них должно обес-

печить выполнение условий сопряжения полей на границе раздела областей I и II, а второе — граничное условие на поверхности диска.

Что касается первого слагаемого pI(1) , то, очевидно, оно имеет вид

(10.108), только вместо радиальных функций h2(1)n (kr ) (выбираем на- бор функций для жесткого экрана), описывающих бегущие волны,

661

Предлагаем читателю самостоятельно получить аналогичные формулы для диска в акустически мягком экране.

Построенное решение позволяет исследовать различные характе- ристики звукового поля диска. В начале исследуем сходимость полу- ченного решения, определив невязку при выполнении условий со- пряжения звуковых полей на границе областей I и II. Средние значе-

ния невязки по давлению δp = (pI − pII )/ pII и колебательной скоро-

сти δυ = (υrI − υrII )/ υrII на границе областей I и II приведены в табли- це 1 (в расчетах величина ka = 7 ). При проведении процедуры редук- ции бесконечной системы алгебраических уравнений индекс сумми- рования, во всех определенных выше суммах, изменялся от 0 до N .

Следует отметить, что у края диска (r = a , θ = 90 ) невязка несколько возрастает (особенно для акустически мягкого экрана), что, в рамках рассматриваемой математической модели, является совершенно ес- тественным и прогнозируемым результатом. Приведенные расчеты дают представление о поточечной сходимости построенного решения в ближнем поле диска.

Таблица 1.

Обратимся к интегральной оценке процесса сходимости, путем сравнения акустической мощности на поверхности диска Ρ1 (область

I) и акустической мощности в дальнем поле диска Ρ2 (область II). Ана- логичные расчеты для невязки по мощности δΡ = (Ρ1 − Ρ2 )/Ρ2 пред-

ставлены в таблице 2. Как видно, наблюдается вполне удовлетвори- тельная сходимость построенного решения.

Таблица 2

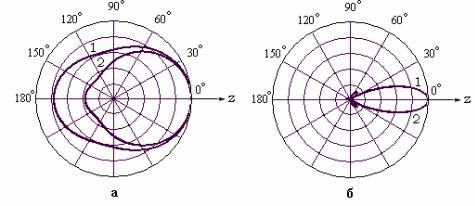
Рис. 10.27. Диаграммы направленности диска в экране:

а – ka =1, б – ka = 7 ;

1 – акустически жесткий экран, 2 – акустически мягкий экран

Перейдем к анализу численных данных о характеристиках звуко- вого поля диска. На рис. 10.27 приведены диаграммы направленно- сти по давлению при двух величинах ka . При малом волновом разме- ре диска (ka =1, рис. 10.27, а) формы диаграмм существенно зависят от свойств экрана. Если при жестком экране диск практически нена- правлен (излучает как монополь), то при мягком он существенно на- правлен (излучает как диполь). При большой величине ka (ka = 7 , рис. 10.27, б), для обоих вариантов экрана, с графической точностью диаграммы направленности совпадают. Это обусловлено тем, что при достаточно большом волновом радиусе диска звуковая энергия в дальнем поле концентрируется в области осевого направления и, как следствие, влияние свойств экрана практически несущественно.

Обратимся теперь к такой важной интегральной характеристике процесса излучения звука как импеданс излучения. Интересно срав- нить полученное решение с известными результатами, которые полу- чены благодаря интегральным соотношениям (см. раздел 9). Согласно

диска S. В соответствии с симметрией задачи элементом dS может служить элементарное кольцо толщиной dr (рис. 10.28), а именно, dS = 2πrdr. В таком случае имеем

Рис. 10.28. Элементарное кольцо площадью dS на поверхности диска

Подставляя (10.120) в (10.122), получаем расчетную формулу для со- противления излучения диска в жестком экране:

где

ka

en = ∫ j2n (x )xdx. (10.124)

0

Расчеты, проведенные по формулам (9.87) и (10.123) при ka ≤ 5,5, по- казывают, что при удержании шести членов ряда (10.123) кривые, которые определяют действительную и мнимую части сопротивления излучения, с графической точностью совпадают.

Рис. 10.29. Безразмерный импеданс излучения диска в бесконечном эк- ране: 1,2 – действительные и 1,2′ ′ – мнимые части импеданса излучения, 1,1′ – акустически жесткий экран, 2,2′ – акустически мягкий экран

666

На рис. 10.29 показаны действительная R′ = Re(Zи /ρcS) (кривые 1,2) и мнимая X ′ = Im(Zи /ρcS) (кривые 1,2′ ′) части безразмерного им-

педанса излучения диска в акустически жестком и акустически мяг- ком экранах как функции волнового радиуса диска ka . Числовые данные нормированы к величине ρcS — сопротивлению излучения

диска в бесконечной трубе с жесткими стенками. Как видим, если при больших значениях ka ход кривых для случаев жесткого и мяг- кого экранов сближается, то при малых значениях ka поведение дей- ствительных частей сопротивления излучения существенно отличает- ся. Это обусловлено тем, что диск в мягком экране эквивалентен ос- циллирующему диску в свободном пространстве, что приводит при малых волновых размерах диска к так называемому “акустическому короткому замыканию” (см. в конце параграфа 7.8 и ниже п. 10.8.3).

Задача. Объясните, почему колебания диска в мягком экране эк- вивалентны осциллирующему диску в свободном пространстве, а ко- лебания диска в жестком экране эквивалентны пульсирующему диску в свободном пространстве

10.8.2. Диск в полусферическом экране

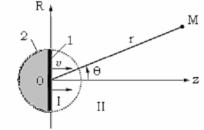
Рассмотрим теперь ситуацию, когда диск размещен не в бесконечном экране, а в экране конечных размеров. Например, практический интерес представляет диск на полусфере того же ра- диуса a (см. рис. 10.30) с акустически жесткой или акустически мяг- кой сферической поверхностью. Скорость на поверхности диска бу-

дем считать равномерной, т. е. υz (S ) = υ0 . Если, для случая диска в

бесконечном экране (рис. 10.26), диск “озвучивал” только полупро- странство, то в ситуации, изображенной на рис. 10.30, диск “озвучи- вает” уже все пространство. Поэтому область II теперь является внешностью сферы радиуса a , а поле в области I определяется вы- ражением (10.120). Тогда поле в области II следует писать в виде

∞

pII = ∑ Bnhn(1) (kr )Pn (cos θ). (10.125)

n =0

Рис. 10.30. Диск в полусферическом экране: 1 – диск, 2 – полусферический экран

667

Функциональная система уравнений, определяющая условия со- пряжения звуковых полей на границе частичных областей I и II для случая с жесткой полусферой теперь будет иметь следующий вид

Провести дальнейшие выкладки читатель сможет самостоятельно.

Рис. 10.31. Диаграммы направленности диска в полусферическом экране: а – ka =1, б – ka = 7 ; 1 –жесткая полусфера, 2 – мягкая полусфера

На рис. 10.31 представлены диаграммы направленности диска в полусферическом экране. Как видно, при малом волновом размере диска (рис. 10.31, а) влияние свойств полусферы существенно – для акустически мягкой полусферы направленные свойства выражены значительно сильнее, чем в случае акустически жесткой полусферы. В частности уровень тыльного лепестка, в случае мягкой полусферы, примерно в два раза ниже, чем в случае жесткой полусферы. При этом имеется существенное различие в диаграммах для диска на по- лусфере и в бесконечном экране (сравни рис. 10.31, а и рис. 10.27, а). При сравнительно большом волновом радиусе (ka = 7 , рис. 10.31, б) свойства полусферы практически не имеют значения и диаграммы направленности фактически совпадает с диаграммами направленно-

668

сти диска в плоском бесконечном экране (сравни рис. 10.31, б и рис. 10.27, б).

Рис. 10.32. Нормированные действительная (кривые 1,2) и мнимая (кривые 1,2′ ′) части импеданса излучения диска в полусферическом экране: 1,1′ – жесткая полусфера, 2,2′ – мягкая полусфера

Импеданс излучения диска на полусфере как функция волнового радиуса ka показан на рис. 10.32. Сравнивая эти графики с анало- гичными графиками для диска в бесконечном экране (рис. 10.29), следует отметить, что если общий характер хода кривых в целом схо- ден, то в области небольших волновых величин (ka ≤ 2 ) имеется отли- чие. Оно проявляется в том, что для диска в плоском бесконечном акустически жестком и акустически мягком экране вещественные части Zи существенно различаются, а для диска на полусфере это от-

личие незначительно.

10.8.3. Диск в конечном кольцевом экране

Как мы видели выше, осциллирующий диск (диск в мяг- ком экране), как излучатель звука, менее эффективен в области ka ≤ 2 , чем пульсирующий диск (диск в жестком экране). Относи- тельно низкая эффективность осциллирующего диска связана с тем, что на его поверхностях давление имеет разные знаки и за счет этого возникает волновой эффект, известный как акустическое короткое замыкание, который приводит к значительному снижению импедан- са излучения. Поэтому, например, громкоговоритель, диффузор кото- рого совершает осциллирующие колебания, размещают в экране, что способствует ослаблению эффекта акустического короткого замыка- ния и, как следствие, повышению импеданса излучения громкогово- рителя на низких частотах и его эффективности в целом. Ниже, на

669

примере осциллирующего диска, мы рассмотрим степень влияния кольцевого акустически жесткого экрана на его импеданс излучения.

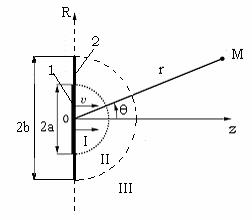
Рис. 10.33. Осциллирующий диск в кольцевом экране конечных размеров: 1 – диск, 2 – жесткий кольцевой экран

Пусть осциллирующий диск, совершающий поршневое движение, расположен в кольцевом экране (рис. 10.33), внешний радиус которо- го равен b , а внутренний равен радиусу диска a . Для осциллирую-

щего диска поверхность θ = π/2, ψ = [0,2π], r > b (пунктирные линии на рис. 10.33) является акустически мягкой. Тогда естественным об- разом возникают три частичные области: область I – r ≤ a , θ = [0,π/2];

область II – a ≤ r ≤ b , θ = [0,π/2]; область III – r ≥ b , θ = [0,π/2].

Предлагаем читателю самостоятельно записать поля в областях III и I . Поле в области II запишем в виде двух наборов частных реше- ний уравнения Гельмгольца, поскольку эта область ограничена двумя

поверхностями: θ = [0,π/2], r = a и θ = [0,π/2], r = b . Таким образом,

где y2n (kr ) – сферические функции Бесселя второго рода.

Функциональная система уравнений, определяющая условия сши- вания звуковых полей на границах частичных областей, имеет вид