Основы_акустики_Гринченко_Вовк

Выражение (10.63) является общим решением уравнения Гельмгольца для области I, т.е. его форма не изменится при любых условиях на гра- нице раздела областей I и III.

Аналогично в системе координат x′Oy′ запишем поле давления в области II, определяющее прошедшую волну через изгиб:

Решение для области III является общим. Действительно, выраже- ние (10.67) состоит из четырех рядов Фурье с произвольными коэф- фициентами, что дает возможность выполнить условия сопряжения полей на границах раздела областей I и III, II и III, а также граничные условия на акустически жестких границах области III. При этом первая сумма в формуле (10.67) за счет полноты системы функций

cos (nπx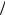h1 ), n = 0,1,2,… на отрезке y = [0,h1] гарантирует выполнение условий сопряжения звуковых областей на границе раздела областей I и III. Вторая сумма за счет полноты системы функций cos (nπy′h2 ),

n = 0,1,2,… на отрезке y′ = [0,h2] обеспечивает выполнение условий со- пряжения звуковых полей на границе раздела областей II и III. Третья сумма обеспечивает выполнение граничного условия на жесткой по-

631

верхности x = [−l,0], y = 0, a четвертая — на жесткой поверхности x′ = [0,l′], y′ = 0.

Обратите внимание на знак показателя экспонент в формуле (10.67). Он выбирается таким, чтобы волны распространялись вдоль соответствующей оси вглубь области III. В этом случае амплитуда дав- ления в неоднородных волнах будет уменьшаться от границы вглубь области III.

Условия сопряжения на границах определенных областей и гра- ничные условия на жестких поверхностях области III имеют вид

Подстановка выражений (10.63) — (10.67) в условия (10.69) с учетом формул, определяющих связь между системами координат xOy, x′Oy′:

приводит к системе функциональных уравнений. Использование свойства ортогональности системы функций cos (nπyh1 ), n = 0,1,2,...

на отрезке [0,h1], системы функций cos (nπy′h2 ), n = 0,1,2,... на отрезке [0,h2], системы функций cos (nπxl ), n = 0,1,2,… на отрезкеx = [−l,0] ,

системы функций cos(nπx′l′) , n = 0,1,2,… на отрезке x′ = [0,l′] дает

возможность провести алгебраизацию функциональной системы. В результате этого получим бесконечную систему линейных алгебраиче- ских уравнений второго рода относительно неизвестных коэффици- ентов An, Bn, Cn, Dn, En, Fn. Читатель сможет выполнить эти неслож- ные, но достаточно громоздкие преобразования самостоятельно.

Полученное решение позволяет провести анализ звукового поля в волноводе. Большое значение имеют энергетические характеристики прохождения звуковой волны через изгиб волновода. Естественно оп-

632

ределить коэффициенты прохождения W (q) как отношение среднего потока мощности волны в области II к среднему потоку мощности q-й моды, падающей на изгиб в области I:

где * — знак комплексного сопряжения. Напомним, что согласно (4.59) под знаком интеграла с точностью до постоянного множителя

1(4ωρ) записана интенсивность. После интегрирования по сечению

волновода определяем средний поток мощности. Подставляя выра- жения (10.62) и (10.65) в (10.71) и проводя соответствующие преобра- зования, получаем формулу для коэффициента прохождения q-й мо- ды через изгиб волновода:

Согласно выражениям (10.72) и (10.73) коэффициент прохождения W (q) представлен в виде суммы энергетических коэффициентов воз- мущения Wn(q) мод области II, или, иначе, выражение (10.72) можно трактовать как сумму коэффициентов трансформации q-й моды об- ласти I в моды области II. Согласно (10.73) число слагаемых N2 в формуле (10.72) равно количеству однородных (т.е. распространяю-

щихся) нормальных волн области II (для них Re(γn ) ≠ 0 ).

Аналогично, коэффициент отражения V (q), который определяется как отношение среднего потока мощности в отраженной волне к среднему потоку мощности q-й моды, падающей на изгиб в области I, представлен в виде

Согласно закону сохранения энергии должно выполняться условие

V (q) + W (q) = 1.

633

Решение бесконечной системы алгебраических уравнений можно получить методом редукции. Количество уравнений в редуцирован- ной системе определяется волновыми размерами соответствующих областей волновода h1,h2, l, l′ (рис. 10.7). В расчетах количество уч-

тенных мод, определяющих порядок системы уравнений, содержит в себе все однородные волны и несколько (три-четыре, чего оказывает- ся вполне достаточно) неоднородных. При таких условиях закон со- хранения энергии выполняется с точностью, не хуже, чем 0,1 %.

Рис. 10.8. Частотные зависимости энергетического коэффициента прохож-

дения W (0) при h1 = h2 = h :

1 — θ = 5°; 2 — θ = 45°; 3 — θ = 65°; 4 — θ = 90°

На рис. 10.8 представлены частотные характеристики коэффици-

ента прохождения W (0) нулевой моды (q = 0) области I при разных уг- лах изгиба. Характерные размеры областей I и II полагались одинако- выми, т.е. h1 = h2 = h. Как видим, для углов изгиба θ ≤ 90° наблюдает- ся уменьшение коэффициента прохождения с увеличением угла изги- ба θ, что является физически понятным результатом.

При величине h λ, независимо от угла изгиба волновода θ, ко- эффициент прохождения W (0) равен единице, что соответствует рас- пространению звука в очень узкой трубе: “волна бежит в такой трубе, не замечая изгибов, так же, как если бы труба была вытянута в пря- мую линию” [20, с. 168]. Обращает на себя внимание наличие прова- лов в характеристиках, когда h кратно λ2 , а при угле θ = 90° в этих

случаях получаем нулевые значения коэффициента прохождения W (0). При hλ = 0,5 для всех углов изгиба имеем W (0) = 0.

Чтобы понять характер кривых на рис. 10.8 рассмотрим рис. 10.9, где приведены частотные зависимости коэффициентов возбуждения

мод Wn(0) области II при падении на изгиб в области I нулевой моды

634

(q = 0). Напомним, что нулевая мода в однородном волноводе с жест- кими границами распространяется при любом волновом размере вол- новода, в то время как мода с номером n > 0 согласно (10.66) являет- ся распространяющейся только при выполнении условия k > nπh2

или h2 > nπk = nλ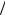2 . На рис. 10.9, а представлены кривые, соответ-

ствующие изгибу под углом θ = 65°, на рис. 10.9, б — θ = 90° при h1 = =h2 = h. Если волновой размер h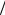λ < 0,5 , то в области II распростра-

няется только нулевая мода (кривая n = 0 ), и она определяет прохож- дение нулевой моды области I через изгиб. Ситуация изменяется, если h/λ > 0,5. Это наглядно иллюстрирует рис. 10.8. Так, при угле изгиба θ = 65° (рис. 10.9, а) при h/λ > 0,5 возбуждается однородная первая мода (кривая n = 1), которая по энергии значительно превосходит ну- левую, а при h/λ > 1 доминирует вторая мода (кривая n = 2), и далее с увеличением h/λ доминируют поочередно моды с высшими номера- ми.

Рис. 10.9. Частотные зависимости энергетических коэффициентов возбуж- дения мод области ΙΙ Wn(0) при h1 = h2 = h :

а — θ = 65°; б — θ = 90°

Таким образом, можно говорить о трансформации энергии нуле- вой моды области I в моды области II с номерами n ≥ 0 . Анализируя графики на рис. 10.8 (здесь θ ≤ 90°), следует отметить уменьшение эффективности возбуждения мод области II, когда h кратно λ/2, а следовательно, — и уменьшение коэффициента прохождения нулевой моды области I через изгиб (рис. 10.8). Если θ = 90° (рис. 10.9, б), то при величине h кратной λ/2, коэффициенты возбуждения мод (а от- сюда и коэффициент прохождения) равны нулю, т.е. наблюдается эффект “запирания” волновода.

635

Подобная ситуация имеет место в волноводе при неравных, но кратных, размерах h1 и h2. На рис. 10.10 показаны частотные зави- симости коэффициентов возбуждения Wn(0) нормальных волн области II при h2 = h1/2, угол изгиба θ = 90°. При условии h1, h2 λ получен-

ный результат хорошо совпадает с теорией одномодового волновода, для которого энергетический коэффициент прохождения нулевой мо-

ды равен (см. задачу 10.1) [41, с. 157—160]:

Так, при h2/h1 = 0,5 согласно формуле (10.75) имеем W (0) ≈ 0,89 , что совпадает с графическими данными на рис. 10.10.

Рис. 10.10. Частотные зависимости Рис. 10.11. Частотные зависимости энергетических коэффициентов воз- энергетических коэффициентов воз-

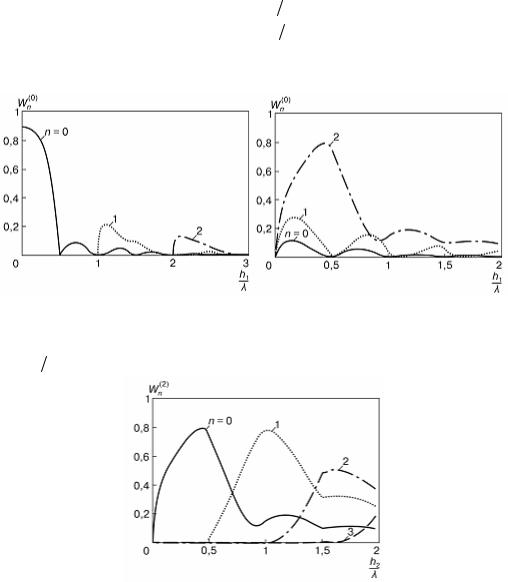
Рис. 10.12. Частотные зависимости энергетических коэффициентов возму- щения мод области II Wn(2) при h1/λ =1,2 , θ = 90°

636

Анализ приведенных выше графиков для волноводов с кратными величинами h1 и h2 позволяет сделать интересный вывод: снижение (а для угла изгиба θ = 90° “запирание” волновода) связано с моментом зарождения очередной моды волновода. Если характерные размеры волновода не кратны λ/2 , то ситуация изменяется. На рис. 10.11

представлены частотные зависимости величин Wn(0) как функции

h1/λ при фиксированном размере h2/λ = 1,2, θ = 90°, q = 0. Величина h2/λ = 1,2 позволяет существовать трем однородным модам области II. Как следствие, частотная зависимость коэффициент прохождения

W (0) нулевой моды через изгиб не будет содержать в себе нулей.

На рис. 10.12 представлены частотные зависимости коэффициен- тов Wn(2) при падении на изгиб второй моды области I(q = 2) . Здесь

размер h1/λ = 1,2 оставался постоянным, а изменялся волновой раз- мер области II h2/λ; угол изгиба θ = 90°. Как видим, когда величина h2 была недостаточна для возникновения однородной второй моды, то вторая мода области Ι трансформировалась в нулевую, потом в первую и далее, с ростом величин h2/λ в звуковое поле распространяющихся нормальных волн. Таким образом, возможна трансформация энергии от высшей моды в низшую моду.

Рис. 10.13. Частотные зависимости энергетического коэффициента проник- новения W(0) при h1 = h2 = h:

1 — θ0 = 125°; 2 — θ0 = 145°

Для волноводов с углом изгиба θ > 90° частотная зависимость ко- эффициента прохождения W (0) иная, чем для углов θ ≤ 90°. Напри-

637

мер, на рис. 10.13 показаны такие характеристики для угла θ = 125° (кривая 1) и θ = 145° (кривая 2) при h1 = h2 = h. Можно указать две особенности в частотной характеристике W (0). Первая особенность на- блюдается при h/λ < 0,5, когда распространяется только нулевая мода, тогда имеем глубокие “провалы” кривых, и звук почти не проникает сквозь изгиб; вторая — при h/λ > 0,5, когда изгиб волновода становит- ся практически звукопроницаемым, что естественно определяется су- перпозицией возбужденных мод с номерами n > 0.

В завершении анализа численных расчетов, можно сказать, что с помощью волновода с изгибом можно эффективно изменять структу- ру звукового поля. Возможна трансформация энергии низшей моды в высшую моду, и наоборот. Очевидно, что волновод с изгибом — это наиболее простое устройство, позволяющее проделать такое преобра- зование энергии с высокой эффективностью. Примером практиче- ского применения есть трансформация энергии нулевой моды в более высокие моды, позволяющая создать условия эффективного ослабле- ния звука в волноводе с поглощающими границами (см. параграф 5.14). Другим практическим применением эффекта трансформации является возможность изменения характеристики направленности излучения из открытого конца волновода с изгибом. (Попробуйте объ- яснить физический механизм в этих двух примерах.)

10.6.2. Распространение звука в волноводе с ответвлением

На рис. 10.14 представлен плоскопараллельный волновод, который имеет вертикальное ответвление. Угол между ответвлением и волноводом составляет 90°. Характерные размеры волновода с от- ветвлением определяются величинами h1 и h2, соответственно Грани- цы волновода — акустически жесткие. Введем систему координат xOy и разделим все пространство волновода на четыре области

(рис. 10.14).

Рис. 10.14. Пример волновода с ответвлением

Пусть слева на зону ответвления падает одна из мод области I в виде (10.62). Предлагаем самостоятельно записать поля давления в выделенных частичных областях и построить решение задачи о рас-

638

пространении звуковой волны в волноводе с ответвлением. Получен- ное решение позволит определить энергетические коэффициенты от- ражения V (q) (формула (10.74)), прохождения в область II основного волновода:

и прохождения в ответвление (область III):

В формулах (10.76), (10.77) величины N2 и N3 определяют количе- ство однородных мод в областях II и III, а Bn и Cn — соответствую- щие амплитудные коэффициенты. Согласно закону сохранения энер-

гии имеем следующее равенство: V (q ) +W (q ) + Wy(q ) =1.

Рассмотрим некоторые численные расчеты, которые иллюстрируют особенности распространения звука в волноводе с ответвлением. На рис. 10.15 представлены частотные характеристики коэффициентов

W (0) (кривая 1) и Wy(0) (кривая 2) как функции волнового размера h1/λ

для двух вариантов: h2 = h1/2 (рис. 10.15, а) и h2 = h1 (рис. 10.15, б).

Рис. 10.15. Частотные зависимости энергетических коэффициентов прохо- ждения W (0) (кривая 1) и Wy(0) (кривая 2):

а −h2 = h12; б −h2 = h1

рис. 10.15 совпадают с результатами теории одномодового волново-

639

да. Согласно этой теории для энергетических коэффициентов прохо- ждения имеем следующие формулы (см. задачу 10.4) [41, с. 171, 178]:

Вычисляя по формулам (10.78), получаем следующие результаты: при h2 = = h1/2 W (0) = 0,64, Wy(0) = 0,32; при h2 = h1 W (0) =Wy(0) ≈ 0,44. Сравнивая

эти данные с графиками на рис. 10.15, отмечаем хорошее совпадение ре- зультатов.

Рис. 10.16. Частотные зависимости энергетических коэффициентов возбу- ждения мод (h1 = h2):

а — в области II; б — в области III

Анализ графиков на рис. 10.15 позволяет следующий сделать вы- вод: с увеличением частоты нулевой моды области I, падающей на зо- ну ответвления, наблюдается рост коэффициента W (0) и уменьшение Wу(0). Отметим, что при h2 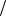λ ≤ 0,5 в случае, когда h1 кратно λ/2, ну-

левая мода в ответвление не проникает (оно “закрыто”), а полностью, без отражения, проходит в область II. Ситуация изменяется, если h2/λ > 0,5. Очевидно, как и для волновода с изгибом, это связано с зарождением мод области III с номерами n > 0. В качестве иллюстра- ции на рис. 10.16 представлена модовая структура поля области II (рис. 10.16, а) и области III (рис. 10.16, б) при h1 = h2. Как видим, в области II доминирует нулевая мода (n = 0 ), а в ответвлении при h2 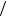λ > 0,5 доминирует первая мода, а при h2 λ >1 — вторая мода об-

ласти III. Таким образом, наблюдается трансформация энергии нуле- вой моды области I в более высокие моды области III. Модовая струк- тура области II определяется плоской волной (n = 0).

640