Основы_акустики_Гринченко_Вовк

Наконец при μ >> 1 (рис. 11.15, в) на графике временной зависимо- сти можно четко выделить участки быстрого и медленного изменения величины х2 = dξ/dτ. Такие колебания называются релаксационными, т.е. связанными с релаксацией (от латинского слова relaxatio — уменьшение, ослабление). Здесь время выхода фазовой точки на пре- дельный цикл очень мало. При μ >> 1 время релаксации системы (т.е. временной отрезок медленного изменения величины x2 ), а, следова-

тельно, и период автоколебаний полностью определяется значением параметра μ. Вследствие этого и возникло само понятие ”релаксаци- онные автоколебания”. Системы с релаксационными автоколебания- ми характеризуются существенной нелинейностью и значительным обменом энергии с источником.

Графики на рис. 11.15 позволяют сделать следующие общие выво- ды: если в автоколебательной системе потери энергии на трение малы по сравнению с энергией колебательного движения, то и энергия, не- обходимая для компенсации потерь, также мала (для уравнения (11.101) это соответствует малому значению параметра μ). Поступая в систему малыми порциями, энергия компенсирует потери энергии, которые возникают при колебаниях, но при этом очень мало изменя- ется сам процесс колебаний. Автоколебания по форме близки к гар- моническим, и их период почти совпадает с периодом собственных колебаний системы. Если потери на трение значительные, а значит, и велика энергия, которая поступает от источника, то автоколебания могут по форме значительно отличаться от гармонических, и их пе- риод может существенно отличаться от периода собственных колеба- ний. Поэтому, например, маятник хороших часов, у которых потери на трение малы, выполняет колебания, которые по форме почти не отличаются от гармонических, а их частота почти точно совпадает с частотой собственных колебаний маятника, (это обеспечивает точ- ность хода часов).

11.11.3. Почему звучит скрипка

Звучание скрипки обусловлено движением смычка. Понят- но, что нельзя объяснить все сложные явления, связанные с особенно- стями звучания скрипки. Однако попробуем в принципе разобраться, почему возникают колебания струны скрипки, когда по ней проводят смычком [*].

Сила трения между смычком и струной — это сила сухого трения. Природа этой силы уже изучалась, и на рис. 11.14, б приведена ее типичная характеристика со спадающим и восходящим участками.

* Асламазов Л.Г., Варламов А.А. Удивительная физика. — М.: Наука, 1987. — С. 48—53.

751

Итак, пусть смычок двигается с постоянной скоростью v0, а струна отклонена от положения равновесия таким образом, чтобы равнодей- ствующая сил упругости уравновесила силу трения скольжения Fт (v0). Если струна случайно отклонится в сторону движения смычка, то от- носительная скорость υ = υ0 − x ( x — скорость струны) уменьшится.

Если относительная скорость смычка и струны при колебаниях стру- ны находится в пределах спадающего участка зависимости силы тре- ния от скорости (рис. 11.14, б), то, как следствие, сила трения возрас- тет и струна отклонится еще больше. При дальнейшем отклонении упругая сила в некоторый момент обязательно превысит силу трения, ведь сила трения скольжения не может быть больше, чем максималь- ное значение силы трения покоя Fт max, и струна начнет двигаться в противоположную сторону. Она пройдет положение равновесия, сно- ва отклонится, остановится и т.д.: таким образом, будут возбуждать- ся колебания струны.

Важно, что эти колебания будут незатухающие. Действительно, при движении струны в направлении движения смычка сила трения скольжения выполняет положительную работу, а в противоположном направлении — отрицательную. Но скорость скольжения υ0 − x в

первом случае меньше, чем скорость υ0 + x во втором, а сила трения Fт(υ0 − x), наоборот, больше, чем Fт(υ0 + x) . Таким образом, положи-

тельная работа сил трения при движении струны в направлении движения смычка больше, чем отрицательная работа при противопо- ложном движении струны, и в целом сила трения выполняет положи- тельную работу. Амплитуда колебаний будет увеличиваться, но до оп- ределенной величины. Когда скорость скольжения выходит за преде- лы спадающего участка, отрицательная работа силы трения может стать больше положительной. Энергия, а, следовательно, и амплитуда колебаний будут уменьшаться.

Таким образом, струна будет колебаться с амплитудой, при кото- рой полная работа сил трения равна нулю. Здесь следует отметить, что часть положительной работы компенсирует затраты энергии на возбуждение колебаний корпуса скрипки, к которому прикреплены струны. Сами колебания корпуса скрипки возбуждают звуковые вол- ны в окружающей среде, ведь струна является очень неэффективным источником звука (см. п. 7.12.1). Итак, часть положительной работы силы трения скольжения тратится на создание звуковой энергии, ко- торую излучает скрипка. С такой постоянной амплитудой и будут происходить незатухающие колебания струны.

Возникновение звуковых колебаний при движении одного твердо- го тела по поверхности другого происходит достаточно часто: сухое трение в дверных завесах может вызвать их скрип; скрипят полови- цы, обувь; скрип можно вызвать, если просто пальцем провести по

752

любой гладкой поверхности. Явления, которые здесь возникают, ана- логичны возбуждению колебаний струны скрипки. Вначале скольже- ния нет, и возникает упругая деформация. Дальше происходит от- рыв, и возбуждаются колебания тела. Колебания не затухают, по- скольку благодаря спадающей характеристике сил сухого трения по- ступает необходимая энергия за счет работы этих сил.

При изменении характера зависимости сил трения от скорости скрип пропадает. Известно, например, что для этого достаточно сма- зать скользящие поверхности. В случае, когда сила вязкого трения пропорциональна скорости, условий, необходимых для возбуждения колебаний, нет. Наоборот, если необходимо вызвать колебания, по- верхности специально обрабатывают, чтобы достичь более резкого уменьшения сил трения при увеличении скорости. Например, для этого смычок скрипки натирают канифолью.

11.12. Вынужденные колебания нелинейного осциллятора

Как нам известно, вынужденными называют колебания, которые возникают и поддерживаются за счет внешнего воздействия на систему, не имеющую других источников энергии. Можно выде- лить два способа внешнего воздействия: первый из них - это непо- средственное силовое влияние на систему, второй - параметрическое влияние, когда внешняя сила заставляет периодически изменяться некоторый параметр колебательной системы (например, длину нити маятника). Второй способ внешнего воздействия рассмотрим в пара- графе 11.14, а сейчас сосредоточим свое внимание на первом.

Влинейных системах с внешним воздействием отклик системы представляют собой сумму собственных и вынужденных колебаний. С течением времени собственные колебания затухают и в системе ос- таются чисто вынужденные колебания или, как говорят иначе, в сис- теме присутствует стационарный режим колебаний.

Внелинейных системах с внешним воздействием суперпозиции собственных и вынужденных колебаний не существует. Поэтому в та- ких системах вынужденные колебания нужно определять как стацио-

нарные процессы (время t → ∞), когда про начальные условия система ”забыла”. Понятно, что для этого система должна быть диссипатив- ной. Итак, будем считать, что в системе присутствует диссипация энергии, а время наблюдения достаточно велико, чтобы обеспечить независимый от начальных условий режим вынужденных колебаний.

753

в отклике взаимосвязаны, так что ни одна из них не может изменять- ся, не влияя на другие. Чтобы этот утверждение выглядело более на- глядно, устремим в (11.110) и (11.113) добротность Q → ∞, т.е. сдела- ем переход к консервативной системе. Понятно, что такой шаг явля- ется “условным”, ведь вынужденные колебания консервативной сис- темы определяются природой собственных и чисто вынужденных ко- лебаний, однако в нелинейной системе принцип суперпозиции не справедлив. Можно также считать, что диссипация очень мала, но время наблюдения велико, и потому собственные колебания в систе- ме затухли. Итак, при таких условиях с учетом тождества (11.111) формула (11.113) приобретает вид (считаем ϕ = 0):

где An (ξ1,ξ3,ξ5,...) — коэффициенты при cos(nγτ) . Для выполнения ра- венства (11.114) необходимо, чтобы

Система (11.115) наглядно иллюстрирует взаимосвязь гармонических составляющих отклика осциллятора. Рекомендуем читателю, оставив

Система уравнений (11.116), (11.117) иллюстрирует в явном виде взаимосвязь между первой и третьей гармониками.

Рассмотрим диссипативный осциллятор. За генерацию высших гармоник с частотами nγ, n = 1,3,5..., отвечает член εξ3 в уравнении (11.110). Поскольку величина ε << 1 и, как мы полагаем, частота внешнего воздействия ω близка к собственной частоте осциллятора ω 0, то можно записать приближенное уравнение для амплитуды пер- вой гармоники ξ1. Для этого, учитывая (11.111), оставляем в (11.113) только члены с n = 1:

756

Перепишем это выражение в таком виде:

если C = cos ϕ и D = sinϕ, ведь cos ϕcos(γτ − ϕ) − sinϕsin(γτ − ϕ) = cos(γτ).

Отсюда величины C и D связаны соотношениям C 2 + D 2 = 1. Подста- вив в уравнение C 2 + D 2 = 1 выражения для C и D, найдем связь ме- жду амплитудой первой гармоники ξ1 и нормированной частотой внешнего воздействия γ = ω /ω 0:

а также соотношение, которое определяет сдвиг фазы между внеш- ней силой и откликом системы:

Определим зависимость амплитуды ξ1 от частоты внешнего воз- действия γ. Сначала, чтобы облегчить анализ, устремим Q → ∞ (это соответствует системе без демпфирования). Тогда перепишем

(11.120) в виде

Уравнение (11.121) можно получить из (11.116), положив |ξ3| << |ξ1|, что действительно справедливо в диапазоне частот вблизи ω0. Еще раз подчеркнем, что решение уравнения (11.121) имеет “условный” характер, ведь его следует рассматривать как частное решение неод- нородного уравнения. Получить общее решение, прибавив к частному общее решение соответствующего однородного уравнения, нет воз- можности, поскольку принцип суперпозиции не работает. Однако ха- рактер влияния демпфирования на резонансную кривую осциллятора по сравнению с консервативной системой для нас уже понятен. По- этому, исследовав достаточно простое уравнение (11.121), мы выяс- ним поведение кривой, которая определяется уравнением (11.120).

На рис. 11.16, а представлена зависимость амплитуды ξ1 (кривая 1) от частоты γ 2 для системы с жесткой нелинейностью (знак плюс в уравнении (11.121)) при ε = 0,1. Данная кривая является результатом

757

сложения параболы 1+ (34)εξ12 (кривая 2) и гиперболы — 1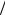ξ1 (кривая

3). Как и в случае линейного осциллятора (рис. 2.10) кривая отклика на внешнее воздействие имеет две ветви: в одной смещение находит- ся в фазе, а в другой — в противофазе с внешней силой. Обе ветви

асимптотически приближаются к кривой 1+ (3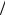4)εξ12 . Понятно, что полуплоскость γ2 < 0 не имеет физического смысла.

Рис. 11.16. Резонансные кривые консервативного осциллятора (ε = 0,1):

а, б — жесткая нелинейность; в — мягкая нелинейность; г — линейный ос- циллятор (ε = 0)

На рис. 11.16, б представлены зависимости модуля |ξ1| от γ2 для системы с жесткой нелинейностью (ε = 0,1), на рис. 11.16, в — для системы с мягкой нелинейностью (знак минус в уравнении (11.121)). Рис. 11.16, г соответствует линейной системе (ε = 0). Интересно отме-

тить, что парабола γ2 =1± (34)εξ12 (для линейной системы на рис.

758

11.16, г она преобразуется в прямую линию) определяет связь между частотой и амплитудой свободных колебаний консервативного нели-

нейного осциллятора. При этом выражение γ = 1± (34)εξ12 ≈1± (38)εξ12

совпадает с формулой (11.70) для частоты свободных колебаний ос- циллятора с кубической нелинейностью, которая получена асимпто-

тическим методом. Линию γ2 =1± (34)εξ12 называют скелетной кри-

вой.

Приведенные графики позволяют отметить следующие особенно- сти колебаний нелинейной системы:

1)отсутствие бесконечного роста амплитуды ξ1 как при совпаде- нии ω с ω 0, так и при ω ≠ ω 0, что обусловлено зависимостью периода колебаний нелинейной системы от ее амплитуды;

2)неоднозначность процесса колебаний в зависимости от направ-

ления изменения частоты внешней силы ω. Это связано с неодно- значностью зависимости ξ1 от γ 2 для ряда частот. Для системы с же- сткой нелинейностью эти частоты находятся выше, а для системы с мягкой нелинейностью — ниже частоты линейного резонанса ω 0. Понятно, что наклон резонансной кривой на рис. 11.16, б, в зависит от значений параметра ε: чем значение ε больше, тем сильнее накло- няется резонансная кривая вправо или влево, соответственно. При

ε= 0 (линейная система, рис. 11.16, г) наклон отсутствует;

3)параметр ε = (хст/d 2), но хст = F0/K; отсюда следует, что пара-

метр нелинейности зависит от амплитуды F0 внешней силы, этот

вывод очень важен.

Вернемся к нелинейному диссипативному осциллятору, и в каче- стве примера рассмотрим систему с жесткой нелинейностью. Чтобы детальнее проанализировать уравнение (11.120), преобразуем его к удобной для проведения вычислений форме. Для этого введем сле- дующие обозначения:

зующий внешнее воздействие;

• y = 34 εQξ12 — безразмерный параметр, характеризующий ампли-

туду вынужденных колебаний;

Рис. 11.17. Резонансные кривые нелинейного осциллятора с диссипацией:

1-5 — Р = 0,8; 1,3; 1,77; 2,6; 3,2; Q = 30

Используя разные значения параметра внешнего воздействия Р, строим ряд кривых y = y (P ), которые представляют собой резонанс-

ные кривые нелинейного осциллятора в безразмерных координатах y и (рис. 11.17). Резонансные кривые, которые находятся ниже кри- вой 3, характеризуются однозначной зависимостью амплитуды вы- нужденных колебаний от частоты внешней силы. Резонансные кри- вые такого типа представляют собой несколько деформированные кривые зависимости амплитуды колебаний от частоты для линейного осциллятора с демпфированием. Для системы с жесткой нелинейно- стью их максимумы смещены вправо. Для кривой 3 характерно появ- ление вертикальной касательной. При дальнейшем увеличении ам- плитуды внешнего воздействия резонансные кривые располагаются выше кривой 3, и в них появляются участки с вертикальными каса- тельными, которые определяют область неоднозначной зависимости амплитуды колебаний от частоты внешнего воздействия. Появление этой неоднозначности и связанные с ней явления заслуживают спе- циального обсуждения.

На рис. 11.18 представлено поведение одной резонансной кривой диссипативного осциллятора с жесткой нелинейностью (сравните с рис. 11.16, б). Определим координаты точки M пересечения резо-

нансной кривой со скелетной кривой 1− γ2 + 3εξ12 4 = 0 . Для точки M в соответствии с (11.120) имеем ξ12 = Q2 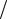γ2 . Подставляя это соотноше- ние в уравнение скелетной кривой 1− γ2 + 3εξ12 4 = 0, получаем урав-

нение для абсциссы точки М : γ4 − γ2 − 3εQ24 = 0 . Отсюда координа- ты точки М имеют следующие значения:

760