Основы_акустики_Гринченко_Вовк

Рис. 10.22. Картина векторного поля интенсивности:

а-в — 2h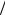λ =1 , θ0= 25°, q = 0, W (0) ≈1; г — 2h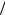λ =1,1, θ0 = 50°, q = 1,

W (1) ≈ 0,84

На рис. 10.22, а-в показан процесс пространственного преобразо- вания потоков энергии в клинообразном волноводе при отдалении от зоны сопряжения и падении нулевой моды (q = 0) в области I. Если в непосредственной близости от зоны сопряжения (рис. 10.22,а) поток энергии сконцентрирован вдоль оси волновода, т.е. практически со- храняется картина потока энергии в плоскопараллельном волноводе, то уже на расстоянии приблизительно 3λ (рис. 10.22, б) модуль ин- тенсивности приобретает почти постоянное значение вдоль сечения

651

волновода. Далее, согласно рис. 10.22, в, с увеличением координаты х поток энергии, уменьшаясь вдоль оси волновода, возрастает вблизи клинообразных границ. При дальнейшем увеличении координаты x пространственное распределение модуля вектора интенсивности асимптотически приближается к зависимости, которая определяется кривой с параметром 2hλ =1 на рис. 10.20, б. Если в области I пада-

ет первая симметричная мода (q = 1), то картина изменяется, и это можно увидеть на рис. 10.22, г. Здесь, как видим, процесс простран- ственной перестройки потоков энергии происходит достаточно быст- ро.

Итак, можно сделать вывод, что энергетическая характеристика направленности определяется совокупностью факторов, а именно: волновым размером плоскопараллельного волновода 2h/λ, углом рас- крыва клинообразного волновода θ0 и структурой падающей волны. Эти данные важны для формирования представлений об особенно- стях излучения звука из клинообразного рупора в открытое про- странство.

10.7. Рассеяние звука на клинообразном объекте

Задача о рассеянии волны на клине представляет собой фундаментальную проблему, на решении которой базируются многие представления о волновых процессах в акустике, оптике и радиофи- зике. Учитывая это, в предыдущем разделе была построена функция Грина для клинообразной области. Особенно интересной является за- дача о рассеянии волн на клинообразном объекте конечных размеров. Анализ поля рассеяния от подобных объектов лежит в основе по- строения систем локации.

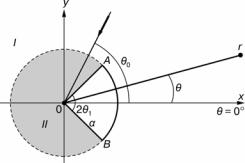
Рис. 10.23. Пример клинообразного объекта

Рассмотрим плоскую задачу рассеяния звука на клинообразном объекте (рис. 10.23), т.е. полагаем, что объект имеет бесконечную про- тяженность вдоль оси, перпендикулярной к плоскости рисунка. Объ-

652

ект представляет собой клин с углом 2θ1, стороны которого замкнуты дугой АВ окружности радиуса а. Поверхности объекта считаем аку- стически жесткими. Клинообразный объект находится в идеальной среде плотностью ρ, со скоростью звука с. Чтобы описать геометрию объекта и построить решение задачи, введем полярную систему ко- ординат rOθ с центром в угловой точке клина.

Согласно идее метода частичных областей все пространство суще- ствования звукового поля естественно делится на две области: I — вне окружности радиуса а, т.е. r ≥ a, 0 ≤ θ ≤ ≤ 2π; II — сектор круга

радиусом а, а именно: 0 ≤ r ≤ a, θ0 ≤ θ ≤ 2π – θ0.

Пусть в области I на клинообразный объект (рис. 10.23) падает

r sinθ } — вектор, определяющий точку наблюдения в звуковом поле. Знак “минус” в показателе экспоненты указывает на то, что направ- ление распространения плоской волны противоположно направлению роста радиальной координаты r (рис. 10.23). Углы θ0 и θ определяют, соответственно, угловое направление падения волны и направление на точку наблюдения. Используя значения проекций векторов k и r на оси декартовой системы координат xOy, перепишем выражение для плоской волны в виде

В дальнейшем нам понадобится представление падающей волны

(10.93) в виде ряда (см. (8.25)):

∞

p0 = ∑ (−i)n εn Jn (kr )cos (n (θ − θ0 )), (10.94)

n =0

где ε0 =1, εn = 2 , если n > 0 , Jn(kr) — функция Бесселя первого рода.

При взаимодействии плоской волны с клинообразным объектом обра- зуется рассеянное поле, которое можно представить в виде суперпози-

ции цилиндрических бегущих волн типа Hn(1) (kr )cos (nθ), n = 0,1,2,... и Hn(1) (kr )sin(nθ), n =1,2,3,... Комбинация угловых функций cos(nθ) и

sin(nθ) необходима, ведь угол падения плоской волны θ0 считается произвольным, поэтому симметрия отсутствует. Итак, поле давления в области I будет иметь вид

653

где числа αn определяются из граничных условий на жестких гра-

Построенные решения для областей I и II действительно общие, т.е. они способны удовлетворить любым условиям на границах частичных областей.

Запишем условия сопряжения на границе раздела частичных об-

ластей I и II (рис. 10.23):

Алгебраизацию функционального уравнения (10.98) проводим благо- даря ортогональности системы функций cos(αn(θ – θ1)), n = 0,1,2,… на отрезке θ = [θ1,(2π – θ1)]. Алгебраизацию функционального уравнения (10.99) проведем дважды : первый раз—используя систему функций cos(nθ), n = 0,1,2,…, второй —используя систему sin(nθ), n = 1,2,3,…

Обе системы функций ортогональны на отрезке θ = [0,2π]. Итак, полу- чим бесконечную систему линейных алгебраических уравнений вто- рого рода относительно неизвестных коэффициентов An, Bn, Cn.

Бесконечная система уравнений решалась методом редукции. Для оценки точности выполнения условий сшивания полей определим от- клонение как отношение модуля разности характеристик поля (давле- ние или колебательная скорость) слева и справа от границы раздела частичных областей к амплитуде плоской падающей волны на клино- образный объект. Например, отклонение по давлению определяется

по такой формуле: δр = |pI – pII| / |p0|.

Проведем анализ отклонения для данной задачи, поскольку, кроме сугубо численных величин, здесь можно проследить интересные мо- менты. Пусть имеем клинообразный объект с ka = 15, θ1 = 45°. Угол па- дения плоской волны θ0 = 90°. Волновой размер объекта достаточно большой, поэтому при счете удерживалось по 40 коэффициентов An,

654

Bn, Cn, соответственно. На рис. 10.24 представлены графики отклоне- ния по давлению δр (сплошная кривая) и по колебательной скорости δυ (штриховая) вдоль окружности радиуса а (r = a). Диапазон углов θ = [0,θ1] и θ = [(2π -θ1),2π] соответствует жесткой поверхности объекта (рис. 10.23), поэтому в этом диапазоне углов определялись относитель-

ные величины δp = |pI| / |p0|, δυ = |υrI| / |υr0|.

Рис. 10.24. Кривые отклонения по давлению δр (сплошная кривая) и по ко- лебательной скорости δυ (штриховая) вдоль окружности радиуса r = a

(рис. 10.23); ka = 15°, θ1 = 45°, θ0 = 90°

Следует отметить резкий рост отклонения δυ в окрестности ребра клинообразного объекта θ = ± θ1 = ±45°, r = a. Как мы знаем, в рамках используемой модели такой результат целиком предсказуем. При ус- ловии ka = 15, θ1 = 45° жесткие границы объекта имеют значитель- ные волновые размеры. Поэтому амплитуда давления на этой по- верхности приблизительно равна удвоенной амплитуде падающей волны. Этот факт находит свое отражение на рис. 10.24 для углов θ = 0—45°, θ = 315—360°. В целом, если отклонение δ < 0,1, то можно считать выполнение граничных условий на границе раздела частич-

Это обусловлено тем, что ограничение количества уравнений в беско- нечной системе вносит погрешность при выполнении граничных усло- вий именно по высоким гармоникам в соответствующих рядах Фурье.

При решении задачи о рассеянии звука препятствием (см. раздел 8), обычно, исследуют звуковое поле в дальней зоне. Здесь рассеянное поле представляет собой сферическую расходящуюся волну. Для пло- ской задачи, которую мы сейчас исследуем, это соответствует цилин-

655

дрической расходящейся волне. Согласно (10.95) комплексная ампли- туда рассеянной волны имеет вид

С учетом асимптотик функций Ханкеля при kr → ∞ (см. 10.88) форму- лу (10.100) можно записать так:

Интенсивность в дальнем поле рассеянной волны определяется из- вестным соотношением Irs =| ps |2 (2ρc ). Тогда, согласно (10.101) име- ем

где I0 =1(2ρc )— интенсивность падающей плоской волны единичной амплитуды (10.93), “*” — знак комплексного сопряжения, а

∞

L (θ,θ0 ) = A0 + ∑ exp(−inπ2)(An cos (nθ)+ Bn sin(nθ)). (10.103)

n =1

Мощность рассеянной волны при интегрировании (10.103) по окруж- ности радиуса r определится соотношением:

Подставляя (10.103) в (10.105), получаем следующую формулу для безразмерной величины σs :

Согласно определению (8.8) позиционное сечение рассеяния σ (θ, θ0 ) = = 2πrIrs(θ, θ0) / I0. Подставляя в это определение выражение (10.102),

656

получаем соотношение для безразмерной величины позиционного се- чения рассеяния:

Если в формуле (10.107) положить угол θ = θ0, то получим сечение об-

ратного рассеяния σL (θ0 ) = σ (θ = θ, θ0).

Перейдем к анализу численных расчетов. На рис. 10.25, а пред- ставлены величины сечения рассеяния σs, σ, σL как функций угла па- дения плоской волны θ0 на клинообразный объект, для которого ka = 15 (или а ≈ 2,4λ), θ1 = 45°. При таких параметрах объект имеет значительные волновые размеры, причем дуга АВ и грани клина ОА, ОВ приблизительно одинаковы по волновым размерам.

Рис. 10.25. Зависимость сечения рассеяния от угла падения плоской волны θ0; кривая 1 — σs /a, кривая 2 — σ (θ = 0, θ°)/a, кривая 3 — σL /a:

a — ka = 15, θ1 = 45°, б — ka = 0,7, θ1 = 45°, в — ka = 15, θ1 = 3°

657

Как видим, полное сечение рассеяния σs (кривая 1) практически не зависит от угла падения волны θ0, что обусловлено заданными размерами объекта. Позиционное сечение рассеяния σ (θ = 0, θ0) (кри- вая 2) характеризует энергию рассеянной волны в направлении θ = 0 как функцию угла падения плоской волны θ0. Наблюдается наличие “теневого” лепестка (угол падения θ0 = 180°). Особый интерес пред- ставляет сечение обратного рассеяния σL (кривая 3). При углах паде- ния θ ≈ 0—70° кривая 3 является плавной, что соответствует отраже- нию волны от поверхности AB (рис. 10.23) значительного волнового размера (длина дуги AB составляет приблизительно 3,75λ). Диапазон углов θ ≈ 70—180° можно охарактеризовать как отражение волны от плоского участка OA поверхности клинообразного объекта. Здесь на- блюдается значительная “изрезанность” кривой 3. При угле падения θ ≈ 135° имеем так называемый блик, т.е. резкое увеличение ампли- туды отраженной волны в противоположном направлении, обусловле- но нормальным падением плоской волны на границу ОА большого волнового размера.

Если резко уменьшать волновой размер объекта, скажем, ka = 0,7; θ1 = 45°, как на рис. 10.25, б, то, соответственно, уменьшатся величи- ны сечений рассеяния σs, σ, σL и три кривые становятся плавными.

На рис. 10.25, в имеем графики для объекта с большим значением ka = 15, но малым углом θ1 = 3°. Понятно, что геометрия объекта из- менилась. Здесь волновая длина дуги АВ приблизительно в десять раз меньше величины ka и составляет 0,24λ. Отсюда становится понят- ным ход кривой 1 для полного сечения рассеяния, которая резко спа- дает в окрестности углов θ0 = 0°, 180°. По сравнению с рис. 10.25, а значительно уменьшилось позиционное сечение рассеяния σ (θ = 0, θ0) (кривая 2). Величина сечения обратного рассеяния σL (кривая 3) имеет ярко выраженный характерный максимум в окрестности угла паде-

ния θ0 = 90°.

Итак, можем сделать вывод о том, что сечение рассеяния объекта, а, следовательно, и возможность его локации, существенно зависят от геометрии объекта, волновых размеров поверхностей, которые его образуют, и направления падения волны.

10.8. Излучение звука диском

Задача об излучении звука круглым диском занимает осо- бое место в акустике. Указать время, когда она впервые была сфор- мулирована, сейчас вряд ли возможно. Однако можно сказать, что уже во времена Рэлея она вызывала несомненный интерес, и сам Рэ- лей уделил ей большое внимание [50].

658

Может возникнуть вопрос – почему на протяжении уже более 150 лет эта задача продолжает оставаться актуальной? Причина этого, как нам представляется, обусловлена двумя обстоятельствами. Во- первых, потребностями практики. Действительно, во многих практи- ческих ситуациях поле, создаваемое колеблющимися элементами аку- стических приборов, зачастую вполне удовлетворительно может быть представлено, как поле круглого колеблющегося диска. К таким эле- ментам следует отнести диффузоры, широко используемых в воздуш- ной акустике электродинамических и электростатических громкого- ворителей, стержневые и пластинчатые пьезокерамические преобра- зователи. Кроме этого, данные о поле излучения диска часто исполь- зуются для оценок полей, создаваемых вибрирующими поверхностя- ми различных строительных конструкций, машин и механизмов.

Вторая причина кроется в том, что задача об излучении круглого диска обладает большой физической и математической содержатель- ностью, а изучение ближнего и дальнего полей излучения диска весь- ма поучительно и позволяет продемонстрировать интересные особен- ности такого сложного волнового процесса, как дифракция звука. Кроме этого, такой объект, как круглый диск, имеет сравнительно простую геометрию и поэтому задача об излучении звука диском не- редко используется как тестовая при сравнении эффективности раз- личных методов ее решения.

Вдевятом разделе, на базе интегральных соотношений исследова- лось звуковое поле диска, помещенного в акустически жесткий эк- ран. Однако, как было отмечено, анализ ближнего поля на базе инте- гральных методов является непростой вычислительной задачей.

Вданном параграфе покажем, как на базе метода частичных об- ластей можно с единых методических позиций находить решения большого класса задач, где главным элементом является колеблющий- ся поршень или диск, “встроенный” в различные по форме и акусти- ческим свойствам экраны. При этом никаких ограничений на харак- тер распределения колебательной скорости по поверхности диска не накладывается.

10.8.1. Диск в бесконечном экране

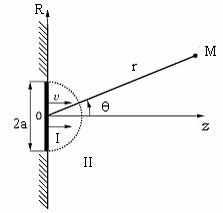
Пусть имеем бесконечный акустически жесткий или мяг- кий плоский экран (рис. 10.26), в котором расположен круглый диск радиуса а. Экран перпендикулярен к плоскости рисунка. Диск колеб- лется по гармоническому закону с частотой ω и амплитудой колеба- тельной скорости υz (S ) = υ0 , т. е. скорость на поверхности S диска

распределена равномерно. В такой ситуации диск называют порш- нем. Поскольку экран бесконечный, то звуковые волны, которые об-

659

разуются слева и справа от экрана, не взаимодействуют между со- бой. Рассмотрим полупространство справа от экрана.

Рис. 10.26. Пример диска в плоском экране

Введем сферическую систему координат (рис. 10.26) с центром в точке О, которая совпадает с центром диска. Положение точки про- странства определяется расстоянием r и углами θ и ψ. Угол ψ рассчи- тывается на плоскости z = 0, совпадающей с плоскостью экрана. По- скольку скорость колебаний всех точек диска одинаковая, т. е. имеет место осевая симметрия относительно оси Oz, то характеристики зву- кового поля не зависят от угла ψ. Согласно методу частичных облас- тей разделим полупространство на две области:

1) 0 ≤ r ≤ a, 0 ≤ θ ≤ π/2; 2) a ≤ r < ∞, 0 ≤ θ ≤ π/2.

Построим общее решение уравнения Гельмгольца для каждой из областей. Начнем с области II. Вернемся к седьмому разделу п. 7.12.2, где рассматривался сферический излучатель в свободном простран- стве. В случае, когда колебательная скорость поверхности сферы не зависит от угла ψ (т.е. V (θ, ψ) ≡ V(θ)), звуковое поле сферы представля- ется в виде суперпозиции (см. (7.195)) сферических волн типа

ции Ханкеля первого рода, Pm (cos θ) — полиномы Лежандра. Теперь

обратимся к рис. 10.26. Граница раздела областей I и II в виде полу- сферической поверхности может считаться источником, который создает звуковое поле в области II. Поэтому, можно утверждать, что полусферическая поверхность r = a, 0 ≤ θ ≤ π/2, 0 ≤ ψ ≤ 2π излучает в

область II бегущие волны с полусферическими фронтами. В сфериче- ских волнах (7.195) порядок функций hm(1) (kr ) и Pm (cos θ) определяет- ся целым числом m = 0,1,2,..., что обусловлено расположением сферы

660