Основы_акустики_Гринченко_Вовк

имеет вид: U(x) = c0 + (1/2)c2(x – x1)2 + …, где c0 =U (x1), c2 = U″ (x1) > 0.

Тогда в окрестности точки x1 выражение (11.11) можно переписать следующим образом:

На плоскости (x,x ) это уравнение представляет собой совокупность эллипсов (рис. 11.2, а) с центром в точке (x1, 0), размеры которых

типа центр (см. рис. 11.1). На рис. 11.2, а показаны случаи, когда величина E = U0,U1,U2 , здесь U0 = U (x1). Если E = U0 , то фазовая кривая вырождается в точку (x = x1, x = 0 ), которая является со- стоянием равновесия. Для значений E < U(x1) фазовых траекторий не существует, что следует из формулы (11.27) и рис. 11.2, а.

Рис. 11.2. Фазовые траектории в окрестности особой точки типа центр (а) и седло (б)

711

В окрестности локального максимума (на рис. 11.2, б это точка х2) потенциальная функция имеет вид ряда U(x) = c0 – (1/2)c2(x – x2)2 + …, где c2 = –U″ (0) > 0. Для малых отклонений от состояния равновесия x = x2 выражение (11.11) имеет вид

Выражение (11.28) определяет на фазовой плоскости семейство гипербол. Имеем особую точку типа седло. При значении E = U(x2) (на

рис. 11.2, б U0 = U (x2 ) ), гипербола вырождается в две прямые, кото-

рые пересекаются в точке (x2, 0) — это сепаратрисы. Однако факти- чески сепаратрисы в точке седла не пересекаются, поскольку не со- держит в себе точку седла. Система, которая следует вдоль сепарат- рисы, при x → x2 будет иметь согласно (11.28) скорость x → 0 , т.е. ко- лебательная система входит в состояние равновесия и выходит из не- го с бесконечно малой скоростью, а, следовательно, бесконечно долго. Другими словами, система может лишь приближаться или отдаляться от неустойчивого состояния равновесия асимптотически (t → ∞). Дей- ствительно, при начальном состоянии, которое точно соответствовало бы состоянию равновесия, система осталась бы в нем навсегда. При этом любое малое отклонение энергии системы в ту или другую сто- рону изменяет движение системы, поэтому движение реальной сис- темы, соответствующее на фазовой плоскости сепаратрисе, невоз- можно.

Приведенные рассуждения дают возможность не только провести анализ фазовых траекторий вблизи особых точек, но и исследовать на качественном уровне характер движения на всей фазовой плоскости, если потенциальная функция U(x) определена для всех х. Например, на рис. 11.3 построен фазовый портрет динамической системы (11.17) по заданному графику U(x). Отметим особую роль сепаратрис: они разделяют фазовую плоскость на области с качественно различ- ным характером движения системы (на рис. 11.3 сепаратрисам соот- ветствуют значения E = U1 и E = U2). Так, сепаратриса (E = U2) отделя- ет область фазовой плоскости, где отсутствуют замкнутые фазовые траектории, от области, где есть замкнутые фазовые траектории.

Итак, если задана потенциальная функция U(x), то построение фазо- вого портрета можно осуществить в такой последовательности:

1)располагаем координатные оси Ох и Ox фазовой плоскости точно под графиком функции U(x);

2)на оси абсцисс Ox обозначаем особые точки, соответствующие устойчивым состояниям равновесия в локальных минимумах функ- ции U(x) (центры) и неустойчивым — в локальных максимумах (седла);

712

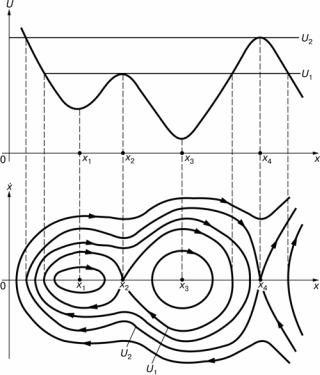
3)проводим на графике функции U(x) горизонтальные касатель- ные в точках максимума; их точки пересечения с кривой U(x) опреде- лят границы раздела областей сепаратрисами соответствующих седел;

4)проводим линии сепаратрис, имеющие в точках седел кривые, которые пересекаются (имеют вид крестика), а также совокупность замкнутых, вложенных одна в одну овальных кривых вокруг центров;

5)стрелки, которые обозначают направление движения вдоль фа- зовых траекторий, расставляем таким образом, чтобы в верхней по-

луплоскости они были направлены право, а в нижней — влево, ведь x > 0 соответствует увеличению координаты х во времени, а x < 0 —

уменьшению.

Рис. 11.3. Построение фазового портрета динамической системы

11.6.2. Диссипативная система

Модель нелинейного осциллятора с демпфированием опи- сывается уравнением x + 2δx + f(x) = 0, где постоянная δ > 0 имеет смысл параметра демпфирования. Такая модель хорошо описывает механические и акустические осцилляторы, когда сила трения про-

713

тора. В общем случае аттракторы могут иметь разную природу (с не- которыми из них мы встретимся ниже). В фазовом пространстве дис- сипативного осциллятора аттрактор представляет собой одну точку — устойчивый фокус или устойчивый узел. Если потенциальная функ- ция U(x) имеет более чем один минимум, то имеем соответственно не- сколько аттракторов, у каждого из которых свой бассейн притяже- ния. При этом сепаратриссы разделяют эти бассейны на фазовой плоскости.

Рис. 11.4. Пример фазовых траекторий линейного осциллятора с демпфиро-

ванием (2.27); начальные условия: x(0) = 0; x (0) = 1; ω0 = 1:

а — δ < ω0, δ1 = 0,085, δ2 = 0,25; б — δ > ω0, δ1 = 1,05, δ2 = 1,75

11.7.Осциллятор с нелинейностью синуса

11.7.1.Аналитический подход

Уравнение осциллятора с нелинейностью в виде функции синуса (2.4) описывает колебание маятника (рис. 2.1, д). Оказывает- ся, что аналогичное уравнение определяет поведение систем и в ряде других физических задачах. Этот факт позволяет рассматривать ос- циллятор с нелинейностью синуса как базовую модель. Кроме того данное нелинейное уравнение дает возможность его аналитического исследования при помощи эллиптических функций Якоби [26, 49].

Такая ситуация при исследовании нелинейного уравнения является достаточно редкой.

Перепишем уравнение (2.4) в виде

Якоби (Jacobi) Карл Густав Якоб (1804—1851) — немецкий математик.

715

седлам на фазовой плоскости. На рис. 11.5, можно выделить три ка- чественно различных типа фазовых траекторий, которым соответст- вует различный характер движения маятника:

1)колебательные движения маятника, в этом случае фазовые тра- ектории замкнуты вокруг особой точки типа центр;

2)движение по сепаратрисам, которые следуют от седла до седлу;

3)вращательные движения.

Рис. 11.5. Фазовый портрет осциллятора (11.30)

Запишем для уравнения (11.30) закон сохранения энергии:

где E = const — полная энергия системы. Колебательным движениям соответствуют значения −1 < Eω02 <1, вращательным — Eω02 >1,

движениям по сепаратриссе — Eω02 =1. Интересным для нас являет-

ся колебательное движение маятника, на нем и сосредоточим свое внимание.

716

Знак плюс соответствует верхней половине фазовой траектории, а минус — нижней. Оставим в дальнейшем в выражении (11.33) верх- ний знак. Введем обозначение m = sin(θ0/2) и новую переменную

где изменение угла θ от 0 к θ0 приводит к изменению ϕ от 0 до π/2. Тогда разделяя переменные в (11.33), получаем дифференциальное уравнение движения маятника:

рирование выполняется по всей замкнутой фазовой траектории, про- интегрируем уравнение (11.35) и найдем период колебаний:

где Т0 = 2π/ω0 — период колебаний линейного маятника. Интеграл

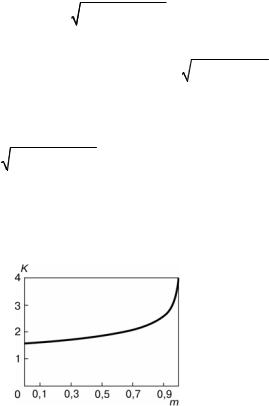
K(m) называют полным эллиптическим интегралом. График функ-

ции K(m) представлен на рис. 11.6. Как следует из рисунка, K(0) = π/2,

lim K (m) = ∞ .

m→1

Рис. 11.6. График функции K(m)

Согласно (11.36) период колебаний маятника зависит от амплиту- ды колебаний, другими словами энергии в системе, поэтому колеба-

ния маятника неизохронные. Если m << 1, т.е. θ0 << π, E /ω02 ≈ −1 , то

T ≈ 2π/ω0, что совпадает с периодом колебаний линейного осциллято- ра. При увеличении энергии колебаний период постепенно возрастает

и при θ0 → π, Eω02 →1, т.е. при приближении траектории на фазовой плоскости к сепаратрисе, стремится к бесконечности.

717

Определим добавку к периоду линейных колебаний Т0, если на- чальный угол отклонения маятника θ0 достаточно мал (m << 1). Тогда

полагая в формуле (11.36) (1−m2 sin2 ϕ)−12 ≈1+ (m2 sin2 ϕ)/2, получаем

приближенную формулу для периода колебаний Т нелинейного осцил- лятора:

Таким образом, при увеличении амплитуды колебаний θ0 период возрастает, причем добавка за счет нелинейности достаточно мала: маятник можно считать изохронным при выполнении условия

θ02 16 <<1. Например, при угле θ0 = 30° относительное изменение пе-

риода равно 0,017, т.е. не более двух процентов.

Теперь определим закон движения маятника. Для этого найдем

Здесь F(ϕ, m) — специальная функция, которую называют неполным эллиптическим интегралом 1-го рода. При 0 ≤ m2 ≤ 1, 0 ≤ ϕ ≤ π/2

функция F является действительной. Очевидно, что F(π/2; m) = K(m). Формула (11.39) устанавливает связь между временем t и откло- нением маятника от положения равновесия, т.е. фактически опреде- ляет закон движения осциллятора. Используя определение эллиптиче- ских функций [26, 49], можно записать точное решение для колеба-

тельного движения маятника:

где sn(ω0t; m) и cn(ω0t; m) — эллиптический синус и эллиптический ко- синус.

На рис. 11.7, а представлены зависимости θ(t) при относительно малой амплитуде колебаний θ0 = 25°, Eω02 ≈ −0,906 , а на рис. 11.7,

б — при большой амплитуде колебаний θ0 = 175°, Eω02 ≈ 0,996 . В

первом случае имеем колебания, близкие к гармоническим, а во вто- ром — существенно нелинейные (или, как говорят иначе, ангармони- ческие) с увеличением периода колебаний. Таким образом, наглядно проявляются основные свойства нелинейных осцилляторов: неизо-

хронность и ангармоничность.

Рис. 11.7. Зависимость координаты θ от нормированного времени:

11.7.2. Асимптотический метод

Случаи, когда удается найти точные решения нелинейных уравнений, достаточно редки. Поэтому в теории колебаний разрабо- тано значительное количество приближенных, или асимптотических, методов [26, 36, 38]. Нашей целью не является их описание, на приме- ре маятника мы лишь познакомимся с некоторыми основными идеями математического и физического характера при таком подходе.

функция синуса sinθ = θ − θ3 /6 + θ5 /120 −... определяет нелинейность

восстанавливающей силы. Рассмотрим случай слабой нелинейности, т.е. будем исследовать относительно малые колебания маятника. По-

719

этому оставим в ряде для функции sinθ первые два члена. Тогда уравнение движения примет вид

При исследовании нелинейных систем широко используется процеду- ра приведения уравнения движения к безразмерному виду; при этом естественно появляются малые параметры. Вообще следует отметить, что условием применения любого асимптотического метода является наличие малого (или большого) параметра. Ниже мы будем приводить такую процедуру, но сейчас этого делать не будем по двум причинам: во-первых, малый параметр в уравнении (11.41) мы уже имеем, а во- вторых, для начала, исследование исходного уравнения движения яв- ляется более наглядным.

Итак, перепишем уравнение (11.41) в виде

где ε = –1/6. Величина ε, которая по модулю меньше единицы, и есть малый параметр. Она определяет отклонение характеристики восста- навливающей силы от линейной зависимости.

Уравнение (11.42) отличается от уравнения гармонического осцил- лятора θ +ω02θ = 0 наличием слагаемого εω02θ3 с малым параметром ε.

Поэтому, вероятно, правильным будет следующий вывод: в действи- тельности решением уравнения (11.42) является несколько откоррек- тированное решение уравнения гармонического осциллятора

θ +ω02θ = 0 . Если это действительно так, то логично искать решение уравнения (11.42) в виде ряда по степеням малого параметра ε:

где θ(0), θ(1), θ(2),... — это так называемые нулевое, первое, второе и другие приближения искомого решения. Понятно, что чем больше членов ряда (11.43) можно определить, тем более точным будет полу- ченное решение. Остановимся на двух членах ряда (11.43), или, как говорят в этом случае, определим нулевое и первое приближения в решении (11.43), т.е.

Подставляем решение (11.44) в уравнение (11.42). При этом в соот- ветствии с намерением получить первое приближение удерживаем в нем члены, которые содержат в себе параметр ε в степени, не выше первой. Как следствие, получаем следующее уравнение:

720