
Обыкновенные дифференциальные уравнения с приложениями к математическим моделям специальных дисциплин. Бырдин А.П., Сидоренко А.А
.pdf
А.П. Бырдин А.А. Сидоренко Л.П. Цуканова
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
СПРИЛОЖЕНИЯМИ
КМАТЕМАТИЧЕСКИМ МОДЕЛЯМ СПЕЦИАЛЬНЫХ ДИСЦИПЛИН
Учебное пособие
|
|
|
|
|
|
divFdV |
FndS |
||||
V |
S |
||||
Воронеж 2012
0
ФГБОУ ВПО “Воронежский государственный технический университет”
А.П. Бырдин А.А. Сидоренко Л.П. Цуканова
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
СПРИЛОЖЕНИЯМИ
КМАТЕМАТИЧЕСКИМ МОДЕЛЯМ СПЕЦИАЛЬНЫХ ДИСЦИПЛИН
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2012
1
УДК 517.2
Бырдин А.П. Обыкновенные дифференциальные уравнения с приложениями к математическим моделям
специальных дисциплин: учеб. |
пособие / |
А.П. Бырдин, |
|||
А.А. Сидоренко, Л.П. Цуканова. Воронеж: |
ФГБОУ |
ВПО |
|||
“Воронежский государственный |
технический |
университет”, |
|||
2012. 255 с. |
|
|
|
|
|
В |
учебном |
пособии |
излагается |
теория |
|
дифференциальных уравнений с приложениями к задачам физики, термодинамики, гидродинамики и экологии. Теоретический материал иллюстрируется большим количеством примеров. Имеются задачи для самостоятельного
решения. |
|
Издание соответствует |
требованиям Федерального |
государственного образовательного стандарта высшего профессионального образования по направлению подготовки бакалавров 140100 «Теплоэнергетика и теплотехника», профиль «Промышленная теплоэнергетика», дисциплине ”Математика”.
Учебное пособие подготовлено в электронном виде в
текстовом редакторе Word 2003 и |
содержится в файле |
ДифУравнения-ПТ.doc. |
|
Ил. 12. Библиогр.: 12 назв. |
|
Научный редактор д-р физ.-мат. |
наук, проф. |
В.Д. Репников
Рецензенты: кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В.А. Костин); канд. физ.-мат. наук, доц. В.Н. Потапов
Бырдин А.П, Сидоренко А.А., Цуканова Л.П., 2012
Оформление. ФГБОУ ВПО “Воронежский государственный технический университет”, 2012
2
ВВЕДЕНИЕ
Настоящее учебное пособие написано авторами на основе лекций, читаемых на протяжении ряда лет во втором и третьем семестрах студентам специальностей “Промышленная теплоэнергетика”, “Радиотехника”, “Роботы и робототехнические системы” Воронежского государственного технического университета. Пособие написано в соответствии с программой курса “Высшая математика” и может быть использовано как студентами специальностей с повышенной математической подготовкой, так и студентами других специальностей.
Учебное пособие содержит также дополнительный материал, рекомендованный студентам для самостоятельного изучения. Содержание этих разделов используется для выполнения курсовых работ по высшей математике, а также для выступлений “продвинутой” части аудитории на семинарских занятиях и в студенческой исследовательской работе. При написании учебного пособия использовались учебники, рекомендуемые в ведущих ВТУЗах России - МЭИ, МИЭТ, МИФИ и др.
Практически во всех разделах пособия приведены приложения вводимых математических понятий к общеобразовательным техническим дисциплинам, изучаемым на младших курсах.
По каждому изучаемому разделу приведены примеры решения задач, а также многочисленные задачи для контроля усвоения материала. Ко всем рекомендуемым для самостоятельного решения задачам приведены ответы. По каждому изучаемому разделу приведены также задачи для самостоятельного решения. Поэтому представленное учебное пособие может быть использовано преподавателями для проведения семинарских занятий.
3
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. ОСНОВНЫЕ ПОНЯТИЯ
1. Понятие обыкновенного дифференциального уравнения, общего и частного решений. Геометрический смысл решения
Многочисленные вопросы науки и техники требуют не только отыскания скорости изменения величин по заданной физической или технической характеристике процесса (т.е. отыскания производных), но и решения обратной задачи – восстановление функции по ее заданной производной. Если
задано, |
например, |
ускорение движения a |
a(t) , то |
||||
восстановить скорость движения v v(t) или |
уравнения |
||||||
движения s |
s(t) можно с помощью интегрирования. Именно, |
||||||
поскольку |
a |
|
dv |
, где |
a(t) - заданная функция времени, то |
||
|
|
||||||
|
|
|
dt |
|
|
|
|
получаем уравнение |
|
|
|
||||
|
|
|
|
|
dv(t) |
a(t) , |
(1.1) |
|
|
|
|
|
|
||
|
|
|
|
|
dt |
||
|
|
|
|
|
|
|
|
из которого определяется скорость движения с точностью до постоянной
v(t) 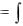 a(t)dt C, (1.2)
a(t)dt C, (1.2)
C - произвольная константа. Неопределенный интеграл в решении (1.2) можно заменить определенным интегралом с переменным верхним пределом.
t
v(t) 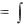 a(t)dt C,
a(t)dt C,
t0
где t0 и t - принадлежат области, в которой задана функция a(t) .
Таким образом, задача отыскания первообразной для функции f (x) , заданной в интервале x (a,b) , приводит к простейшему дифференциальному уравнению
4

y f (x), |
x (a,b) . |
(1.3) |
Если f (x) непрерывная на |
этом интервале |
функция, то |
решение уравнения, как известно из курса математического анализа, дается формулой
|
|
x |
|
|
y |
f (x)dx |
C, |
|
|
x0 |
|
где x0 , x |
(a, b) , C - произвольная постоянная. |
||
Уравнение (1.3) представляет собой наипростейший тип |
|||
Для |
потребностей |
самой |
математики, а также ее |
приложений в естественно - научных и технических дисциплинах, приходится определять функцию y y(x) из более сложных соотношений, связывающих значения
независимой переменной x со |
значениями как |
самой |
неизвестной функции y , так и ее производных y , y ,... : |
|
|
F (x, y, y ,..., y (n) ) |
0, |
(1.3) |
где F (x, y, y ,..., y (n) ) - заданная функция (n 1) - переменных.
Такого рода соотношения называются обыкновенными дифференциальными уравнениями. Термин “обыкновенное” означает, что входящая в уравнение неизвестная функция за висит только от одного независимого переменного x .
Обыкновенным дифференциальным уравнением 1-го порядка называется соотношение, связывающее независимое переменное x , неизвестную функцию этого переменного y(x)
и ее производную 1-го порядка y (x) .
Общий вид уравнения таков:
F(x, y, y ) 0, |
(1.5) |
где F(x, y, y ) - заданная функция.
Решением дифференциального уравнения (1.5) назовем всякую дифференцируемую функцию y 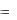 (x) удовлетворяющую этому уравнению, т.е. обращающую его в тождество по крайне мере в некотором промежутке изменения x :
(x) удовлетворяющую этому уравнению, т.е. обращающую его в тождество по крайне мере в некотором промежутке изменения x :
F(x, (x), (x)) 0.
5

Например, одним из решений уравнения |
y |
1 y 2 |
||||||||
является функция y sin x при x |
|
|
, |
|
. |
|
|
|||
2 |
2 |
|
|
|||||||
Если уравнение (1.5) можно разрешить относительно |
||||||||||
производной, то оно примет вид |
|
|
|
|
|
|
|
|||
|
y f (x, y). |
|
|
|
(1.6) |
|||||
Заменив производную отношением дифференциалов, |
||||||||||
уравнение (1.6) можно записать в форме |
|
|
|
|
||||||
|
dy |
f (x, y). |
|
|
|
(1.7) |
||||
|
|
|
|
|
|
|||||
|
dx |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Частным случаем уравнения (1.6) |
является простейшее |
|||||||||
дифференциальное уравнение y |
f (x). |
|
|
|
|
|||||
Общим решением уравнения (1.6) |
или (1.7) |
называется |
||||||||
дифференцируемая по x функция |
|
|
|
|
|
|
|
|||
|
y |
(x,C) , |
|
|
|
|
|
|
(1.8) |
|
зависящая от числового |
параметра |
|
C (“произвольной |
|||||||
постоянной”), если она является решением дифференциального уравнения при любых допустимых значениях этого параметра.
Решение, полученное из общего решения (1.8) при конкретном значении параметра C , называется частным
решением дифференциального уравнения. |
|
|
|
|
|||||
Соотношение вида |
|
|
|
|
|
|
|||
|
|
|
Ф(x, y,C) 0 , |
|
|
|
|
(1.9) |
|
определяющее общее решение как неявную функцию x |
и C , |
||||||||
называется общим интегралом уравнения (1.5) или (1.6). |
|
||||||||
Частным интегралом дифференциального уравнения (1.5) |
|||||||||
или (1.6) |
называется соотношение |
вида |
(1.8) |
при |
|||||
фиксированном значении параметра C . |
|
|
|
|
|||||
Если |
рассматривать |
x и |
y |
как |
прямоугольные |
||||
координаты точки на плоскости, то |
решению |
y |
(x,C) |
||||||
уравнения |
(1.7) |
или |
(1.5) |
при |
фиксированном |
значении |
|||
постоянной |
C |
будет |
соответствовать |
некоторая |
кривая на |
||||
плоскости |
XOY , которая |
называется |
интегральной |
кривой |
|||||
6

дифференциального уравнения (1.7) или (1.5). Придавая произвольной постоянной C разрешенные значения, получим семейство (бесконечное множество) интегральных кривых, каждой из которых соответствует определенное значение
постоянной C . |
|
|
Например, дифференциальное уравнение y x |
y 0, |
как |
легко проверить, имеет общее решение y Cx , |
C |
. |
Интегральными кривыми этого уравнения являются прямые, проходящие через начало координат. Точка (0,0) является особой точкой дифференциального уравнения. В этой точке уравнение не устанавливает никакого соотношения между x, y
и y . |
|
|
|
Дифференциальное уравнение |
dy |
f (x, y) устанавливает |
|
dx |
|||
|
|
||
зависимость между координатами |
|
точки, через которую |
проходит интегральная кривая, и угловым коэффициентом
касательной dy к графику этой кривой в той же точке. Зная x dx
и y можно вычислить f (x, y) . Следовательно, можно вычислить dydx . Сопоставляя каждой точке области, в которой
определено дифференциальное уравнение, вектор, направленный по касательной к графику решения, мы тем самым определяем поле направлений. Интегральные кривые – это линии, имеющие в каждой своей точке направление, определяемое дифференциальным уравнением (направление поля). Схематически поле направлений, задаваемое некоторым уравнением, показано на рис. 1. С этой точки зрения решение дифференциального уравнения состоит в нахождении кривой на заданному в каждой точке направлению. Как видим из формулы (1.8), таких кривых на плоскости – семейство, получаемое при изменении параметра C .
7
Чтобы выделить определенную кривую из этого семейства, необходимо потребовать, чтобы линия проходила через некоторую заданную точку (x0 , y0 ).
y
|
0 |
x |
|
|
|
|
|
Рис. 1. Поле направлений, |
|
|
|
|
|
задаваемое дифференциальным уравнением. |
|
|
|
|
||
Пример. |
Вернемся к |
уже рассмотренному выше |
||||
дифференциальному уравнению, |
записав его в виде |
dy |
|
y |
. |
|
|
|
|||||
|
|
|
dx |
|
x |
|
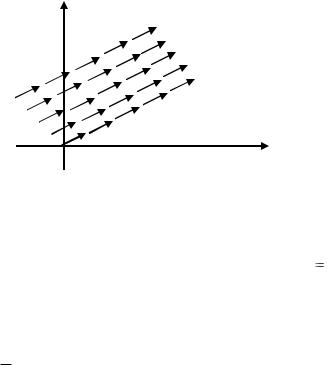
Построим поле направлений, определяемое этим уравнением. В каждой точке, отличной от точки (0,0) , угловой коэффициент касательной к некоторой интегральной кривой равен
отношению xy . То есть угловой коэффициент касательной
совпадает с угловым коэффициентом прямой, направленной из начала координат в ту же точку (x, y) . На рис. 2 показано поле направлений, задаваемое этим дифференциальным уравнением.
1.2. Задача Коши для дифференциального уравнения первого порядка. Теорема существования и единственности решения задачи Коши
1. Одной из важнейших задач в теории дифференциальных уравнений и в практических приложениях теории, является так называемая задача Коши. Для уравнения
(1.7)
8
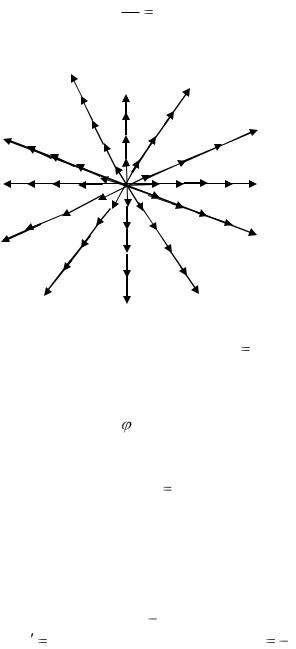
dy f (x, y) dx
задача Коши ставится следующим образом.
y 
x
Рис. 2. Поле направлений, определяемое уравнением y y
y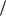 x .
x .
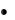 Задачей Коши (или начальной задачей) для дифференциального уравнения 1–го порядка называется задача нахождения решения y
Задачей Коши (или начальной задачей) для дифференциального уравнения 1–го порядка называется задача нахождения решения y 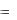 (x) этого уравнения, удовлетворяющего начальному условию
(x) этого уравнения, удовлетворяющего начальному условию
y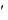
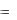 f (x, y) ,
f (x, y) ,
y(x0 ) y0 , |
(1.10) |
где x0 и y0 - заданные числа.
Геометрический смысл задачи Коши заключается в том, что ищется интегральная кривая дифференциального уравнения, проходящая через заданную точку плоскости
M 0 (x0 , y0 ) .
Например, функция y  2e x является частным решением
2e x является частным решением
уравнения y y при начальном условии y(0) |
2. |
9
