1270

ного моделирования для решения задачи численного расчета температуры резания и расчета тепловых полей в поверхностном слое обрабатываемой резанием детали в зависимости от изменения скорости резания и подачи.

Различают два основных метода численного решения математических уравнений: метод конечных элементов и метод конечных разностей, или сеточный метод.

Наиболее удобным для анализа процесса резания при протягивании оказался сеточный метод вычислений. Основная идея метода сеток заключается в том, что искомая непрерывная функция T = Т (x, y, τ) заменяется дискретными значениями Ti,kj в узлах ко-

ординатной сетки (i, j) в различных (k–х) временных слоях, а производные функции – соответствующими численными аналогами. В направлении оси Х нумерация узлов будет (j = 1, 2, ..., nx), а в направлении оси Y (i = 1, 2, ..., ny ). Здесь nx и ny – число узлов двумерной координатной сетки. Число k показывает, на сколько слоев (дискретных временных узлов) разбита непрерывная временная ко-

ордината τ (k = 1, 2, ..., nτ).

Такая дискретизация позволяет заменить исходные дифференциальные уравнения их численными аналогами и провести интегрирование этих уравнений численно. Численный расчет температуры резания при протягивании методом конечных разностей может производиться путем решения нестандартной задачи распределения температуры резания с использованием равномерной и неравномерной сетки.

Использование равномерной сетки существенно упрощает алгоритм вычислений, но имеет серьезные недостатки, самым главным из которых является достаточно жесткая зависимость размеров сетки и интервалов времени перемещения источника от величины температуропроводности и скорости передвижения теплового источника. Это снижает универсальность метода и может привести к погрешностям расчета, особенно нежелательным при расчете области под источником тепла.

91

Если же результаты решения температурной задачи используются в дальнейшем для расчета напряженно-деформированного состояния по той же сетке с равномерным разбиением, то решение такой комплексной задачи с применением ПЭВМ становится весьма проблематичным. В то же время для изучения процессов охлаждения в зоне за инструментом разбиение могло бы быть выполнено с большим шагом, чем под самым источником тепла.

Оптимальным выходом из этой ситуации служит сгущение сетки в тех областях, где искомая функция быстро возрастает / убывает, например, в зоне под источником тепла. Там, где функция стремится к асимптотическому решению (например, в достаточно отдаленной от источника энергии зоне), применяется разреженная сетка с относительно большим шагом по координате. Таким образом, неравномерная сетка позволяет точнее описать поведение функций в области высоких градиентов температур, а также существенно снизить затраты машинного времени ПЭВМ (рис. 29).

Применительно к рассматриваемой проблеме расчета температуры и теплового поля при скоростном протягивании деталей из жаропрочных сталей и сплавов протяжками из твердого сплава ВК8 задача формулируется следующим образом.

Принято, что увеличение скоростей протягивания и подач сопровождается значительным ростом тепловыделений в зоне резания и появлением высоких температур. Вследствие достаточно быстрого нагрева в локальной зоне вблизи источника тепла образуются высокие градиенты температурного поля в материале детали, что может существенно влиять на основные параметры качества поверхностного слоя и усталостную прочность.

Исследование температурных полей осложняется тем обстоятельством, что процесс протягивания необходимо рассматривать как нестационарный, описываемый математически с помощью дифференциальных уравнений параболического типа. Аналитический метод решения таких уравнений позволяет получить зависимость, с помощью которой можно определить максимальные значения температуры

92

по поверхности детали и ее распределение по глубине. В то же время решение таких уравнений обычными способами весьма затруднительно, так как для этого требуется знать двумерное распределение температуры. Поэтому решение подобной задачи возможно численным методом с использованием ПЭВМ.

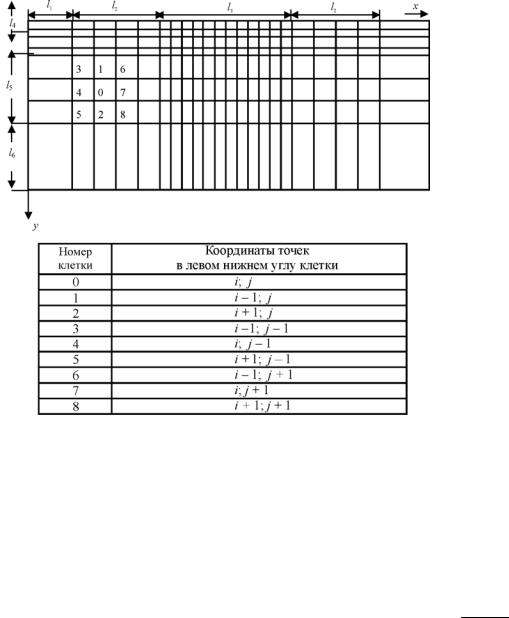
Рис. 29. Схема разбиения и кодирования координатной сетки при расчете температуры резания и тепловых полей численным методом

Общие закономерности расчета тепловых полей и распределения температуры резания, полученные для обычного токарного резца или для процесса шлифования, могут быть применены к расчету

93

температур и тепловых потоков при резании любым зубом такого многолезвийного инструмента, как протяжка. Однако процесс распространения теплоты в зоне резания многозубым инструментом имеет и свои особенности. Так как протяжка – многолезвийный инструмент, то можно предположить, что каждый последующий зуб протяжки будет работать при более высокой температуре резания изза подогрева поверхности впереди идущим зубом. В межзубовом пространстве происходит снижение температуры поверхности детали. Интенсивность этого снижения должна зависеть от скорости протягивания и величины шага между зубьями. Интересен также характер распространения и взаимовлияния температуры по глубине от каждого соседнего зуба. В связи с этим для расчета предложена двузубая схема протягивания (рис. 30).

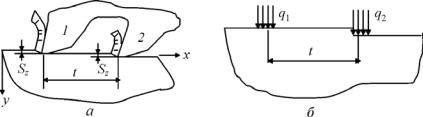
Рис. 30. Схемы расположения зубьев протяжки (а) и движения тепловых потоков от зубьев (б)

До сих пор были известны только работы А.Н. Резникова, который исследовал характер распространения температуры вдоль поверхности резания многолезвийным инструментом. Он установил, что подогрев последующих зубьев незначителен, и через один-два зуба температура резания стабилизируется на одном уровне, ненамного превышающем температуру резания первым зубом. Кроме того, при протягивании замков лопаток и пазов в дисках в контакте находится обычно не более двух зубьев.

94

На схеме (см. рис. 30, а) каждый зуб протяжки (№ 1 и 2) последовательно срезает металл толщиной Sz и находится друг от друга на расстоянии шага t. Последующий третий зуб протяжки имеет начальную температуру Тн. Система координат выбирается жестко связанной с протяжкой, а движение источника тепла моделируется как тепломассоперенос с заданным полем скоростей

где Vx, Vy – скорости перемещения источников тепла в направлении координатных осей; V – скорость перемещения протяжки.

В качестве начального условия принимается однородное распределение температуры по всей исследуемой области:

Расчет температур производится на основе известного уравнения теплопроводности, которое для рассматриваемой задачи записывается в следующем виде:

где C – постоянная теплопроводности; τ – время, с; λ – теплопроводность детали.

Для решения поставленной задачи уравнение (4) необходимо дополнить граничными условиями. На границе, по которой взаимодействуют оба зуба протяжки с обрабатываемой деталью, заданы тепловые потоки (граничное условие второго рода) (см. рис. 30, б):

Тепловые потоки q1 и q2, направленные в деталь, образуются на поверхности сдвига и на площадке контакта задней поверхности инструмента с деталью. Нужно учесть, что величина подачи Sz достаточно мала относительно шага t, что позволяет пренебречь различением между температурами вершины зуба и точки на конце плоскости сдвига.

95

На остальной части границы выполняются граничные условия теплообмена третьего рода (закон Ньютона):

где α – коэффициент теплоотдатчи поверхности детали; Tc – температура окружающей среды.

Краевые и граничные условия (5), (6) вместе с уравнением (4) образуют так называемую задачу Коши. Численное решение задачи теплопроводности строится на неравномерной, сгущенной в области приложения двумя зубьями температурных нагрузок разностной сетке (см. рис. 29). Уравнение теплопроводности интегрировалось при этом по явной разностной схеме:

2

где Tij – температура в узле (ij); yij – координата узла (ij) по оси y. Для внутренних узлов сетки (см. рис. 29) численные аналоги

производных д2T/дx2 и д2T/дy2 по пространственным координатам имеют следующий вид (разностная схема второго порядка):

где xij – координата узла (ij) по оси x.

Производная по временной координате имеет следующий вид:

где знак «+» означает следующий шаг по времени, «–» – предыдущий; Δτ – шаг интегрирования по временной координате.

96

Тогда уравнение теплопроводности преобразуется в численном виде, и из него можно определить значение температуры в любом узле расчетной области следующим образом:

Повторяя процедуру решения уравнения (10) необходимое количество раз, можно рассчитать температуру в любой точке в любой момент времени. На первом шаге в качестве Tij− используются на-

чальные условия, т.е. Tij− = T0. Для решения этой задачи разработана

программа расчета, алгоритм которой представлен в виде блоксхемы на рис. 31. В разработанную программу расчета на ПЭВМ вводятся данные о теплофизических свойствах обрабатываемого материала, о времени и скорости обработки, о начальной температуре детали.

Входная информация включает порядок разбиения исследуемой области по осям х и y с конкретными координатами граничных узлов внутри интервалов и указанием числа разбиения отдельных участков расчетной сетки и шага по временной координате.

В результате расчета тепловых полей при протягивании различных жаропрочных сталей и сплавов получены следующие новые весьма интересные результаты. Установлено, что поверхностный слой металла при протягивании прогревается на очень незначительную величину: 0,1…0,2 мм, причем максимальная температура на этой глубине обычно не более 100…150 °С. После прохождения зуба протяжки температура на всей глубине поверхностного слоя снижается до начальной Тн.

97

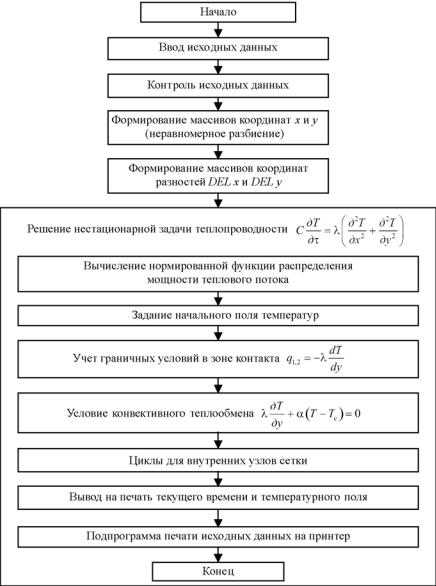
Рис. 31. Блок-схема алгоритма расчета температуры резания и тепловых полей при протягивании двузубой протяжкой

98

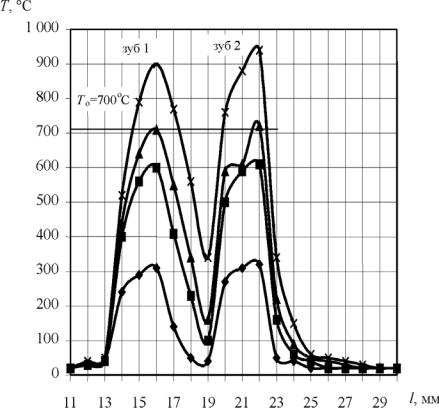
Результаты расчета распределения температуры при протягивании по глубине поверхностного слоя, типичное изображение которого представлено на рис. 32, показывают, что температура второго зуба всегда выше первого на 1…3 %, причем чем выше скорость протягивания, тем больше разность температуры. Максимальное

Рис. 32. Результаты расчета контактной температуры резания Т по длине l образца при протягивании двузубой протяжкой на различных скоростях резания

ЭИ787-ВД при Sz = 0,06 мм/зуб и ВК8

10 м/мин, 18 м/мин, 24 м/мин, 30 м/мин

99

значение температуры на поверхности детали 1 130 °С получено при скорости резания 30 м/мин и подаче 0,1 мм/зуб. С увеличением скорости протягивания с 10 до 30 м/мин при одной и той же подаче Sz градиент падения температуры Т по глубине поверхности увеличивается в 2–3 раза.

Сравнивая результаты предыдущих расчетов оптимальных скоростей и расчета температуры резания, можно наглядно видеть подтверждение того, что протягивание на оптимальных скоростях резания происходит при одной и той же оптимальной для данного обрабатываемого материала температуре резания. Так, при анализе полученных термограмм установлено, что протягивание сплава ЭИ787-ВД с подачей 0,02 мм/зуб на оптимальной скорости резания 30 м/с, с подачей 0,06 мм/зуб на оптимальной скорости резания 24 м/мин (см. рис. 32) и с подачей 0,1 мм/зуб на оптимальной скорости 14 м/мин происходит при одной и той же температуре резания: в среднем То = 700 °С, которая и принята за оптимальную. При этом разброс значений оптимальной температуры резания То не более 1…2 %. Это свидетельствует о достаточно высокой точности расчетно-аналитического метода. После прохода первого зуба протяжки поверхностная температура начинает резко уменьшаться, но не достигает начального значения температуры Тн, т.к. приходит новый приток тепла из зоны резания вторым зубом. При уменьшении скорости резания до 10 м/мин и подаче 0,06 мм/зуб поверхностная температура снижается между двумя зубьями с 310 до 50 °С (см. рис. 32). При более высокой скорости резания (30 м/мин) и той же подаче температура резания на поверхности снижается между двумя зубьями с 906 до 336 °С, т.е. почти в два раза.

Аналогичные результаты были получены при математическом расчете температуры резания и тепловых полей и для протягивания жаропрочных сталей и титановых сплавов. При этом получены расчетные значения оптимальных температур резания, соответствующие оптимальным скоростям резания.

100