
Статистические исследования контроля качества в автоматизированных
..pdf
4.5.ОПРЕДЕЛЕНИЕ ОШИБКИ ВЫБОРКИ
Врезультате статистической обработки данных могут возникнуть ошибки наблюдения, получаемые вследствие расхождения между величиной какого-либо показателя, найденного при статистическом наблюдении данных, и действительными его размерами. Кроме того, возникают ошибки регистрации и ошибки репрезентативности, зависящие от причин их возникновения.
Ошибки регистрации – результат ошибочной записи и неправильного установления фактов в процессе наблюдения и связаны со случайными и систематическими ошибками.
Случайные ошибки – результат регистрации в процессе контроля или опроса средств измерений при автоматическом контроле.
Систематические ошибки могут быть преднамеренными и непреднамеренными. Преднамеренные ошибки связаны с сознательным искажением результатов контроля. Непреднамеренные ошибки связаны с небрежностью, невнимательностью при ручном и автоматизированном контроле.
Ошибки репрезентативности (представительности) – резуль-
тат обследования, при котором объем выборки недостаточен для полного воспроизводства генеральной совокупности и, как следствие, неполного обследования контролируемого параметра. Они могут быть случайными и систематическими.
Разность между характеристиками выборочной и генеральной совокупности определяют ошибки выборки. Для среднего значения
предельная ошибка выборки вычисляется по формуле
x = x − x ,
где x= xi / N х, Nx – генеральная совокупность.
Грубые ошибки и промахи обнаруживают и исключают из расчётов следующим образом:
♦ находят среднее арифметическое x результата n-кратного измерения величины хi;
71

♦определяют среднее квадратическое отклонение S;
♦вычисляют вспомогательную величину t(S) (табл. 4.3).
Таблица 4 . 3
Значения вспомогательной величины t(S)
Параметр |
|
|
|
Число измерений, n |
|
|
|
|||
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
t(S) |
15,56 |
4,97 |
3,56 |
|
3,04 |
2,78 |
2,62 |
2,51 |
2,43 |
2,37 |
|
|
|
|
|
|
|
|
|
|
|
При |хi – x | > t(S) результат измерения хi является грубой ошибкой, поэтому его исключают из расчётов и среднее значение x вычисляютзановодля оставшихсядостоверныхрезультатов измерения.
Ошибки (промахи) могут быть исключены из генеральной совокупности с помощью следующего правила:
♦если некоторое измерение xi внушает сомнение в его принадлежности к генеральной совокупности, в этом случае определяются значения x и S генеральной совокупности без сомнительных измерений;
♦вычисляется коэффициент k = (xi – x )/S.
Если k больше допустимого значения, то делается вывод о том, что xi не принадлежит к генеральной совокупности.
Часть значений допустимых k можно найти по числу измере-
ний n по табл. 4.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица |
4 . 4 |
||
Значения допустимых k в зависимости от числа измерений |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Параметр |
|
|
|
Число измерений, n |
|
|
|
|
|||
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
25 |
|
|
|
||||||||||
Значение k |
1,49 |
1,94 |
2,22 |
2,41 |
2,55 |
2,66 |
2,75 |
2,82 |
2,88 |
|
3,01 |
В литературе известны также критерии 3s, Граббса (Смирнова), Шарлье, Шовенэ, Диксона и др., которые позволяют исключить грубые промахи.
72
Пример 4.2. Определить ошибку выборки для параметра размера детали, численные значения которого представлены ниже.
Выборка значений параметра размера детали
Значение параметра |
Число измерений, n |
23,25 |
1 |
|
|
23,85 |
2 |
|
|
23,86 |
5 |
|
|
23,88 |
9 |
|
|
23,89 |
10 |
|
|
23,9 |
11 |
|
|
23,91 |
13 |
|
|
23,92 |
11 |
|
|
23,93 |
12 |
|
|
23,94 |
8 |
|
|
23,95 |
8 |
|
|
23,96 |
6 |
|
|
23,97 |
2 |
|
|
23,98 |
2 |
|
|
23,99 |
1 |
|
|
Решение. Определим ошибку рассматриваемой выборки через вспомогательную величину t(S), для чего рассчитаем среднее арифметическое значение n-кратного измерения размера детали: x = 23,90941.
Среднее квадратическое отклонение: S = 0,07299. Вспомогательную величину t(S) получим экстраполяцией
существующей зависимости (табл. 4.3), которая будет представлена ниже (в рамках программного расчёта, подразд. 4.6): для n = 101t(S) = 0,28995.
Таким образом, результат измерения х1 является грубой ошибкой:
|х1 – x | > 0,28995,| – 0,65941| > 0,28995.
73

По этой причине его необходимо исключить из расчётов и заново определить значение x для оставшихся достоверных результатов измерения.
Далее произведём расчёт ошибки выборки с использованием коэффициента k.
Согласно второму способу получаем, что для x1 = 23,25 величина k > kдоп (табл. 4.4), поскольку
k = (x1 – x )/S = (23,25 – 23,90941)/0,07299 = –9,03423; | –9,03423| > 6,02.
При этом допустимая величина k = 6,02 (определена методом экстраполяции существующей зависимости, по аналогии с подразд. 4.6), поэтому x1 представляет собой также грубую ошибку выборки, что идентично полученному выше результату.
4.6.ОПРЕДЕЛЕНИЕ ОШИБКИ ВЫБОРКИ
ВПРОГРАММЕ «STATISTICA 8»
Определим ошибки выборки случайной величины в программном продукте «STATISTICA 8», используя в качестве изучаемого признака (xi) размер детали (приложение 1 «Исходные данные»). При этом формирование (загрузка) исходных данных (101 значение согласно варианту) осуществляется аналогичным способом, описанным выше (см. рис. 3.8).
Поскольку в программе отсутствует полноценный модуль определения ошибок выборки, напишем макрос (программный код)
в среде «STATISTICA VISUAL BASIC» (приложение 5), позво-
ляющий это осуществить с учётом имеющегося в распоряжении исследователя функционала.
На рис. 4.8 представлены исходные данные и результаты определения объёма и ошибки выборки, полученные на основе программного кода (тёмным цветом выделены параметры, вводимые исследователем вручную).
74
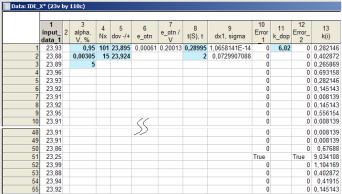
Рис. 4.8. Исходные данные и результаты определения объёма и ошибки выборки
Приведем краткое описание основных переменных для данной таблицы:
♦«input_data_1» – исходные данные (101 значение);
♦«alpha», «V» и «%» – доверительная вероятность, коэффи-
циент вариации, процент бесповторного отбора (серийная выборка) соответственно;
♦«Nx» – объём выборки (101 значение) и общее число се-
рий (15);
♦«dov – /+» – нижняя и верхняя доверительные границы;
♦«e_otn» – относительная ошибка;
♦«e_otn/V» – соотношение относительной ошибки и коэффициента вариации;
♦«t(S)» – вспомогательная величина для определения ошибки выборки;
♦ «t» – параметр, определяемый уровнем вероятности (для
P = 0,954 параметр t = 2);
♦«dx1», «sigma» – предельная ошибка выборки и среднее квадратическое отклонение («0» – ошибка не найдена, «True» – ошибка обнаружена);
♦«Error_1» – ошибка выборки, определенная способом № 1;
75

♦«k_dop» – допустимое число, зависящее от числа измерений;
♦«Error_2» – ошибка выборки, определенная способом № 2 («0» – ошибка не найдена, «True» – ошибка обнаружена);
♦«k(i)» – расчётное значение числа k.
При этом, поскольку для используемых в расчётах значений выборки вспомогательная величина t(S) и допустимое число k выходят за область известных данных (табл. 4.3 и 4.4), осуществлялась экстраполяция на основе следующих зависимостей:
y1 |
= 10,807x1–0,784 |
R² = 0,8768; |
y2 |
= 1,5586x20,2928 |
R² = 0,9855, |
где y1 и y2 – величины t(S) и k соответственно; x1 и x2 – количество измерений (n) для первого и второго способов расчёта ошибки выборки; R – коэффициент детерминации, описывающий степень зависимости рассматриваемых величин.
В результате определена ошибка выборки (см. рис. 4.8), которая соответствует51-й строке столбца «input_data_2» илизначению23,25.
4.7. СОБСТВЕННО СЛУЧАЙНАЯ ВЫБОРКА
Выборочное наблюдение относится к разновидности несплошного наблюдения, цель которого – по отобранной части единиц дать характеристику всей совокупности единиц. Необходимо, чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц).
Используя теорему П.Л. Чебышева можно вычислить величину μx , выражающую среднее квадратическое отклонение выборочной средней от математического ожидания:
μ |
|
= |
S |
, |
(4.1) |
|
|
||||
x |
|||||
|
|
|
N |
|
|
которую называют средней ошибкой выборки.
76

С учетом выбранного уровня вероятности и соответствующего ему значения t (выбирается по табл. П8) предельная ошибка выборки составит:
|
|
|
|
|
|
= t μ |
|
|
. |
|
|
(4.2) |
||
|
|
|
|
|
x |
x |
||||||||
Генеральная средняя при заданной вероятности с учетом (4.1) |
||||||||||||||
и (4.2) будет находиться в следующих границах: |
|
|||||||||||||
|
|
− |
|
≤ x ≤ |
|
+ |
|
. |
(4.3) |
|||||
x |
x |
|||||||||||||
|
x |
x |
||||||||||||
Пример 4.3. При выборочном обследования жилищных условий жителей города на основе собственно-случайной повторной выборки, получены следующие данные:
Данные выборочного обследования жилищных условий жителей города
Общаяплощадь |
|
|
|
|
|
|
|
жилищ, |
До5,0 |
5,0…10,0 |
10,0…15,0 |
15,0…20,0 |
20,0…25,0 |
25,0…30,0 |
30,0 |
приходящаяся |
иболее |
||||||
на1 чел., кв. м. |
|
|
|
|
|
|
|
Числожителей |
8 |
95 |
204 |
207 |
210 |
130 |
83 |
Решение. Рассмотрим определение границ генеральной средней, в данном случае – средней площади жилищ в расчёте на 1 чел. в целом по городу, исходя из данных выборочного обследования. Вначале необходимо рассчитать выборочную среднюю величину и дисперсию изучаемого признака для определения средней ошибки выборки (табл. 4.5).
В случае, когда данные сгруппированы по интервалам, т.е. представлены в виде интервальных рядов распределения, при расчёте средней арифметической в качестве значения признака принимают середину интервала, исходя из предположения о равномерном распределении единиц совокупности на данном интервале. Расчёт ведется по формуле
77
|
n |
|
|
х= |
xi |
mi |
|
i=1 |
|
, |
|
n |
|
||
mi
i=1
где xi – середина интервала.
Таблица 4 . 5
Расчёт средней (полезной) площади жилищ, приходящейся на 1 чел., и дисперсии
Общая(полезная) |
Число |
Середина |
|
xi2 mi |
площадьжилищ, |
xi · mi |
|||
приходящаясяна1 чел., м2 |
жителейmi |
интервалаxi |
|
|
До5,0 |
8 |
2,5 |
20,0 |
50,0 |
5,0…10,0 |
95 |
7,5 |
712,5 |
5343,75 |
10,0…15,0 |
204 |
12,5 |
2550,0 |
31875,0 |
15,0…20,0 |
270 |
17,5 |
4725,0 |
82687,5 |
20,0…25,0 |
210 |
22,5 |
4725,0 |
106312,5 |
25,0…30,0 |
130 |
27,5 |
3575,0 |
98312,5 |
30,0 иболее |
83 |
32,5 |
2697,5 |
87668,75 |
Итого: |
1000 |
– |
19005,0 |
412250,0 |
Внашем примере
х= 19 005,0 = 19,0 м2 . 1000
Дисперсию определим по формуле
|
|
n |
|
|
|
|
|
|
xi |
2 mi |
|||
|
S 2 = |
i=1 |
|
|
− х2 . |
|
|
|
|
|
|||
|
|
|
N |
|||
Тогда получаем |
|
|
|
|
|
|
S 2 = |
412 250 |
− 19,02 = 51,25. |
||||
1000 |
||||||
|
|
|
|
|||
78

Откуда получаем значение выборочного среднего квадратичного отклонения
S = 7,16 м2.
Используяформулу (4.1), определим среднююошибку выборки:
μ |
|
= |
7,16 |
= 0,23 м2 . |
|
|
|||
x |
1000 |
|||
|
|
|
|
Тогда предельная ошибка выборки согласно (4.2) с вероятностью 0,954 (t = 2) составит:
x = 2 0,23 = 0,46 м2 .
По формуле (4.3) определяем границы генеральной средней:
19,0 − 0,46 ≤ x ≤ 19,0 + 0,46 или 18,54 ≤ x ≤ 19,46 .
По результатам исследования с вероятностью 0,954 можно сделать вывод, что средний размер общей площади, приходящейся на 1 человека, в целом по городу лежит в пределах от 18,5 до 19,5 м2.
Для учета бесповторности отбора при расчёте средней ошибки необходимо ввести поправку:
μ |
|
= |
S2 |
|
− |
N |
|
(4.4) |
|
|
1 |
|
. |
||||
|
|
|
||||||
x |
N |
|
||||||
|
|
|
|
|
Nx |
|
||
На основании представленных в табл. 4.5 данных 5%-ного бесповторного отбора (следовательно, генеральная совокупность включает 20 000 ед.) средняя ошибка выборки согласно (4.4) будет несколько меньше:
μ |
|
= |
51,25 |
|
− |
1000 |
= 0,22 м |
2 |
|
|
|
|
1 |
|
|
|
. |
||||
x |
1000 |
20000 |
|
|||||||
|
|
|
|
|
|
|
|
|
||
Как результат уменьшится и предельная ошибка выборки, а это согласно формуле (4.3) приведет к уменьшению границ гене-
79
ральной средней совокупности. При относительно большом проценте выборки получим более значительное влияние поправки на бесповторность отбора.
4.8. СЕРИЙНАЯ ВЫБОРКА
При сплошном обследовании продуктов серийная выборка группединиц(серий) формируетсялибо случайно, либомеханически.
За единицу отбора принимается группа или серия в отличие от отдельной единицы генеральной совокупности, рассмотренной ранее.
Серийную выборку удобнее применять в том случае, когда единицы генеральной совокупности образованы объединением продуктов в небольшие более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки в соответствии со способом «в упаковке» с определенным количеством готовой продукции, партии отпускаемой продукции и т.д.
Например, в Великобритании серийный отбор используется при обследовании населения, когда серией являются домохозяйства, объединенные общим почтовым индексом. Выборка индексов производится в случайном порядке, а исследование проводят с данными тех домохозяйств, которые имеют индекс, попавших в выборочную совокупность почтовых отделений.
Серийная выборка по сравнению с другими способами формирования выборочной совокупности в некоторых случаях имеет не столько методологические, сколько организационные преимущества. Например, при обследовании школьников. С организационной точки зрения достаточно сложно опрашивать отдельных учеников из разных классов. Значительно проще из общего списка всех классов всех школ округа сформировать выборку классов, а внутри отобранных классов провести 100%-ное обследование учащихся.
Следует учитывать особенность серийного отбора, при котором внутри отобранных групп исследуемого признака анализируются все полученные данные, поэтому ошибки выборочного наблюдения практически не зависят от внутригрупповой вариации
80
