
Статистические исследования контроля качества в автоматизированных
..pdf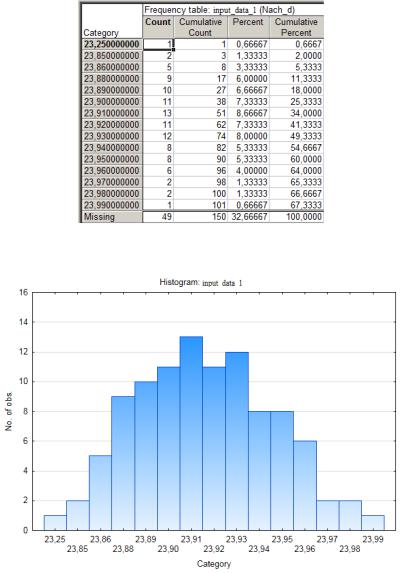
Рис. 3.12. Таблица частот
Рис. 3.13. Гистограмма распределения случайной величины
41
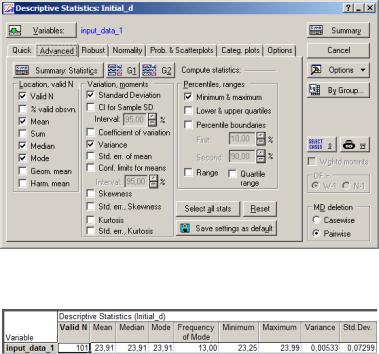
Рис. 3.14. Окно выбора параметров для расчёта мер положения и рассеяния кривой распределения
Рис. 3.15. Результат расчёта данных
стандартное отклонение, «Variance» – дисперсия, «Minimum&maximum» – минимальное и максимальное значения (для определения размаха выборки).
После нажатия на кнопку «Summary: statistics» получим следующий результат (рис. 3.15).
3.6. КАТЕГОРИИ СРЕДНИХ ВЕЛИЧИН
Средние величины делятся на две основные категории:
♦ степенные средние; к ним относятся известные и часто применяемые: средняя арифметическая величина, средняя квадратическая и средняя геометрическая;
42

♦структурные средние, в качестве которых выступают мода
имедиана (подразд. 3.4).
Степенными средними являются средние величины, вычисляемые по формуле
|
|
n |
||
|
= k |
xik |
||
|
i=1 |
, |
||
x |
||||
|
||||
N
где xi – индивидуальное значение исследуемого параметра; n – число единиц совокупности; k – показатель степени средней величины.
Взвешенная средняя величина считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:
|
|
n |
|
|
|
= k |
xik mi |
|
|
|
i=1 |
, |
||
x |
||||
n |
||||
взв |
|
|||
|
|
mi |
|
|
|
|
i=1 |
|
|
где xi – значение (варианта) осредняемого признака или срединное значение интервала, в котором измеряется варианта; mi – частота повторения индивидуальных значений признака (вес), показывающая, сколько раз встречается i-е значение осредняемого признака.
Формула средней величины определяется значением степени применяемой средней. Формулы расчёта степенных средних включают показатель степени k. В зависимости от его значения различают следующие виды степенных средних:
♦средняя гармоническая, если k = –1;
♦средняя геометрическая, если k →0;
♦средняя арифметическая, если k = 1;
♦средняя квадратическая, если k = 2;
♦средняя кубическая, если k = 3 и т.д.
43

Если рассчитать все виды средних величин для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности: с увеличением показателя степени k увеличивается и соответствующая средняя величина:
x гарм < x геом < x ариф < x кв < x куб.
Формулы расчёта простой и взвешенной средних величин примут вид:
1. Средняя гармоническая (Harmonisches Mittel, Harmonic mean) (k = –1):
простая: |
|
= |
N |
; |
x |
|
|||
1 / xi |
|
|
|
mi |
|
|
|
взвешенная: |
x = |
|
, |
|||
mi |
/ |
|
||||
|
|
|
xi |
|||
где mi – вес средней гармонической величины, равный произведению индивидуального значения параметра на его частоту (обычную).
Пример 3.3. Согласно приведённым выше формулам осуществим расчёт средней гармонической величины заработной платы сотрудников по отделам, используя данные табл. 3.3 и 3.4.
|
|
|
Таблица 3 . 3 |
|
|
Данные о заработной плате по отделам организации N |
|||
|
|
|
|
|
Отдел |
Заработная плата |
Численность, чел. |
|
|
по отделу, у.е. |
|
|||
|
|
|
|
|
1 |
|
1500 |
40 |
|
2 |
|
1600 |
80 |
|
3 |
|
1700 |
130 |
|
В этом случае среднюю зарплату по организации определяем, используя среднюю гармоническую простую:
|
= |
|
|
3 |
|
|
|
= 1596 у.е. |
||
x |
|
|
|
|
|
|
|
|||
1 |
+ |
|
1 |
+ |
|
1 |
||||
|
|
|
||||||||
|
|
1500 |
1600 |
1700 |
|
|||||
|
|
|
|
|
||||||
44
|
|
|
Таблица 3 . 4 |
|
|
Данные о заплате по отделам организации N |
|||
|
|
|
|
|
Отдел |
|
Заработная плата по отделу, |
Фонд заработной платы, |
|
|
у.е. |
у.е. |
|
|
|
|
|
||
1 |
|
1500 |
60 000 |
|
2 |
|
1600 |
128 000 |
|
3 |
|
1700 |
221 000 |
|
Однако часто данные имеются в другом виде (см. табл. 3.4). Тогда для расчёта средней зарплаты по организации применяется средняя гармоническая взвешенная:
|
|
= |
60 000 +128 000 + 221000 |
=1636 у.е. |
|||||
x |
|||||||||
|
60000 |
|
128 000 |
|
221000 |
||||
гарм.взв |
|
+ |
+ |
|
|||||
|
|
|
1500 |
1600 |
1700 |
|
|||
|
|
|
|
|
|
||||
Среднюю гармоническую часто рассматривают как величину, обратную средней арифметической.
2. Средняя геометрическая (Geometrisches Mittel, Geometric mean) (k = 0):
простая: |
|
= n x1 x2...xn |
=m−1 |
yn |
; |
|||
x |
||||||||
|
||||||||
|
|
|
|
|
|
y0 |
||
взвешенная: |
|
= m x1m1 |
x2m2 ... xnmn , |
|||||
x |
||||||||
где x1, xn – цепные коэффициенты роста, x1 = y1/y0, x2 = y2/y1, …, xn = yn/yn–1; n – число этих коэффициентов роста; m – количество уровней ряда; y0 – значение начального уровня ряда; yn – значение конечного уровня ряда.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчёте средней геометрической индивидуальные значения признака представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня к предыдущему.
45

Средняя геометрическая применяется тогда, когда используются операции, связанные умножением/ делением, а не сложением/ вычитанием.
Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.
Пример 3.4. Найти среднегодовой темп роста и прироста по данным, представленным ниже.
|
Темпы роста объёма сбыта по фирме N |
|
|
Годы |
Произведено услуг, тыс. у.е. (темпы роста, %) |
2008 |
1900 |
2009 |
1938 (1938/1900 = 1,02) |
2010 |
1976 (1,02) |
2011 |
1957 (0,99) |
2012 |
1995 (1,02) |
Тогда среднегодовой темп роста (Wachstumstempo, Rate of Growth) определится как
W = 4 1,02 1,02 0,99 1,02 = 1,0123 = 101,23 %.
Среднегодовой темп прироста (Zuwachsrate, Rate of increment)
определяется по формуле
R = Среднегодовой темп роста – 1.
В нашем примере R = 1,0123 – 1 = 0,0123 или 1,23 %.
Среднегодовой темп роста и среднегодовой темп прироста можно получить, исходя и из абсолютных значений:
W =m−1 yn = 4 1995 =1,0123. y0 1900
46

Тогда получим:
R = 1,0123 – 1 = 0,0123 или 1,23 %.
Форма средней геометрической взвешенной в практических расчётах применяется крайне редко.
3. Средняя арифметическая (Arithmetisches Mittel, Arithmetic mean) (k = +1):
|
|
|
|
n |
|
|
|
||
|
|
|
xi |
|
|||||
простая: |
|
= |
|
i =1 |
|
; |
|
||
x |
|
||||||||
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
взвешенная: |
|
xi mi |
|
||||||
|
= |
i =1 |
. |
||||||
x |
|||||||||
|
mi |
||||||||
|
|
|
|
|
|
|
|
||
Средняя арифметическая простая используется тогда, когда значение признака относится к отдельным единицам наблюдения или к равновеликим группам единиц.
Пример 3.5. Произвести расчёт средней арифметической величины заработной платы работников бригады, используя представленные ниже данные.
Заработная плата работников бригады
Работник |
|
|
Заработная плата, у.е. |
||
№ 1 |
|
|
1500 |
||
№ 2 |
|
|
1600 |
||
№ 3 |
|
|
1700 |
||
|
|
= |
1500+1600 +1700 |
=1600 у.е. |
|
x |
|||||
|
|
|
3 |
|
|
Средняя арифметическая взвешенная применяется тогда, когда отдельные значения признака встречаются с разной частотой или когда группы не являются равновеликими.
47
Далее рассчитаем среднюю арифметическую величину заработной платы работников по цехам предприятия (табл. 3.5).
|
|
|
|
|
|
Таблица 3 . 5 |
|
|
|
Заработная плата по цехам предприятия |
|||
|
|
|
|
|
|
|
Цех |
|
|
|
Заработная плата |
|
Количество работающих |
|
|
|
по цеху, у.е. |
|
в цехе, чел. |
|
|
|
|
|
|
||
1 |
|
|
|
1500 |
|
40 |
2 |
|
|
|
1600 |
|
80 |
3 |
|
|
|
1700 |
|
130 |
|
|
|
|
=1500 40+1600 80 +1700 130 =1636 у.е. |
||
|
|
x |
|
|||
|
|
взв |
40+80 |
+130 |
||
|
|
|
|
|||
4. Средняя квадратическая (Quadratisches Mittel, Quadratic mean) (k = 2):
|
|
|
|
|
n |
|
|
|
|
простая: |
|
= |
|
|
xi2 |
||||
|
|
|
i=1 |
|
; |
|
|||
x |
|||||||||
|
|
n |
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n |
|||
|
|
|
|
|
|
xi2mi |
|||
|
|
|
|
|
|
i=1 |
|||
взвешенная: |
x = |
||||||||
|
|
. |
|||||||
|
n |
||||||||
|
|
|
|
|
|
mi |
|||
i=1
Пример 3.6. Используя данные о заработной плате работников бригады в примере 3.5 и табл. 3.5, произвести расчёт средней квадратической величины заработной платы:
|
|
|
|
= |
15002 +16002 +17002 |
=1602 у.е., |
|
|
|
|
x |
3 |
|||
|
|
|
|
|
|
|
|
|
= |
15002 |
40 +16002 80 +17002 130 |
= 1638 у.е. |
|||
x |
|
|
|
250 |
|
||
|
|
|
|
|
|
|
|
48
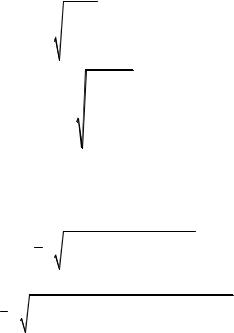
Средняя квадратическая применяется в тех случаях, когда исходные значения x могут быть как положительными, так и отрицательными, например, при расчёте средних отклонений, а также при расчёте показателей вариации значений х и если нужно сохранить неизменной сумму квадратов исходных величин.
5. Средняя кубическая (Kubisches Mittel, Cubic mean) (k = 3):
|
|
|
|
|
n |
|
|
|
|
|
|
= 3 |
|
xi3 |
|||||
простая: |
|
|
i=1 |
|
; |
|
|||
x |
|||||||||
|
n |
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n |
|||
|
|
|
|
|
|
xi3mi |
|||
|
|
|
|
|
|
i=1 |
|||
взвешенная: x = 3 |
|||||||||
|
|
. |
|||||||
|
n |
||||||||
|
|
|
|
|
|
mi |
|||
i=1
Пример 3.7. Используя данные о заработной плате работников бригады в примере 3.5 и табл. 3.5, произвести расчёт средней кубической величины заработной платы:
x = 3 15003 +16003 +17003 = 1604 у.е.; 3
x = 3 15003 40 +16003 80 +17003 130 = 1639 у.е. 250
Средняя кубическая применяется крайне редко, например, при расчёте индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН, а также если нужно сохранить неизменной сумму кубов исходных величин.
Также используется система индексов Фостера – Грира – Торнбека (Foster – Greer – Thornback, FGT), разработанная в 1984 г.
для оценки распространенности и глубины бедности.
49
Наиболее известный и распространенный вид средней – средняя арифметическая величина. Среднюю гармоническую часто рассматривают как величину, обратную средней арифметической.
Условия применения средних величин в анализе:
♦однородность статистической совокупности. Если при воздействии некоторых случайных факторов исследуемая величина имеет большой разброс данных (слишком большие и слишком маленькие) относительно большинства параметров, тогда слишком большие будут влиять на среднюю величину, а слишком маленькие – увеличивать объем вычислений, практически не влияя на значение средней. В этом случае средняя величина не будет отражать характерную для данной совокупности параметров величину признака.
В наличии неоднородного исследуемого явления данные разбивают на группы с однородными элементами. В таких группах рассчитывают сначала средние, которые называются групповые средние, и они будут выражать наиболее типичную величину явления в каждой группе. После этого по групповым средним рассчитывается общая средняя величина, которая и будет характеризовать явление в целом.
На практике, однако, выполнение данного условия не является корректным. Например, расчёт величины среднего потребления электроэнергии, включая высокоэнергетические отрасли (металлургия, алюминиевое производство) и низкоэнергетические (жилой сектор, медицинские учреждения, административные здания);
♦достаточное количество единиц в выборке. Достаточность является решающим условием при выборе выборочного наблюдения для обеспечения репрезентативности выборки;
♦исключение большого расхождения между максимальным
иминимальным значениями исследуемого параметра. При больших расхождениях между крайними значениями и средней величиной необходимо проверить на соответствие максимальных значений данной выборки, а также проверить их на предмет ошибки или про-
50
