
Статистические исследования контроля качества в автоматизированных
..pdfВыполнение этого требования необходимо для того, чтобы уменьшить влияние погрешностей измерений. Например, для k = 7 расчётная цена разряда при R = 0,13 мм, h = 0,13/7 = 0,0185 мм, принимаем h = 0,02 мм. Заметим, что округление цены разряда должно быть минимальным и допустимо в большую сторону.
Для удобства построения кривой результаты разбиений на интервалы и частоты, соответствующие этим интервалам, сводятся в табл. 5.2. Частоты, соответствующие границам интервалов, распределяют между ними: соответствующие нижней границе относят к предшествующему интервалу; соответствующие верхней границе – к последующему интервалу. Масштаб графиков – по оси абсцисс произвольный, а по оси ординат – отношение максимальной высоты к ширине основания как 5:8.
|
|
|
|
|
Таблица 5 . 2 |
|
|
Определение частот и частостей |
|
|
|||
|
|
|
|
|
|
|
Номер |
Интервалы, мм |
Частота, |
mi |
|
Частость, |
|
интервала |
от |
до |
|
mi / N |
||
|
|
|
||||
1 |
19,85 |
19,87 |
3 |
|
|
0,03 |
2 |
19,87 |
19,89 |
16 |
|
|
0,16 |
3 |
19,89 |
19,91 |
22 |
|
|
0,22 |
. |
. |
. |
. |
|
|
. |
. |
. |
. |
. |
|
|
. |
. |
. |
. |
. |
|
|
. |
7 |
19,97 |
19,99 |
2 |
|
|
0,02 |
|
|
|
∑100 |
|
|
|
Следующим этапом является построение кривой распределения. Она строится в координатах «mi» – «R». Масштабы по осям выбираются произвольные, удобные для построения. По оси абсцисс откладывается размах R (интервалы k), из середины интервала по вертикали откладываются соответствующие им значения чисел деталей, имеющих погрешности в пределах интервала. Полученные точки соединяются отрезками прямой (рис. 5.3).
91
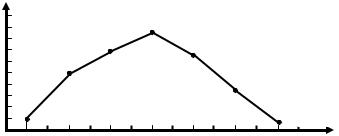
Практическая кривая (полигон) служит для первой приближенной оценки точности процесса и решения вопроса о выборе теоретического закона для характеристики данного распределения. Приближенной же потому, что форма практической кривой распределения зависит не только от объективных причин – характера распределения размеров, но и от случайных – числа интервалов, количества принятых для анализа деталей N.
В связи с этим для объективной оценки точности обработки практическую кривую необходимо заменить теоретической кривой, изображающей вполне определенный закон распределения, описываемый математическим уравнением.
50 |
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
R, мм |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19,85 |
19,87 |
19,89 |
19,91 |
19,93 |
19,95 |
19,97 |
19,99 |
|
Рис. 5.3. Полигон распределения
По накопленным частотам (частостям) можно построить ку-
муляту или огиву.
Для построения кумуляты из верхней границы каждого интервала на оси абсцисс восстанавливаются перпендикуляры, соответствующие по высоте накопленной частоте mi или частости mi / N, с начала ряда по данный интервал, а затем последовательно плавно соединяют вершины. Полученная кривая называется кумулятой. Она отражает характер нарастания частот (частостей) от группы к группе.
Если оси поменять местами, то есть варианты откладывать на оси ординат, а накопленные частоты (частости) – на оси абсцисс, то построенная кривая называется огивой.
92
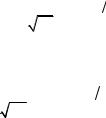
5.2.3.1. Теоретические законы распределения
Как уже указывалось, функции f (x), F(x), P(x) и λ(x) полностью характеризуют распределение случайной величины. Обычно эти функции задаются аналитическими выражениями (формулами). Существует несколько таких основных типов формул и соответствующих им типов распределений. В рамках одного типа распределения могут отличаться друг от друга параметрами. Параметр распределения – это исследуемый фактор, изменение которого определяет вид функции распределения. Параметр может быть одномерным или многомерным.
Для задания распределения случайной величины необходимо указать как тип, так и параметры распределения. Если у двух случайных величин совпадают и тип распределения, и параметры, то говорят, что они одинаково распределены. Рассмотрим основное распределение, наиболее часто встречающееся в теории надёжности.
5.2.3.2. Закон нормального распределения
Одним из наиболее распространенных законов распределения погрешностей является нормальное распределение Гаусса. График плотности кривой нормального распределения описывается зависимостью
y = f (x) = |
|
1 |
|
|
|
2 |
|
2 |
|
|
|
e− (xi − x ) |
2 |
|
|
||||||
|
|
|
σ |
. |
(5.1) |
|||||
σ |
2π |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Функция распределения имеет вид:
F (x) = |
|
1 |
x |
e−(xi − |
|
)2 2σ2 dx. |
|
|
x |
(5.2) |
|||||
σ |
|
||||||
|
2π –∞ |
|
|
|
|
||
График плотности нормального распределения называется нормальной кривой или кривой Гаусса (рис. 5.4). Закон Гаусса двухпараметрический и характеризуется следующими параметрами:
93
♦x – центр группирования, характеризует распределение размеров;
♦σ – характеризует кучность распределения размеров (погрешностей) около x ; чем меньше σ, тем кучнее распределяются размеры около x .
y
xmax
АB
xmin |
– 3σ |
|
+3σ |
|
|
ω = 6σ |
|
|
– σ |
σ |
x |
|
x |
|
|
Рис. 5.4. График плотности распределения Гаусса
Кривая Гаусса имеет следующие особенности:
1.Кривая симметрична относительно x .
2.При xi = x кривая имеет максимум:
y |
= |
|
1 |
≈ |
0,4 . |
|
σ |
2π |
|||||
max |
|
|
σ |
3. На расстоянии ± σ от вершины кривая имеет две точки перегиба А и В, координаты которых равны:
y |
|
= y |
|
= |
1 |
≈ 0,6y |
≈ |
0,24 . |
|
|
σ 2πe |
||||||
|
A |
|
B |
|
max |
|
σ |
4.На расстоянии ±3σ от вершины кривой её ветви так близки
коси абсцисс, что в пределах ±3σ 99,73 % всей площади ограничи-
ваются кривой. Практически принято считать, что на расстоянии
94

±3σ от вершины кривой ее ветви пересекаются с осью абсцисс, и в этих пределах заключена вся площадь кривой, то есть 100,0 %. Отклонение 3σ может считаться максимально возможным. Это положение называется правилом трех сигм. Погрешность в этом случае составляет 0,27 %, что допустимо при решении многих задач производства. В промежутке –σ…+σ заключаются 68,26 % всех значений параметров, между –2σ…+2σ – 95,44 %.
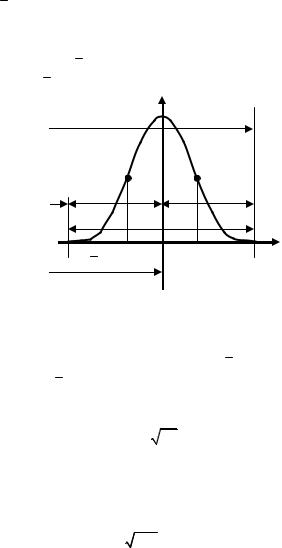
5. σ – это мера рассеяния, мера точности. При различных значениях средних квадратических отклонений кривые Гаусса представлены на рис. 5.5.
Рис. 5.5. Вид кривых нормальногораспределения случайных погрешностей приразличныхзначениях σ
На основаниип. 4 справедливоутверждение, что полерассеяния
ω ≈ 6 σ. |
(5.3) |
При определении σ по данным непосредственных измерений заготовок и расчётов по формуле (3.12) погрешность определения среднего квадратического, S, зависит от общего количества N измеренных заготовок. Следовательно, согласно формуле (5.4) и табл. 3.2 целесообразно принять соотношение:
σ = kσ S, |
(5.4) |
95

где kσ − коэффициент, учитывающий погрешность определения среднего квадратического (табл. 3.2); S – среднее квадратическое, определяемое по формуле (3.12).
В тех случаях, когда поле рассеяния параметров (размеров) превосходит поле допуска (ω > δ), условие обработки без брака не выполняется и брак является возможным.
Вероятный процент брака вычисляется следующим образом. При рассеянии размеров, соответствующих закону нормального распределения Гаусса, оценка точности принимается с погрешностью не более 0,27 %. Предполагается, что все действительные размеры партии деталей находятся в пределах поля рассеяния:
6 σ = xmax – xmin,
где xmax, xmin – максимальное и минимальное значения параметра (размера). При этом площадь, ограниченная кривой нормального распределения и осью абсцисс, равна единице и определяет 100 % заготовок партии. Выходящие по своим размерам детали за пределы допуска характеризуются как бракованные и отображены на рис. 5.6 площадями заштрихованных участков.
y
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
δ |
|
|
|
x |
xmin |
|
|
|
ω = 6σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
xmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 5.6. К определениюколичествагодныхдеталей
96

Тогда годные детали будут характеризоваться площадью, ограниченной кривой и осью абсцисс на длине, равной допуску δ. Для случая симметричного расположении поля рассеяния относительно поля допуска достаточно найти значение интервала, определяющего половину площади, ограниченной кривой Гаусса и абсциссой х1(х2).
Для случая, когда |
|
= 0, |
σ = 1 , распределение называют стан- |
||||
x |
|||||||
дартным и функция распределения (5.2) имеет |
следующий вид |
||||||
(рис. 5.7): |
|
|
|
|
|||
F(x) = |
|
1 |
x |
e− x2 2dx . |
(5.5) |
||
|
|
||||||
|
|
|
|
2π −∞ |
|
|
|
Вероятность появления случайной погрешности в этом случае определится площадью, ограниченной кривой f (x) и ее частью и осью абсцисс:
P{x1 < x < x2} = |
|
1 |
x2 |
|
|
|
x e− x |
2 2σ2 dx. |
(5.6) |
||
σ |
2π |
||||
|
|
1 |
|
|
|
Подынтегральное значение есть элемент вероятности, равный площади прямоугольника с основанием dx и абсциссами x1 и x2, на-
зываемыми квантилями.
Рис. 5.7. Функция распределения F(x) и функция Лапласа Ф(x)
97
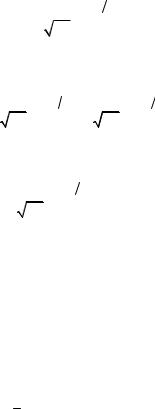
Произведя замену переменной: t = x / σ, dx = σ dt,
P{x < x < x |
} = |
|
|
1 |
t2 |
e−t2 2 dt , |
(5.7) |
|||||||||
|
|
|
t |
|||||||||||||
1 |
|
2 |
|
|
|
|
|
|
2π |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
представим правую часть (5.7) в виде суммы двух интегралов: |
||||||||||||||||
P{x < x < x |
} = |
1 |
|
0 |
e−t |
2 2dt + |
1 |
t2 |
e−t2 2dt . |
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
t |
2π 0 |
|||||||||||
1 |
2 |
|
2π |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Интеграл вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф(t) = |
|
|
1 |
|
|
t |
e−t2 2 dt |
|
(5.8) |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2π 0 |
|
|
|
|
|
|
||||
носит название нормальной функции Лапласа. Значения этого интеграла сведены в специальную таблицу [П11]. Таким образом, указанная вероятность (5.6) сводится к разности нормальных функций Лапласа:
Р{x1 < x < x2} = Ф(t2) – Ф(t1). |
(5.9) |
Для определения количества годных деталей необходимо определить величину t и Ф(t) [П11] с последующим пересчетом полученных величин в проценты или в число штук изделий.
В общем случае, когда x ≠ 0 , имеем следующую вероятность появления случайных погрешностей:
x2 |
|
|
|
|
|
|
|
|
|
|
|
x |
− x |
x |
− x |
|
|||||||
P{x1 ≤ x ≤ x2} = f (x) |
|
||||||||||
dx = Ф |
2 |
|
|
|
− Ф |
1 |
|
|
. |
(5.10) |
|
|
σ |
|
|
σ |
|
||||||
x1 |
|
|
|
|
|
|
|
|
|
||
Отметим свойства функции Лапласа: Ф(0) = 0; Ф(–х) = –Ф(х) (функция нечетная); Ф(∞) = 1/2. Из рис. 5.7 видно, что кривые F(х) и Ф(x) эквидистантны.
Если в равенстве (5.10) положить х1 = –∞, то
98
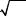
|
1 |
x2 |
− |
|
|
|
|
|
|
P(x ≤ x2 ) = |
x |
|
|
||||||
|
+ Ф |
|
|
|
|
|
, |
(5.11) |
|
2 |
|
σ |
|
|
|||||
|
|
|
|
|
|
|
|||
Поскольку Ф(–∞) = –Ф(∞) = –1/2. Положив в соотношении(5.10) х2 = ∞, находим:
|
1 |
x1 |
− |
|
|
|
|
|
P (x ≥ x1 ) = |
x |
|
||||||
|
− Ф |
|
|
|
|
. |
(5.12) |
|
2 |
|
σ |
|
|
||||
|
|
|
|
|
|
|||
При построении теоретической кривой по эмпирическим данным используют следующую формулу для нахождения теоретических частот:
|
n |
|
|
|
|
|
|
|
|
mi′ = |
h mi |
|
1 |
e- |
t2 |
|
|||
i=1 |
|
2 |
, |
||||||
σ |
|
|
2π |
||||||
|
|
|
|
|
|
|
|||
где h – величина интервала, t = (xi – |
|
|
|
)/σ. |
|
|
|||
|
x |
|
|
||||||
В технических требованиях введен индекс, связывающий изменчивость реального процесса с полем допуска, называемый индексом воспроизводимости «Ср»:
Ср = δ/6σ.
Для описания возможности нецентрированного процесса используется индекс «Cpk». Для упрощения расчёта долго- и краткосрочной изменчивости и определения вариации вокруг установленного целевого значения существуют и используют другие индексы.
Использование анализа возможностей процесса для определения способности процесса производить продукцию, соответствующую установленным требованиям, и оценки ожидаемого количества несоответствующей продукции позволяет поставщику оценить издержки от несоответствий и помогает принять решения по улучшению процесса.
Установление минимального значения на индекс возможностей процесса помогает поставщику в выборе процессов и оборудования, способных производить продукцию необходимого качества.
99

Двумерным нормальным распределением называют распределение вероятностей двумерной непрерывной случайной величины (X, Y), если функция плотности имеет вид:
|
|
|
|
|
f (X ,Y ) = |
|
1 |
|
|
|
× |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2πσ1σ2 1 |
− ρ2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
(x − x) |
|
( y − y) |
|
|
(x − x)( y − y) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
× exp − |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− 2ρ |
|
|
|
|
|
. |
|
2(1− |
ρ |
2 |
) |
2 |
|
|
|
2 |
|
|
|
σ1σ2 |
|||||||||||
|
|
|
σ1 |
|
|
|
σ2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.1. При измерении сопротивлений делителя напряжения установлено, что среднее значение этого сопротивления R = 5,5 кОм, а среднее квадратическое отклонение σ = 1,5 кОм. Принимая нормальный закон распределения, найти вероятность появления сопротивлений свыше 10 кОм.
Решение. По равенству (1.36) и из таблицы [П11] находим:
Р(R > 10) = 1/2 – Ф[(10 – 5,5)/1,5] = 0,5 – 0,4986 = 0,0014.
Пример 5.2. Определить количество бракованных и годных деталей, если допуск на обработку δ = 0,10 мм. Среднее квадратическое отклонение S = 0,02 (получено по результатам замеров 75 шт.). Общее количество обработанных деталей – 300 шт.
Решение:
1.Определяемрасчётноезначениеσ= kσ S = 1,25 0,02 = 0,025 мм.
2.Поле фактического рассеяния ω = 6σ = 6 0,025 = 0,15 мм превосходит поле допуска δ = 0,1 мм; следовательно, условие обработки без брака не выполнено ипоявление бракавозможно.
3.x = δ/2 = 0,1/2 = 0,05; t = x/σ = 0,05/0,025 = 2,0. Ф(t) = 0,4772,
что соответствует 47,72 % годных деталей для половины партии. Для всей партии количество годных деталей – 95,44 % или 286 шт., а бракованных – 4,56 % или 14 шт.
Метод оценки точности на основе кривых распределения универсален и позволяет объективно оценить точность механической
100
