
Статистические исследования контроля качества в автоматизированных
..pdfгоугольнике распределения мода − это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.
Коэффициент вариации случайной величины − это относительная мера вариации.
V(X) = |σ(X) / Mх(X) |·100 %.
Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) Sk(X) − величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии дискретной случайной величины вычисляется по формуле
Sk(X) = [(x1 – Mх(X))3Р1 + (x2 – Mх(X))3Р2 + … + + (xn – Mх(X))3Рn]/σ3.
Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находится левее математического ожидания, и наоборот, если Sk(X) > 0, то правее.
Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ek(X) − величина, характеризующая степень островершинности или плосковершинности распределения, то есть степень так называемого «выпада». Коэффициент эксцесса дискретной случайной величины вычисляется по формуле
Ek(X) = [(x1 – Mх(X))4Р1 + (x2 – Mх(X))4Р2 + … + + (xn – Mх(X))4Рn]/σ4 – 3.
Пример 3.1. Составить закон распределения случайной дискретной величины X, которая может принимать 5 значений. Найти:
♦её числовые характеристики;
♦функцию распределения;
♦вероятность того, что X примет значение меньше Mх;
♦вероятность того, что X примет значение больше 0,5 Mх.
21

Решение. Закон распределения дискретной случайной величины X – это перечень всех возможных значений случайной величины X, которые она может принимать, и соответствующих вероятностей. Сумма всех вероятностей должна равняться 1.
Проверка: Р = 0,1 + 0,2 + 0,5 + 0,1 + 0,1 = 1.
Значения распределения случайной величины Х
xi |
–2 |
–1 |
Pi |
0,1 |
0,2 |
0 |
1 |
2 |
|
|
|
0,5 |
0,1 |
0,1 |
|
|
|
Построим многоугольник распределения (рис. 3.1).
Рис. 3.1. Многоугольник распределения случайной величины Х
Математическое ожидание
Mх(X) = –2 · 0,1 – 1 · 0,2 + 0 · 0,5 + 1 · 0,1 + 2 · 0,1 = –0,1.
Дисперсия – это математическое ожидание квадрата отклонений значений случайной величины X от её математического ожидания:
D(X) = (–2 + 0,1)2 · 0,1 + (–1 + 0,1)2 · 0,2 +
+(0 + 0,1)2 · 0,5 + (1 + 0,1)2 · 0,1 + (2 + 0,1)2 · 0,1 = 1,09
или
22
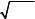
D(X) = (–2)2 · 0,1 + (–1)2 · 0,2 + 02 · 0,5 + 12 · 0,1 + + 22 · 0,1 – (–0,1)2 = 1,1 – 0,01 = 1,09.
Среднее квадратическое отклонение – это корень квадратный из дисперсии,
σ = 1,09 ≈ 1,044.
Коэффициент вариации V(X) = [1,044/0,1] · 100 % = 1044 %.
Коэффициент асимметрии
Sk(X) = [(–2 + 0,1)3 · 0,1 + (–1 + 0,1)3 · 0,2 + (0 + 0,1)3 · 0,5 + + (1 + 0,1)3 · 0,1 + (2 + 0,1)3 · 0,1]/1,0443 = 0,200353.
Коэффициент эксцесса
Ek(X) = [(–2 + 0,1)4 · 0,1 + (–1 + 0,1)4 · 0,2 + (0 + 0,1)4 · 0,5 + + (1 + 0,1)4 · 0,1 + (2 + 0,1)4 · 0,1]/1,0444 – 3 = 0,200353.
0 |
при |
x ≤ −2, |
|
при − 2 < x ≤ −1, |
|
0,1 |
||
0,3 |
при − 1< x ≤ 0, |
|
F(X ) = |
при |
0 < x ≤ 1, |
0,8 |
||
0,9 |
при 1 < x ≤ 2, |
|
|
при |
x > 2. |
1,0 |
||
|
|
|
Функция распределения – это вероятность того, что случайная величина X примет значение меньшее, чем какое-либо числовое значение x:
F(X) = P(X < x).
Значения определяем суммированием вероятностей. Функция распределения – функция неубывающая. Она принимает значения в интервале от 0 до 1.
23
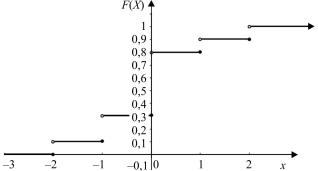
Рис. 3.2. График дискретной функции распределения
P(X < – 0,1) = F(–0,1) = 0,3.
P(X > – 0,05) = P(0) + P(1) + P(2) = 0,5 + 0,1 + 0,1 = 0,7.
График функции распределения представлен на рис. 3.2.
3.2. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Непрерывными одномерными случайными величинами называют такие, которые в некотором интервале могут принимать любое значение из конечного или бесконечного интервала.
В генеральной совокупности дискретной случайной величиной будет число бракованных изделий в различных выборках, а непрерывной случайной величиной – размер этих изделий.
Разбивая все возможные значения непрерывной случайной величины на интервалы и задавая вероятности появления этих интервалов, можно задать ее в виде дискретной. Случайные величины характеризуются функциями распределения вероятностей.
Кроме случайной на практике приходится иметь дело и с сис-
тематической величиной. Систематическая погрешность производ-
ства продукции является составляющей из всей совокупности погрешностей производства продукции. При неизменных условиях
24
производства она сохраняет или принимает закономерно изменяющийся модуль и (или) знак. Систематическая погрешность остается постоянной или закономерно изменяется при повторных измерениях одного и того же физического параметра. Она может возникнуть, например, из-за неправильного монтажа устройства или из-за постоянного внешнего воздействия (нагрев, вибрация и т. д.). Систематическая величина может быть исключена путем введения поправки, равной по величине и обратной по знаку погрешности.
3.3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
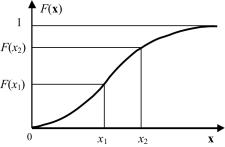
Распределение случайной величины – функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу. Если X – случайная величина, а x – некоторое ее значение, то вероятность Р того, что случайная величина X не превысит значения x, то есть попадет в интервал (−∞, x):
F(x) = P(X < x),
где F(x) – интегральная функция распределения (рис. 3.3), определяющая для всех действительных х вероятность того, что случайная величина Х принимает значения, не больше, чем х.
Рис. 3.3. Интегральная функция распределения
25
Ее задание и определяет закон распределения случайной величины Х. В общем случае функция распределения F (x) может быть как разрывной, так и непрерывной.
Распределение многомерной случайной величины – функция, которая однозначно определяет вероятность того, что случайные величины (Х1, Х2, …, Хn) принимают значения (х1, х2, …, хn) или вероятность того, что каждая из случайных величин находится в определенном интервале:
P(X1 = x1, …, Xn = xn). P(a1 < Х1 < b1, …, an < Xn < bn).
С точки зрения практических исследований распределение недискретных случайных величин целесообразно задавать с помо-
щью введения функции плотности вероятностей f (x).
Для случайной величины характерно то, что заранее не известно, какое из значений она примет. Количественно оценивать возможность случайной величины Х принимать значения в интервале (х1, х2) можно вероятностью
P(x1 < X ≤ x2) = f (x) dx, |
(3.1) |
где P(x1 < X ≤ x2) – вероятность указанного события |
(x1 < X ≤ x2); |
f (x) − плотность распределения случайной величины; x2 = x1 + dx. Плотность f (x) – первая производная (если она существует)
функции распределения. Плотность является важнейшей характеристикой, задающей распределение случайной величины. Плотность удовлетворяет двум условиям: она неотрицательна и интеграл от нее в полных пределах изменения аргумента х равен единице:
∞ |
|
|
f (x) ≥ 0; |
f (x) dx = 1 . |
(3.2) |
−∞ |
|
|
Как видно из формул (3.1) и (3.2), функция распределения |
||
F(х) выражается через плотность f (х): |
|
|
F (x) = x |
f (x)dx . |
(3.3) |
−∞ |
|
|
26
С другой стороны, если плотность f (х) непрерывна в точке х, то ее значение в этой точке равно производной от функции F (х):
f (x) = F′(x). |
(3.4) |
Согласно предположению (3.4) функция распределения F (x) будет являться первообразной для плотности f (x):
x2
P(x1 < x < x2 ) = f (x) dx = F (x) = F (x2 ) − F (x1 ).
x1
Функцию f (x) называют также дифференциальной функцией распределения.
Из свойств плотности f (x) и определения функции F (x) следует, что последняя – неотрицательна, не убывает и равна 0 и 1 при значении аргумента –∞ и ∞:
F (x) ≥0; F (х1) ≥ F (х2) при x1 > х2; F (– ∞ ) = 0; F ( ∞ ) = 1.
График плотности распределения f (x) называется кривой распределения случайной величины. Геометрическая интерпретация интеграла, как площадь соответствующей криволинейной трапеции, показывает, что для произвольного числа, находящегося в интервале х0 – ∞ < х0 < ∞, число F (x0) равно площади под кривой распределения, лежащей левее прямой х = х0. Аналогично интерпретируется вероятность P (x1< x ≤ x2) (рис. 3.4).
Случайная величина X, для которой существует плотность распределения f (x), называется непрерывной.
Случайная величина может быть многомерной – совокупно-
стью одномерных случайных величин, являющихся координатами случайной точки в многомерном пространстве. Многомерная случайная величина может быть непрерывной или дискретной в зависимости от того, являются ли все члены последовательности непрерывными или дискретными.
27
y
y = f(x)
F(x0) |
P(x1<x<x2) |
|
x0 |
0 |
x1 |
x2 |
x |
|
Рис. 3.4. Плотность распределения случайной величины
Функция распределения многомерной случайной величины F(x1, x2, …, xn) – функция, определяющая для всех действительных x1, x2, …, xn вероятность того, что одновременно случайная величина X1 принимает значение не больше, чем x1, случайная величина X2 принимает значение не больше, чем x2, …, случайная величина Xn принимает значение не больше, чем xn:
F(x1, x2, …, xn) = P(X1 ≤ x1, X2 ≤ x2, …, Xn ≤ xn).
Плотность вероятности многомерной случайной величины f (x1, x2, …, xn) – функция (если она существует), являющаяся n-й смешанной частной производной функций распределения:
f (x |
,..., x )= |
∂n F(x ,..., x ) |
. |
|
1 |
n |
|||
1 |
n |
∂x1...∂xn |
|
|
|
|
|
|
|
Произведение f (х) dх определяет вероятность отказа объекта в интервале времени (х1, х2), если под случайной величиной X понимать продолжительность безотказной работы объекта. Вероятность отказа объекта до момента х будет определять значение функции распределения F(х). В теории надежности часто употребляют такое понятие, как вероятность безотказной работы Р(х),
28
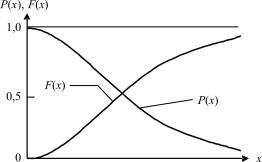
которое является дополнительным понятием к функции распределения F(x).
Значение вероятности безотказной работы в точке х равно вероятности того, что случайная величина X превысит х, то есть изделие будет работать безотказно в течение времени x:
Р(х) = 1 – F(х) = P{X > х}.
Функция Р(х) называется также функцией надежности. Примерные графики функции распределения F(х) и функции надежности Р(х) изображены на рис. 3.5.
Рис. 3.5. Графики функции распределения F(x) и функции надежности Р(х)
На практике часто располагают дополнительной информацией о том, что случайная величина превысила некоторое значение х (в частности, это изделие проработало время x и не отказало).
Разумеется, эта информация изменяет возможность принятия случайной величиной тех или иных значений. В связи с этим вводят специальную функцию − интенсивность отказов λ(х). Значение интенсивности отказов в точке х, умноженное на dх, равно вероятности принятия случайной величиной значения из элементарного интервала (х1, х2) при условии, что эта случайная величина X больше х:
29
λ(х)dx = P{x < x ≤ x + dx | X > x},
где символ «|» означает «при условии, что…».
В нашем контексте λ(х)dx есть вероятность отказа изделия сразу после момента времени х, если оно до этого не отказало.
3.4. МЕРЫ ПОЛОЖЕНИЯ И РАССЕЯНИЯ КРИВОЙ РАСПРЕДЕЛЕНИЯ
Мера положения на оси абсцисс и рассеивание характеризуют кривую распределения плотностей вероятностей случайной величины. В этом случае средняя арифметическая является основной, характеризующей центр группирования. Однако на практике при статистическом исследовании случайных величин особое место занимает изучение их вариации и характера распределения по изучаемому признаку.
Для оценки положения и рассеяния кривой распределения вводятся соответствующие критерии или меры.
Кмерам положения относятся мода, математическое ожидание и медиана случайной величины.
Кмерам рассеяния относятся стандартное отклонение, дисперсия и размах.
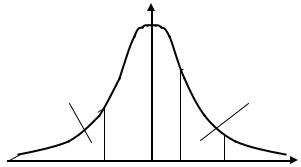
Функция распределения плотности вероятностей может иметь одно или несколько максимальных значений в разных местах области (рис. 3.6). Значения случайной величины, соответствующие локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины, называются модой распределения (Mо).
Мода для дискретного ряда определяется как вариант, имеющий наибольшую частоту или частость.
Для интервального ряда с равными интервалами мода рассчитывается по формуле
30
