
то что давала филимонова / Лекции Механика для студентов Физика
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
(ГОУ ВПО ИГУ)
КАФЕДРА ОБЩЕЙ ФИЗИКИ
КУРС ЛЕКЦИЙ
МЕХАНИКА
для специальности: |
010400 |
физика |
ИРКУТСК 2005 г
1
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
СОДЕРЖАНИЕ
№ |
Название лекции |
Стр. |
|
1 |
Скалярные и векторные величины, действия над ними. |
4 |
|
Вычисление компонент вектора. |
|||
|
|
||
2 |
Перемещение и скорость в векторной и координатной |
6 |
|
формах. |
|||
|
|
||
3 |
Ускорение векторной и координатной формах. |
8 |
|
4 |
Преобразование декартовых координат и компонент |
12 |
|
вектора. Инвариантный характер вектора. |
|||
|
|
||
5 |
Нерелятивистская и релятивистская механика. |
14 |
|
Постулаты Эйнштейна. |
|||
|
|
||
6 |
Относительность одновременности и принцип |
19 |
|
причинности. Сокращение длины и изменение формы |
|||
|
движущихся тел. |
|
|
|
Длительность событий, собственное время, |
|
|
7 |
замедление хода движущихся часов. 3-е следствие |
21 |
|
|
преобразований Лоренца. |
|
|
8 |
Сложение скоростей по Лоренцу. Законы Ньютона. |
24 |
|
Невыполнение 3-о закона Ньютона. |
|||
|
|
||
|
Продольная и поперечная масса. Релятивистское |
|
|
9 |
уравнение движения. Момент силы, момент импульса |
28 |
|
|
силы. Уравнение моментов для материального тела. |
|
|
|
Основные механические параметры системы |
|
|
10 |
материальных частиц. Центр масс. Теорема о |
30 |
|
движении центра масс. Закон сохранения импульса |
|||
|
|
||
|
для системы материальных тел. |
|
|
11 |
Работа, мощность, потенциальная энергия, градиент |
33 |
|
потенциальной энергии. |
|||
|
|
||
|
Кинетическая энергия, закон сохранения энергии |
|
|
12 |
(нерелятивистский случай). Графическое |
37 |
|
|
представление энергии. |
|
|
13 |
Законы Кеплера |
40 |
|
14 |
Закон сохранения энергии (релятивистский случай). |
42 |
|
Закон взаимодействия массы и энергии. |
|||
|
|
||
|
Столкновения. Их виды. Упругие столкновения. |
|
|
15 |
Векторная диаграмма. Лобовые столкновения. |
50 |
|
|
Неупругие столкновения. |
|
|
16 |
Поле вблизи поверхности Земли. Гравитационная |
68 |
|
энергия тел. Движение в поле тяготения. |
|||
|
|
||
17 |
Динамика тел переменной массы. |
85 |
|
18 |
Космические скорости. Движение искусственных |
98 |
|
спутников Земли. |
|||
|
|
||
19 |
Неинерциальные системы отсчёта. |
109 |
2
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
20 |
Колебания. Гармонические и собственные колебания. |
130 |
|
21 |
Затухающие и вынужденные колебания. |
145 |
|
22 |
Автоколебания, параметрические колебания и |
167 |
|
колебания связанных систем. |
|||
|
|
||
23 |
Волновое движение. Бегущие и стоячие волны. |
179 |
|
Интерференция и дифракция волн. |
|||
|
|
||
24 |
Движение твёрдого тела. Гироскопы. |
214 |
|
25 |
Деформация в твердых телах. Виды деформаций. |
243 |
|
Закон Гука. Энергия упругих деформаций. |
|||
|
|
||
26 |
Упругие напряжения. Модули Юнга и сдвига. Энергия |
254 |
|
упругих деформаций. |
|||
|
|
||
|
Жидкость и газ в состоянии равновесия. Условия |
|
|
27 |
равновесия. Законы Паскаля. Распределение давлений |
260 |
|
в жидкости, находящейся во внешнем поле. Плавание |
|||
|
|
||
|
тел. |
|
|
|
Список литературы |
271 |
3
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ, ДЕЙСТВИЯ НАД НИМИ. ВЫЧИСЛЕНИЕ КОМПОНЕНТ ВЕКТОРА.
Все физические величины делятся на два класса: скалярные и векторные.
Скалярные величины – величины для характеристики которых необходимо знать только их численное значение (S - путь, m, t, A, P - мощность) Векторные величины – величины для характеристики которых необходимо знать не только их численное значение, но и направление. Векторы характеризуются точкой приложения, направлением и модулем (длиной). Векторы можно складывать, вычитать, а так же скалярно и векторно умножать.
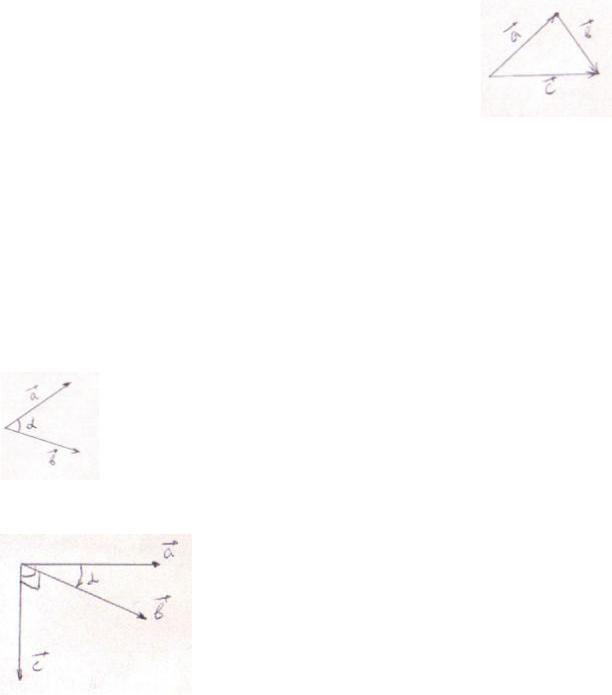
Сложение векторов: A + B = C
1.Правило треугольника: Используя параллельный перенос поместим начало B в конец A . Соединим начало A и конец B вектором С, с началом в начале вектора А и концом в конце вектора В.
2.Правило параллелограмма: Используя
параллельный перенос совместим начала векторов
А и В. Проведем из конца вектора А прямую AO
 B и прямую BO
B и прямую BO
 A .
A .
Тогда начало результирующего вектора С будет совпадать с началами векторов А и В, а конец будет лежать в точке О.
Вычитании векторов производится аналогично сложению, однако сначала у вычитаемого вектора следует изменить направление на противоположное.
Умножение вектора на число: A× R = B
Результатом умножения вектора А на число является вектор В, направление
которого совпадает с направлением вектора А, а |
r |
< |
r |
в R раз. |
A |
B |
|||
|
|
|
|
|
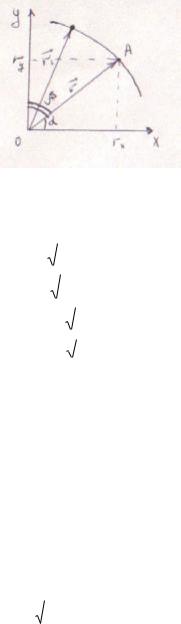
Скалярное умножение векторов: A× B = C
Результатом скалярного умножения векторов является число (скаляр), равный произведению модулей умножаемых векторов
на косинус угла между ними. C = |
r |
× |
|
r |
× cos(α) |
|
|
A |
B |
|
|||||
Векторное |
умножение |
векторов: |
A´ B = C или |
||||
[A× B] = C |
|
|
|
|
|
|
|
Результатом |
векторного |
|
произведения векторов |
||||
является |
вектор, |
лежащий в |
плоскости, |
||||
перпендикулярной плоскости, в которой лежат
перемножаемые вектора и равный по модулю произведению модулей векторов на синус угла
4
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
между ними. Направление результирующего вектора определяется по правилу «Буравчика» и совпадает с поступательным направлением движения
при вращении от первого из перемножаемых векторов ко второму по кратчайшему пути (наименьшему углу).
Сложение векторов, а так же их скалярное умножение обладает свойством коммутативности. Т. е. при перестановке векторов результат не меняется.
Компоненты векторных величин:
|
OX |
|
= |
|
r |
× cosα = x = rx |
||
|
|
|
r |
|||||
|
OY |
|
|
= |
|
r |
|
×sinα = y = ry |
|
|
|
r |
|
||||
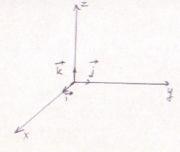
Точка А характеризуется координатой. Каждая точка в кинематике характеризуется радиус-вектором r .
Радиус-вектор – вектор, проведенный из начала
координат к любой точке траектории в любой
момент времени. Если t=0, тогда r = r .
r r0
x,rx - проекция материальной точки на ось ОХ. y, ry - проекция материальной точки на ось OY.
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
= |
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
|
= r2 |
+ r2 |
|
|
|
|
|
|
|
|
|
||||||||
|
r |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
= r × |
cos2 α + cos2 β |
|
|
|
|
||||||||||||
r |
|
|
|
|
|
|||||||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) |
= r × |
sin2 α + cos2 α |
|
|
|
|
||||||||||||||
r |
|
|
|
|
||||||||||||||||
r |
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
||
r |
= rx |
+ ry |
|
|
|
|
|
|
|
|
|
|
|
|||||||
На |
рисунке |
rx и ry |
- |
|
проекции |
радиус-вектора на соответствующие оси |
||||||||||||||
(скалярные величины). |
|
|
,ry ,rz используют единичные орты для оси |
|||||||||||||||||
Для определения направлений rx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r r |
ОХ - |
|
|
r |
|
|
r |
|
|
r |
|
||||||||||
i = ex , OY - |
j = ey |
, OZ - k = ez |
|
|||||||||||||||||
r |
|
|
|
|
|
r |
× cosα = i × r |
|
|
|
|
|
|
|
|
|||||
r |
= r |
|
|
|
|
|
|
|
|
|||||||||||
rx |
|
|
|
|
|
r |
|
|
|
r |
x |
|
|
|
|
|
|
|
|
|
ry |
|
= r |
×sinα = j |
× ry |
r = ex |
× x + ey × y + ez × z . |
||||||||||||||
Таким образом: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
r |
r |
|
|
Векторные величины могут быть записаны через компоненты.
r |
|
|
|
|
|
|
|
= |
|
|
r2 |
+ r2 |
+ r2 |
||
r |
|
|
|||||
|
|
r |
|
x |
y |
z |
|
rx |
|
|
r |
= 1× r × cosα |
|||
= i |
× r |
||||||
ry |
= |
r |
|
r |
|
|
|
j |
× r |
|
|
|
|||
rz |
|
r |
|
r |
|
|
|
= k |
× r |
|
|
|
|||
Проекция вектора равна скалярному произведению орты соответствующей оси на вектор.
1. Скалярное произведение орт:
5
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
i × i = j × j = k × k |
= 1 |
||||||
r |
r |
r |
r |
= |
r |
r |
= 0 |
i |
× j |
= i |
× k |
j |
× k |
||
При скалярном перемножении одноименных орт получаем 1, а разноименных
–0.
2.Векторное произведение орт:
ir ´ ir = 0 |
i ´ j = k |
||||
r |
r |
= 0 |
r |
r |
r |
j |
´ j |
k ´ i |
= j |
||
r |
r |
= 0 |
r |
r |
r |
k |
´ k |
j ´ k |
= i |
||
j ´ i = -k
r |
r |
r |
i |
´ k |
= -j |
r |
r |
r |
k ´ j = -i
|
|
|
|
Действия над векторами, выраженными в |
|
|
|
|
координатной форме: |
|
|
|
|
1. Сложение: |
r |
+ b |
= i × ax + j × ay + k × az + i ×bx + j ×by + k ×bz = i × (ax + bx ) + j × (ay + by ) + k × (az + bz ) = |
||
a |
||||
r |
r |
r |
r |
× cz |
c |
= i |
× cx + j |
× cy + k |
|
Компоненты результирующего вектора равны сумме соответствующих компонент слагаемых.
|
2. |
Скалярное умножение: |
|
Перемножим векторы, используя скалярное произведение орт. |
|||
r |
×b = (i × ax + j × ay + k × az ) × (i ×bx + j ×by + k ×bz ) = ax ×bx + ay ×by + az ×bz |
||
a |
|||
r |
3. |
Векторное умножение: |
|
´ b |
= (i × ax + j × ay + k × az ) ´ (i ×bx + j ×by + k ×bz ) = i × (aybz - azby ) + j × (azbx - axbz ) |
||
a |
|||
|
r |
|
|
+ k × (axby - aybx ) |
|||
|
ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ В ВЕКТОРНОЙ И КООРДИНАТНОЙ |
||
|
ФОРМАХ ДЛЯ СЛУЧАЯ, КОГДА r = r (t) (ДВИЖЕНИЕ ЗАДАНО ЧЕРЕЗ |
||
|
ПАРАМЕТРЫ r ) И r = r(s) (ДВИЖЕНИЕ ЗАДАНО ЧЕРЕЗ ПАРАМЕТРЫ |
||
|
|
ТРАЕКТОРИИ). |
|
Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел.
Траектория – линия, которую описывает материальная точка при своем движении.
Путь – длина траектории.
Перемещение – вектор, проведенный из точки начального положения частицы в точку конечного.
6
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Система координат – совокупность базисных векторов, с началом в заданной точке.
Система отсчета.
rt 2 - rt1 = r2 - r1 = Dr - перемещение т. е. Перемещение – приращение радиус- вектора.
r |
r |
|
r |
|
r |
− r |
- вектор средней |
|
vср =< v |
>= |
|
= |
|
2 |
1 |
||
Dt |
t |
2 |
- t |
|||||
|
|
|
|
|
|
1 |
|
|
скорости.
Вектор средней скорости показывает изменение перемещения в единицу времени (он всегда направлен по линии
перемещения). Пусть t → 0 тогда:
r |
dr |
r |
r |
′ |
|
limvср = |
|
= v |
= rt |
||
dt |
|||||
|
|
|
|
Где v - вектор мгновенной скорости. Вектор мгновенной скорости направлен по касательной к траектории и равен первой производной радиус-вектора по времени.
(Процесс предельного перехода, с помощью которого определяется производная функции называется дифференцированием.)
r |
r |
r |
|
dx |
r |
|
dy |
r |
|
dz |
|
dx |
|
dy |
|
dz |
, гдеvx ,vy ,vz |
- проекции |
|
v |
= rt |
¢= i |
× |
|
+ j |
× |
|
+ k |
× |
|
Þ vx = |
|
, vy = |
|
, vz = |
|
|||
dt |
dt |
dt |
dt |
dt |
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
мгновенной скорости на соответствующие оси.
Путевая скорость.
1) Средняя скорость прохождения пути:
< v >= vср = Dst
2) Мгновенная путевая скорость:
vs = dsdt = st¢
Т. к. S – путь – скалярная величина,
то модуль мгновенной путевой скорости представляет собой абсолютную скорость движения.
vабс = vs
Рассмотрим случай, когда r зависит не от t, а от S, т. е. значение,
7
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
заданного через параметры траектории r , является сложной функцией.
r |
|
dr (S) |
r |
|
dr |
|
dS |
|
dr |
|
|||
v = |
|
|
|
|
v |
= |
|
× |
|
= |
|
× vабс |
|
|
dt |
|
|
dS |
dt |
dS |
|||||||
r |
|
|
|
|
|
|
|
|
|||||
|
r |
|
r |
|
r |
|
r |
|
|
|
|
||
dr |
|
|
|
|
|
|
|
|
|||||
|
|
= rs¢ |
= τ Þ v |
= τ × vабс |
|
|
|||||||
dS |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
τ характеризует быстроту изменения направления перемещения в расчете на единицу длины траектории (τ - быстрота поворота вектора перемещения, единичный вектор, направленный по касательной к траектории).
t |
|
r |
|
t |
|
r |
|
r |
r |
r |
r |
r |
|
|
2 |
dr |
|
|
2 |
|
|||||||
ò |
|
× dt |
= òv |
× dt |
= rt2 |
- rt1 |
= v(t2 |
- t1) = r2 |
- r1 |
||||
dt |
|||||||||||||
t |
1 |
|
t |
1 |
|
r |
r |
r |
|
|
|
||
|
|
|
|
|
|
|
|
||||||
Пусть t1 |
|
|
|
×t2 |
|
|
|||||||
= 0 Þ r2 |
- r0 |
= v |
|
|
|||||||||
УСКОРЕНИЕ В ВЕКТОРНОЙ И КООРДИНАТНОЙ ФОРМАХ.
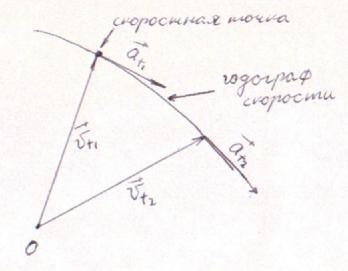
Рассмотрим годограф скорости:
r |
r |
v |
- вектор |
1) < a |
>= aср = |
t |
|
|
|
|
среднего ускорения характеризует изменение вектора скорости в единицу времени.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
dv |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
a |
= |
|
= |
rt′′ |
- |
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мгновенного |
ускорения |
равен |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производной |
|
от |
вектора |
||||
времени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мгновенной |
|
скорости |
по |
|||||||||
r |
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
r |
|
|
|
|
|
dvx × i + dvy |
× j + dvz × k |
|
r |
|
r |
|
|
r |
|
|
|
||||||||||
|
|
|
|
dv |
|
|
|
|
|
|
|
|
||||||||||||||||
3) a = |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= i |
× ax + j |
× ay + k |
× az |
|
|
|||||||
|
dt |
|
dvy |
|
dt |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4) ax = |
|
dv |
x |
|
|
ay = |
az = |
dv |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
dt |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
r |
|
|
|
|
r |
|
r |
|
|
r |
|
|
r |
|
|
r |
|
|
r |
|
|
r |
|
|
|
||
|
d 2r |
|
|
|
|
|
¢¢ |
|
|
¢¢ |
¢¢ |
¢¢ |
|
|
||||||||||||||
|
a = |
|
|
|
|
|
|
|
= (i × x + |
|
|
|
|
= i |
|
|
|
|
|
|||||||||
5) |
dt 2 |
j × y + k × z)t |
× xt |
+ j × yt + k × zt |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6) Сравнивая 5) и 3) получаем: ax = xt′′ |
ay = yt′′ |
az = zt′′ где |
ax ,ay ,az - |
|||||||||||||||||||||||||
проекции вектора ускорения на соответствующие оси. |
|
|
|
|
|
|||||||||||||||||||||||
Годограф позволяет упрощать решение задач, если линейная скорость равна
ω * R .
8
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

a = ω × v = ω 2 × R = an
Линейная скорость – зависимость изменения координаты от времени.
Рассмотрим поступательное и вращательное движение: при этом скорость тела характеризуется не только линейной, но и угловой скоростью, а так же нормальным (центростремительным) и тангенциальным ускорением. Линейная скорость меняет свой модуль и направление. Нормальное ускорение зависит от скорости изменения направления движения.
an - изменение линейной скорости по направлению в единицу времени; направлена по радиусу к центру окружности.
n |
- единичный |
|
вектор, направленный в ту же сторону, что и вектор |
|||
нормального ускорения. |
||||||
r |
r |
|
v2 |
r |
2 |
|
an = n |
× |
|
= n ×ω |
|
× R |
|
R |
|
|||||
|
|
|
|
|
|
|
aτ - изменение модуля линейной скорости в единицу времени.
|
|
|
d |
r |
|
|
dv |
|
r |
r |
dv |
|
|
|
|||
|
|
|
v |
|
|
|
|
|
|
||||||||
aτ |
= |
|
|
|
= |
|
; |
aτ = τ × |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
dt |
|
dt |
dt |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
|
|
|
|
|
|
|
|
æ dv ö2 |
æ v2 |
ö2 |
|||||
|
|
|
|
2 |
|
2 |
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
a |
= |
aτ + an |
= |
|
|
|
|
|
ç |
|
÷ |
|||||
|
ç ÷ |
|
|||||||||||||||
|
+ ç |
|
÷ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
è dt ø |
è |
R |
ø |
||||
Тангенциальное ускорение сонаправленно со скоростью, если тело движется ускоренно и направленно в противоположную сторону, если тело движется
замедленно. |
aτ |
|
|
всегда направленно по касательной к траектории. |
||||||||||||||||||||||||||
Ориентация ускорения относительно траектории: |
||||||||||||||||||||||||||||||
r = r (S ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
|
|
r |
|
|
d |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
= |
|
|
= |
|
|
|
(τ (S )×v) |
|
|
|
|
|
|
|
|
||||||||||||||
dt |
|
dt |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
= τ (S )×v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
r |
|
|
dτr(S ) |
|
|
|
r |
dv |
|
|
|
|
|
|
|
|
|||||||||||||
a |
= |
|
|
|
|
|
×v +τ × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dτr(S ) |
|
dτr(S ) |
|
dS |
|
|
|
|
dτr |
|
r |
|
2 |
|
dτr |
r |
|||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
× |
|
|
|
= v × |
|
|
Þ a |
= v |
|
× |
|
+τ × aτ |
|||||
|
|
dt |
|
|
|
|
|
dS |
|
dt |
|
dS |
|
dS |
||||||||||||||||
Найдем угол между |
dτ |
иτr : |
|
|
|
|
|
|||||||||||||||||||||||
dS |
|
|
|
|
|
|||||||||||||||||||||||||
|
dτ |
r |
|
|
|
|
|
d(τ ,τ ) |
|
|
|
|
|
|
|
dτ |
|
|
|
|
|
|||||||||
|
|
×τ = 0.5 × |
|
|
|
|
= 0.5 × 2 ×τ × |
|
|
|
|
|
|
|
||||||||||||||||
|
dS |
|
dS |
|
|
dS |
|
|
|
|
|
|||||||||||||||||||
9
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
Т. к. |
|
r |
|
|
|
|
|
|
dτ |
|
|
|
dτ |
|
r |
Þ он направлен по радиусу кривизны. |
||||||||
|
τ |
|
= τ = const Þ |
|
|
= 0 Þ |
|
^ v |
||||||||||||||||
|
|
dS |
dS |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
dτ |
|
|
- вектор характеризующий быстроту поворота касательной к траектории |
||||||||||||||||||||
|
dS |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
движения в расчете на единицу длины траектории. |
||||||||||||||||||||||||
|
dτr |
|
|
= k = |
1 |
- кривизна траектории |
|
|||||||||||||||||
|
|
|
||||||||||||||||||||||
|
dS |
R |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dτ |
|
|
|
|
r |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= n × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dS |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
r |
|
|
r |
1 |
|
|
|
2 |
r |
|
v2 |
dv |
|
||||||||||
a = n |
× |
|
× v |
|
+τ × aτ Þ an = |
|
|
,aτ = |
|
|
|
|||||||||||||
R |
|
R |
dt |
|
||||||||||||||||||||
Рассмотрим 3 способа описания движения:
1)векторный
2)координатный
3)естественный
1 |
2 |
3 |
|
|
|
r (t) = r |
x = x(t), y = y(t), z = z(t) |
S = S(t) |
r |
|
dr |
|
r |
|
r |
vx = |
dx |
,vy = |
dy |
|
= |
dz |
vабс = |
dS |
|
< v >= |
S |
||||
v |
= |
|
|
< v |
>= |
|
|
|
,vx |
|
|
|
|
|
|
|||||||
dt |
t |
dt |
dt |
dt |
dt |
|
t |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
= |
= rt′′ |
|
|
′′ |
′′ |
|
′′ |
|
|
|
dv |
|
= St′′ |
|
||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dt |
|
ax = xt |
,ay = yt ,az |
= zt |
a = |
dt |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Кинематика вращательного движения точки.
При вращении материальной точки рассматриваются две величины: ω,ε
r |
Dϕ |
< ω >= |
Dt |
r r
dϕ = ω × dt - элементарное угловое перемещение
Элементарное угловое перемещение характеризуется не только численным значением, но и плоскостью в которой происходит вращение Þ dϕ ^ этой плоскости. Ориентация плоскости определяется перпендикуляром к ней.
Свойством быть вектором обладают лишь элементарные угловые перемещения т. к. если бы конечные перемещения были векторами, то в таких условиях результирующий вектор не равен сумме слагаемыхÞ Dϕ - не вектор.
Угловое перемещение считается вектором, если оно мало и правило сложения векторов выполняется.
r,v,a - естественные векторы
10
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
