то что давала филимонова / Лекции Механика для студентов Физика

О реальности существования сил инерции.

Являются ли силы инерции реальными силами? Они реальны в том же смысле, в каком являются реальными ускорения в неинерциальных системах координат, для описания которых они введены. Они реальны также и в более глубоком смысле: при рассмотрении физических явлений в неинерциальных системах можно указать конкретные физические последст- вия действия сил инерции. Например, в вагоне поезда силы инерции могут привести к увечьям пассажиров, т. е. к весьма реальному и осязаемому результату. Поэтому силы инерции столь же реальны, как реален факт

равномерного и прямолинейного движения тел в инерциальных системах координат, если отсутствуют “обычные” силы взаимодействия, как это формулируется в первом законе Ньютона.

Силы инерции имеют важное практическое применение. Например,

инерциальные системы навигации позволяют определить с большой точностью местоположение самолета или ракеты по приборам, измеряющим силы инерции, без каких-либо измерений положения самолета или ракеты относительно Земли и небесных тел.

Нахождение сил инерции.

Чтобы можно было описать движение тел в неинерциальной системе отсчета с помощью уравнения (1), необходимо указать способ определения сил инерции, фигурирующих в правой части этого уравнения. Силы инерции характеризуют ту часть ускорения тела, которая обусловливается

ускоренным движением системы координат относительно инерциальной системы отсчета. Запишем уравнения движения некоторого тела в неинерциальной и инерциальной системах координат:

где “обычные” силы взаимодействия F одинаковы в обеих системах координат; a′ и a – ускорения соответственно в неинерциальной и инерциальной системах координат.

Из уравнений (2) и (3) для силы инерции получаем

111

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Обычно при рассмотрении неинерциальных систем отсчета используется следующая терминология. Ускорение a относительно инерциальной системы отсчета называется абсолютным, а ускорение a′ относительно неинерциальной системы отсчета – относительным. Формула (4) показывает, что силы инерции обусловливают разность между относительным

иабсолютным ускорениями. Отсюда ясно, что силы инерции существуют только в неинерциальных системах координат. Введение этих сил в уравнения движения, использование их при объяснении физических явлений

иг. д. В неинерциальных системах координат является правильным и

необходимым. Однако использование понятия сил инерции при анализе движений в инерциальных системах координат является ошибочным, поскольку в них эти силы отсутствуют.

Неинерциальные системы отсчета, движущиеся прямолинейно и поступательно.

Выражение сил инерции.

Пусть неинерциальная система движется прямолинейно вдоль оси X инерциальной системы (рис. 3). Ясно, что связь между координатами

некоторой точки дается формулами

переносной и относительной скоростями. Переходя в (6) к ускорениям, находим

112

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

называются соответственно абсолютным, переносным и относительным ус- корениями. Следовательно, в соответствии с определением (4) выражение

для сил инерции в движущейся прямолинейно неинерциальной системе отсчета имеет вид

т. е. сила инерции направлена противоположно переносному ускорению неинерциальной системы.

Маятник на тележке.

Рассмотрим равновесное состояние маятника в неинерциальной системе координат, движущейся в горизонтальном направлении с поступательным ускорением ao (рис. 1). Силы, действующие на маятник, указаны

непосредственно на рисунке. Уравнение движения маятника имеет вид

маятника и вертикалью.

В инерциальной системе координат действующие силы и уравнение движения изменяются (рис. 2). Сила инерции в этом случае отсутствует,

имеются только сила T со стороны натянутой нити и сила тяжести = r .

P mg

Условие равновесия гласит:

Очевидно также, что tgα = ago .

Падающий маятник.

Очень эффектной демонстрацией явлений в прямолинейно движущихся неинерциальных системах является падающий маятник. Маятник подвешен на массивной рамке, которая может свободно падать, скользя с очень малым трением по вертикальным направляющим тросам (рис. 4а). Когда рамка покоится, маятник совершает собственные колебания. Рамка может быть

приведена в состояние свободного падения в любой фазе колебаний маятника. Движение его при свободном падении рамки зависит от того, в какой фазе колебаний началось свободное падение. Если маятник в момент

113

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

второе из которых имеет решение a2 = g , т. е. описывает свободное

падение маятника, а первое полностью совпадает с (13) и описывает вращение вокруг точки подвеса.

В приведенных примерах анализ движения был одинаково прост и на- гляден как в неинерциальной системе координат, так и в инерциальной. Это объясняется тем, что примеры были выбраны именно такими с целью ил- люстрации соотношения между инерциальными и неинерциальными сис- темами. Однако очень часто решение задачи в неинерциальной системе ока- зывается значительно более простым, чем в инерциальной. Например, анализ скатывания цилиндра с наклонной плоскости, которая находится в равно- ускоренном движении в произвольном направлении, значительно проще в неинерциальной системе координат, связанной с наклонной плоскостью, чем в инерциальной системе, в которой плоскость движется ускоренно.

Измерение сил инерции позволяет найти абсолютное ускорение системы координат относительно сферы неподвижных звезд. Соответствующие при- боры называются акселерометрами.

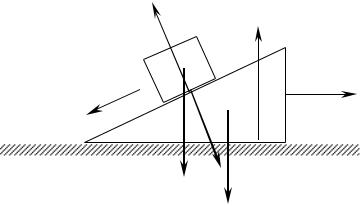
Задача.

Тело массой m1 может скользить без трения по наклонной плоскости бруска массой m2 . Угол наклона плоскости с горизонтом α . Брусок движется

без трения по горизонтальной плоскости (рис. 5). Найти ускорения тела и бруска.

Решение: Обозначим a1 – ускорение тела вдоль наклонной плоскости относительно бруска и a2 – ускорение бруска в горизонтальном направлении. На тело действует сила реакции N1 опоры и вес m1 g . На брусок действует сила реакции N2 опоры и вес m2 g .

Уравнения движения Ньютона для бруска в проекциях на горизонтальное и вертикальное направления записываются в виде:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

а для тела – в виде

Решим теперь эту задачу, если горизонтальная плоскость, на которой находится брусок, движется с ускорением ao вверх.

При решении задачи в инерциальной системе координат в уравнениях (16) и (17) надо учесть изменение сил реакций опор, являющихся след- ствием дополнительного ускорения масс в вертикальном направлении. Однако проще решить задачу в неинерциальной системе отсчета, движу- щейся вертикально вверх с постоянным ускорением. В ней добавляется сила инерции, действующая в вертикальном направлении, и все дело сводится к изменению силы тяжести. Решения для a1 и a2 имеют вид (18), но с

заменой g → g + ao .

Нетрудно решить задачу для произвольного направления ускорения

r . В этом случае в уравнениях (16) и (17) надо учесть действие сил

ao

инерции как в вертикальном, так и в горизонтальном направлении.

Невесомость. Принцип эквивалентности.

Невесомость.

Как было видно на примере падающего маятника, в свободно падающей неинерциальной системе отсчета силы инерции полностью компен- сируют действие силы тяжести и движение происходит так, как если бы не было ни сил инерции, ни сил тяжести. Наступает состояние невесомости. Этим

обстоятельством широко пользуются для создания в земных условиях состояния невесомости, например для тренировки космонавтов.

Состояние невесомости возникает в самолете в процессе его перевода в режим пикирования, если при этом ускорение самолета к земле в каждый момент времени равно ускорению свободного падения. Для продолжи- тельного нахождения в состоянии невесомости обычно весь маневр выпол- няют в режиме “горка”, что позволяет избежать образования больших

углов пикирования и наращивания скорости самолета до слишком больших значений. При этом космонавты испытывают состояние невесомости и имеют

116

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

возможность отработать приемы передвижения по кабине, выполнять различные действия и т. д.

Гравитационная и инертная массы.

Наступление состояния невесомости при свободном падении обусловлено весьма важным физическим фактором, а именно равенством инертной и гравитационной масс тела. Инертная масса характеризует инертные свойства тела, а гравитационная масса – силу, с которой тела притягиваются по закону Ньютона. Гравитационная масса имеет такой же смысл, как, на- пример, электрический заряд при рассмотрении электромагнитных взаимо- действий. Вообще говоря, ниоткуда не следует, что гравитационная и инерт- ная массы тела должны быть пропорциональными, или, что то же самое, равными друг другу (если две физические величины пропорциональны друг другу, то подходящим выбором единиц физических величин можно их сделать /равными друг другу). Докажем, что инертная и гравитационная массы тела пропорциональны друг другу. Сила, действующая со стороны Земли, гравитационная масса которой M г , на некоторое тело, гравитационная

масса которого mг , на поверхности Земли равна

где G – гравитационная постоянная, R – радиус Земли. Если инертная масса тела – m то под действием силы (20) оно приобретает ускорение:

Так как ускорение g для всех тел у поверхности Земли одинаково, то от- ношение их инертных и гравитационных масс одинаково, т. е. инертная и гравитационная массы пропорциональны друг другу. Соответствующим вы-

бором единиц физических величин можно их сделать равными друг другу и говорить о массе вообще, не уточняя, о какой именно массе идет речь.

Именно благодаря тому обстоятельству, что гравитационная и инертная массы равны друг другу, при свободном падении силы инерции

и силы тяжести компенсируют друг друга и исключаются из рассмотрения.

Ввиду того, что равенство инертной и гравитационной масс имеет важное значение, оно было весьма тщательно проверено в различных экспериментах. К настоящему времени можно считать доказанным, что эти массы равны друг другу с точностью, не меньшей 10−12 их значения, т. е.

mг - m £10−12 . mг

Равенство инертной и гравитационной масс имеет и другое следствие:

если система отсчета находится в равноускоренном прямолинейном движении относительно инерциальной системы отсчета (в которой, по определению, отсутствуют поля тяготения), то явления в ней протекают

117

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

так, как если бы имелось поле тяготения, ускорение свободного падения в котором равно ускорению системы отсчета.

Для механических явлений это очевидно. Обобщение этого

Принцип эквивалентности.

Принципом эквивалентности называется ут- верждение о том, что в некоторой системе отсчета

наличие ускорения ее неотличимо от присутствия соответствующего поля тяготения.

Конкретное поле тяготения меняется от одной точки пространства к другой. Поэтому, вообще говоря, нельзя подобрать какую-то систему отсчёта, которая движется таким образом, что её ускорение в каждой точке

пространства эквивалентно по своему действию с имеющимся там полем тяготения. Однако если

необходимо рассмотреть поле тяготения в достаточно малой области пространства, то в первом приближении его можно считать постоянным в этой области. Поэтому в достаточно малой области

пространства всегда можно воспользоваться принципом эквивалентности и сделать определённое заключение о ходе процессов. Проиллюстрируем это на красном смещении.

Красное смещение.

Поле тяготения оказывает важное действие на свет – изменяет его частоту. Неизбежность изменения частоты света в поле тяготения следует из принципа эквивалентности.

Представим себе следующий опыт в поле тяготения Земли. Из некоторой точки испускается луч света частотой ω , распространяющийся в вертикальном направлении (рис. 6). Спрашивается: какой будет частота света на высоте h? На этот вопрос ответить исходя из общих соображений нельзя, поскольку неизвестно действие силы тяжести на частоту. Ответ можно дать с помощью принципа эквивалентности, исходя из того, что в

отсутствие силы тяжести частота при распространении света не изменяется.

Рассмотрим такой опыт в системе координат, которая свободно падает в однородном поле тяжести. В этой системе отсутствуют какие-либо силы, и все процессы внутри нее происходят так же, как в инерциальной системе. Поэтому частота света при распространении не изменяется. Следовательно, наблюдатель, покоящийся в этой системе координат в точке на высоте h, должен воспринимать ту же частоту, которая была излучена в точке О той же системы координат.

118

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Теперь проанализируем тот же опыт из лабораторной системы коор- динат, связанной с Землей, в которой неинерциальная система координат свободно падает. Будем считать, что в момент испускания луча в точке О ско- рость этой системы равна нулю (но ускорение, конечно, не равно нулю, а

равно ускорению свободного падения). За время Dt = hc распространения луча от точки О до точки наблюдения на высоте h свободно падающая система координат приобретает скорость v = gDt = ghc . Следовательно, из-за

эффекта Доплера находящийся в этой системе наблюдатель должен воспринять излучение большей частоты, чем частота испущенного в точке О

света, на Dω = ω vc . Однако анализ явления в неинерциальной системе показал

отсутствие изменения частоты. Отсюда можно заключить, что в процессе распространения света между точкой О и точкой на высоте h произошло

уменьшение частоты испущенного света на Dω = ω cgh2 . Для видимого света это

означает сдвиг соответствующей частоты в сторону красного цвета спектра.

Поэтому эффект уменьшения частоты света при распространении против силы тяжести называется красным смещением.

Значение его в земных условиях очень мало. При разности высот в 10 м для красного смещения получаем следующую оценку:

Заметить такое изменение частоты – примерно то же самое, что заметить недостачу одной секунды в ста миллионах лет. Тем не менее, в 1960 г. удалось это

ничтожное в земных условиях красное смещение надежно зафиксировать. Для этого был использован эффект Мёссбауэра, который заключается в том, что при

определенных условиях фотоны излучаются ядром практически без отдачи. Условие этого излучения без отдачи состоит в том, что импульс отдачи при излучении фотона воспринимается не отдельным атомом, а всей кристаллической решеткой атомов. Эффект Мёссбауэра в том и состоит, что такие условия возможны.

Вследствие излучения без отдачи ширина линии излучения получается очень маленькой, т. е.

испускаемые фотоны имеют разброс частоты в очень малой области. С другой стороны, поглощение фотона также произойдет только тогда, когда его частота почти точно равна частоте испускания без отдачи.

Пусть вещество А (рис. 7) излучает без отдачи фотоны некоторой частоты,

а такое же вещество В при этих же условиях может поглощать фотоны той же частоты. Некоторое число фотонов проходит вещество В, не будучи

119

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

поглощенными, и попадает на чувствительный приемник С, регистрирующий это число.

Допустим, что по каким-то причинам во время распространения фотонов между Л и В их частота изменилась. Тогда они не смогут поглощаться веществом В и их число, попадающее на приемник С, возрастает. Таким образом, обнаруживается малейшее изменение частоты фотона при распространении между Л и В. На той же установке можно измерить, на сколько изменилась частота излучения фотонов. Для этого

необходимо вещество В перемещать по линии распространения луча с такой скоростью и, чтобы благодаря эффекту Доплера частота падающего на него фотона снова стала равной частоте резонансного поглощения. В этот

момент снова заметно возрастет поглощение и упадет интенсивность излучения, воспринимаемого приемником С. Эффект достаточно отчетливо выражен, и скорость v фиксируется с большой точностью. В результате удается измерить изменение частоты фотонов при распространении от Л к В. В опытах 1960 г., повторенных затем неоднократно, высота источника Л над детектором В составляла примерно 15 м. Красное смещение было уверенно зафиксировано и подтвердило формулу (22).

Красное смещение заметно при наблюдении излучения звезд, так как масса у звезд больше, чем у Земли. Например, имеющиеся данные по излу- чению Сириуса подтверждают формулу красного смещения.

Не следует путать красное смещение, которое вызвано полем тяготения, с космологическим красным смещением, обусловленным расширением Вселенной.

Гравитационное красное смещение является прямым следствием замедления течения времени в гравитационных полях.

У поверхности земли течение времени замедлено в сравнении с течением времени на высоте. Следовательно, одному колебанию стандарта

времени на высоте соответствует более чем одно колебание того же стандарта времени у поверхности земли. А это означает, что частота света при приближении к поверхности земли увеличивается, а при удалении – уменьшается.

Неинерциальные вращающиеся системы отсчета.

Кориолисово ускорение.

При рассмотрении неинерциальных систем координат, движущихся по прямой линии, соотношения между абсолютной, переносной и относительной

скоростями и соответствующими ускорениями были совершенно одинаковыми [см. (28.2) и (28.3)]. У вращающихся систем дело обстоит сложнее. Отличие обусловливается тем, что переносная скорость различных точек вращающейся системы координат различна. Абсолютная скорость по- прежнему является суммой переносной и относительной скоростей:

120

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com