то что давала филимонова / Лекции Механика для студентов Физика

Другое важное применение гироскопов —

поддержание заданного направления Движения экипажа, например судна («авторулевой») или самолета («автопилот»). Для этой цели применяются уравновешенные («астатические») гироскопы на кардановом подвесе. В этом случае нет никаких внешних моментов, которые могли бы изменить направление оси гироскопа, и она

сохраняет свое направление в пространстве независимо от движения экипажа. Конечно, осу-

ществить такой вполне свободный гироскоп практически невозможно вследствие неизбежного трения в подшипниках карданова подвеса. Однако

если собственный момент импульса гироскопа велик, а силы трения малы, то моменты этих сил, возникающие при поворотах экипажа, мало

изменяют направление оси гироскопа в пространстве. Поэтому при отклонении направления экипажа от направления, заданного осью гироскопа, рамы карданова подвеса, на котором укреплен гироскоп, поворачиваются от- носительно оси гироскопа так, чтобы ось гироскопа сохранила неизменным свое направление в пространстве. Повороты рам карданова подвеса при помощи тех или иных механизмов превращаются в команды, которые вызывают отклонения рулей, возвращающие экипаж к заданному направлению.

с вертикальной осью, задающей горизонтальную плоскость, в которой должен оставаться самолет, и другой с горизонтальной осью, ориентированной вдоль оси самолета, задающий курс самолета. Оба

гироскопа дают соответствующие команды рулям и другим элементам управления, поддерживающим горизонтальный полет самолета по заданному курсу. Такими автопилотами, освобождающими летчика от необходимости все время управлять самолетом, оборудованы почти все современные самолеты, предназначенные для длительных полетов.

Еще одно важное применение гироскопа в навигации — это гироскопический компас. В гирокомпасах используются свойства не вполне

241

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

свободного гироскопа, ось которого может двигаться только в одной фиксированной плоскости, которую мы для краткости будем называть плоскостью оси, например в плоскости, перпендикулярной к прямой 00' (рис. 11).

Пусть подставка, на которой закреплен такой не вполне свободный гироскоп, вращается с постоянной угловой скоростью со вокруг оси, образующей некоторый угол с плоскостью оси гироскопа. Так как гироскоп не вполне свободен, то со стороны вращающейся подставки на него может действовать некоторый внешний момент. Чтобы определить направление этого момента, разложим угловую скорость вращения подставки ω на составляющие: в плоскости оси ωt и перпендикулярную к ней ωп . Это

второе вращение никак не влияет на гироскоп, так как относительно этой оси он в подставке не закреплен. По отношению к вращению ωt гироскоп не

свободен, и со стороны подставки на гироскоп действует внешний момент M t , направленный по ωt . Под влиянием этого момента ось гироскопа будет

подставку во вращение, то после нескольких качаний ось гироскопа устанавливается в направлении угловой скорости вращения подставки, и притом так, что момент импульса гироскопа по направлению совпадает с направлением угловой скорости (рис. 13). Если изменить направление вращения подставки, то ось гироскопа поворачивается на 180°.

Аналогично будет вести себя не вполне свободный гироскоп под влиянием вращения Земли (рис. 14). Если ось его может вращаться только в горизонтальной плоскости данного места, то под влиянием угловой скорости вращения Земли ω она установится в направлении ωt проекции ω на

горизонтальную плоскость, т. е. в направлении меридиана данного места, причем вектор момента импульса будет иметь направление на север. Таким образом, не вполне свободный гироскоп в комбинации с устройством, удерживающим его в горизонтальной плоскости (например, с гирогоризонтом), может служить компасом.

Гироскопические компасы обладают по сравнению с магнитными рядом преимуществ: на их показания не влияют магнитные бури, находящиеся поблизости массы железа, они менее чувствительны к вибрациям и качке и т. д. Поэтому гирокомпасы сейчас играют важную роль в навигации.

242

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Деформация в твердых телах.

Виды деформаций Закон Гука. Энергия упругих деформаций.

Изменение формы тела под внешним воздействием называется деформацией.

Деформация называется упругой, если она исчезает после снятия нагрузки.

Выделяют два основных вида деформации: растяжение-сжатие и сдвиг. На практике все виды деформации могут быть сведены к этим двум видам деформаций.

Деформация растяжения-сжатия связана с изменением линейных размеров, а деформация сдвига – с параллельным смещением слоев материала относительно друг друга.

Отношение силы к величине поверхности, на которую эта сила действует перпендикулярно, называют нормальным напряжением

σn = Fn / S.

Если сила направлена по касательной к поверхности, то напряжение называют тангенциальным или касательным, а если сила перпендикулярна поверхности, то напряжение называют нормальным.

Закон Гука выражает линейную связь между напряжениями и

относительная деформация растяжения равна единице или, что то же самое,

котором угол сдвига равен 450.

Модуль сдвига в жидкостях и газах равен нулю.

243

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Согласно закону Гука, для деформации кручения угол закручивания зависит от модуля сдвига N и обратно пропорционален радиусу стержня,

нагружения и разгрузки различна, то говорят о механическом гистерезисе.

Энергия упругой деформации линейно зависит от коэффициента

Плотность энергии упругой деформации пропорциональна модулю Юнга и квадрату относительной деформации

Абсолютно упругие тела.

Как уже отмечалось выше, при деформациях возникают внутренние напряжения, силы которых, в общем случае, зависят не только от деформаций, но и от скоростей, с которыми эти деформации происходят. В этом легко убедиться, если взять полимерное вещество, которое при обычных условиях медленно растекается подобно замазке, принимая форму сосуда, в котором оно находится. Можно без особых усилий изменить его форму, если делать это медленно. Однако, если вылепить шарик, то легко обнаружить, что такой шарик обладает хорошими упругими свойствами, подскакивая практически после удара об пол на ту же высоту, с которой он был брошен без начальной скорости. Этот опыт показывает, что силы деформации, подобно силам вязкого трения, возрастают по мере увеличения скорости деформации. В ряде практически важных случаев силы напряжения определяются только деформациями. Такие тела, в которых это имеет место, называются абсолютно упругими телами, или упругими телами.

Замечательным свойством таких тел является способность полностью восстанавливать свою форму после снятия внешних усилий, прикладываемых к телу. Рассмотрим, например, растяжение (или сжатие) стержня (рис. 1.1) с силой F, приложенной перпендикулярно к торцевой грани с площадью сечения S. Опыт показывает, что при последовательном

возрастании нагрузки вначале деформации развиваются равномерно по длине стержня и растут пропорционально нагрузке, т.е.

(1.18)

244

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Величина называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций соответствующим напряжениям выражает закон Гука. Коэффициент пропорциональности называется

коэффициентом удлинения и для каждого материала определяется опытным путем. Так как численные значения гораздо меньше , то - весьма малая величина. Поэтому обычно вводят модуль упругости (модуль Юнга) , и

закон Гука окончательно записывают в виде

(1.19)

Опыт показывает, что этот закон выполняется лишь в определенном интервале напряжений. Если растягивать стержень, последовательно увеличивая от нуля возрастающую силу, то каждый раз, после снятия нагрузки, деформация исчезает. Однако при некотором напряжении появляется заметное остаточное удлинение. Это напряжение называется пределом упругости. На рис. (1.7) изображена зависимость деформаций от напряжений, называемая диаграммой растяжений. Следует отметить, что закон Гука выполняется только в части области упругости - области пропорциональности, когда .

Рис. 1.7.

При возрастании нагрузки наблюдается явление текучести, т.е. внезапный рост удлинения образца при постоянной нагрузке , называемой пределом текучести. Отметим, что течение материала происходит равномерно по всей длине стержня. За пределами области текучести дальнейшее удлинение стержня сопровождаетсяувеличением . Однако деформации будут распределены уже неодинаково по дине стержня (рис. 1.8.) - в некотором месте можно заметить образование шейки. При напряжении , называемом пределом прочности, в этом ослабленном сечении происходит разрыв.

Рис. 1.8.

То напряжение, которое данный материал может выдержать на практике, не

245

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

разрушаясь и не получая опасной деформации, называют допустимым и обозначают . Обычно , и все расчеты проводят на основе законов Гука.

Чтобы обеспечить прочность при всех обстоятельствах допустимое напряжение выбирается как часть предела прочности, в частности, для металлов , а для дерева . Следует отметить, что наибольшие деформации, которые может выдержать материал, не определяются протяженностью области текучести. Если область текучести велика, то материал называется пластичным. Такой материал, как, например, сталь, способен выдерживать большие нагрузки без разрушения. Наоборот, если область текучести невелика, то этот материал хрупок. Хрупкие материалы, как чугун, например, разрушаются при деформациях . Однако в ряде случаев пластичные материалы могут разрушаться и при малых деформациях (например, сталь при температуре ниже С). Аналогичными свойствами обладают и сдвиговые деформации. В частности,

в области пропорциональности связь между деформациями сдвига и касательным напряжением (рис. 1.2) задается соотношением

(1.20)

в котором - касательное напряжение, аналогичное по смыслу введенному выше нормальному напряжению, а G - модуль сдвига, являющийся, как и модуль Юнга, также характеристикой материала.

Из этого можно сделать два важных вывода. Во-первых, поскольку предел пропорциональности на 2-3 порядка меньше модуля упругости, то в области упругости деформации .

Рис. 1.9.

Во-вторых, просматривается связь между величиной модуля Юнга E и модуля сдвига G - чем больше E, тем больше и G. Это не случайно, т.к. между обеими величинами существует жесткая связь. Чтобы ее установить, рассмотрим растяжение маленького кубика с длиной стороны , как это было изображено на рис. 1.9. Обратим внимание, однако, на то, что квадратная грань ABCD параллелепипеда, находящегося внутри рассматриваемого кубика, превращается при деформациях в ромбическую

246

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

грань A'B'C'D'. Совершенно ясно, что параллелепипед испытывает сдвиговую деформацию, а его объем при этом практически не изменился (см. также формулу (1.17)). Величину угла сдвига можно легко связать с деформацией удлинения и коэффициентом Пуассона . Из треугольника A'OD' следует, что

(1.21)

Поскольку , то

(1.22)

Приравнивая правые части (1.21) и (1.22), находим

(1.23)

В последней формуле учтено, что .

Рис. 1.10.

Сила F, растягивающая кубик (рис. 1.10), создает нормальное напряжение . Это напряжение передается на грани AB и BC параллелепипеда, однако силы, действующие на каждую из его граней, имеют не только нормальную к грани, но и направленную вдоль грани параллельную составляющую . Касательное напряжение оказывается при этом равным

(1.24)

Поскольку деформации в формуле (1.23) пропорциональны напряжениям, a , то

(1.25)

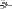
Сравнивая последнее равенство с соотношением (1.20) при учете, что , находим искомую связь между модулями Юнга и сдвига:

(1.26)

В рассмотренном примере следует обратить внимание на то, что величина и направление силы, приложенной к некоторой площадке, зависит от ориентации и величины этой площадки. Так, на грань куба действует сила F, перпендикулярная к грани, в то время как на грань параллелепипеда действует сила F/2, направленная под углом к этой грани. Этот частный

247

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

вывод получит далее обобщение при обсуждении способов задания сил, действующих на каждый из элементов тела. Посмотрим, что будет происходить с тем же кубиком, если его растягивать одновременно силами, приложенными ко всем его граням. В этом случае

относительные удлинения каждой из его сторон будет задаваться соотношениями:

(1.27)

Формулы (1.27) описывают деформации кубика при его всестороннем растяжении или сжатии. Если напряжения одинаковы , то деформации также будут одинаковы: , и

В результате всесторонней деформации новый объем кубика станет равным

а его относительное изменение составит величину

(1.28)

Параметр

(1.28)

называется модулем всестороннего сжатия и играет важную роль в теории упругости. Важно отметить, что хрупкие материалы, подвергнутые всестороннему давлению, на которое дополнительно накладывается растяжение, сжатие или сдвиг, обнаруживают значительные пластические деформации. Такие деформации играют существенную роль, например, в процессах образования рельефа земной коры: граниты и базальты, хрупкие в обычных условиях, текут под действием колоссального давления в глубинных слоях Земли. Деформации растяжения и сдвига возникают в

практически важных случаях изгибов балок строительных конструкций и окруживания валов машин и механизмов.

Коэффициент Пуассона.

При всем многообразии случаев произвольную деформацию тела можно свести к двум элементарным деформациям - растяжению (сжатию) и сдвигу. Обратимся к опыту. Закрепим один конец резинового шнура длиной и потянем за другой конец с постоянной силой. Шнур придет в новое положение равновесия с длиной (рис. 1.1). Такую простейшую

деформацию можно охарактеризовать относительным удлинением

(1.1)

248

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

При этом растяжение соответствует , а сжатию - .

Рис. 1.1.

Деформацию сдвига можно наблюдать в опыте с резиновым кубиком, если закрепить, например, его нижнее основание, а к верхнему основанию приложить касательную силу. (рис. 1.2)Деформация в этом случае будет

характеризоваться параметром

(1.2)

зависящим от угла сдвига , который в большинстве практически важных случаев мал, и .

Рис. 1.2.

Отметим также известный факт, что при растяжении резинового шнура его поперечный размер d уменьшается до величины d1. Такое поперечное сжатие

характеризуется параметром

(1.3)

Опытным путем установлено, что отношение к приблизительно одинаково для разных деформаций одного и того же материала. В теории упругости

материал характеризуется коэффициентом Пуассона

(1.4)

Каково численное значение коэффициента Пуассона? Чтобы ответить на этот вопрос, посчитаем изменение объема резинового шнура. В отсутствие деформации его объем , объем же деформированного шнура

(1.5)

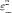
В последнем выражении мы пренебрегли малыми величинами , и . С учетом (1.4) относительное изменение объема запишется в виде

249

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

(1.6)

Поскольку при растяжении () объем никогда не уменьшается, то . Для изотропных материалов, имеющих одинаковые механические свойства по всем направлениям, коэффициент Пуассона , в частности, для металлов .

Понятие о тензоре деформации.

В рассмотренных выше случаях мы имели дело с одномерными однородными деформациями растяжения и сдвига (вдоль одного направления), где и оказывались одними и теми же для всех элементарных объемов резинового шнура. Во многих случаях ситуация гораздо сложнее: с одной стороны, деформации меняются от точки к точке (неоднородные деформации), а с другой стороны не являются одномерными. Последнее означает, что деформации в некоторой точке P описываются тремя деформациями растяжения маленького кубика с т. P внутри (рис. 1.3) и двумя сдвигами каждой из трех граней кубика: . 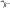Здесь первый индекс i означает, что грань кубика перпендикулярна оси Xi, второй индекс j означает, что грань смещается вдоль оси Xj. Таким образом,

неоднородные деформации в каждой точке тела в общем случае характеризуются набором 9 величин деформаций, являющихся функциями координат. Эти девять величин составляют тензор деформаций, однако независимы лишь 6 его величин.

Рис. 1.3.

Рассмотрим несколько подробнее подход, используемый для описания деформации в некоторой точке P, приводящий к введению понятия тензор деформаций. Пусть тело находится к недеформированном состоянии, и известно положение каждой из его частиц, задаваемых радиус-вектором r относительно некоторой системы координат как, например, положение т. P на рис 1.4. При деформировании все его точки, вообще говоря, смещаются. Смещение каждой точки можно охарактеризовать вектором смещения u(x1, x2, x3), являющегося при неоднородных деформациях функцией координат. Однако деформации в точке будут определены лишь тогда, если известно смещение соседних с т. P частиц тела. Таким образом, задание смещения

250

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com