Временные характеристики интегрирующих звеньев
Идеальное дифференцирующее звено имеет уравнение
и передаточную функцию
,
где – коэффициент пропорциональности. Амплитудно-фазовая частотная характеристика
,
имеет
действительную часть
и мнимую
,
а на графике (рис. 3.10 б) совпадает с мнимой
осью. Логарифмическая амплитудная
частотная характеристика имеет вид
прямой с единичным положительным
наклоном (то есть при увеличении частоты
ω на одну декаду величина
также увеличивается на одну декаду) и
проходит через точку
,
.
Логарифмическая
фазовая частотная характеристика идет
горизонтально во всем диапазоне частот
на высоте
(см. рис. 3.10 в). Переходная функция
идеального дифференцирующего звена
имеет вид дельта-функции (см. рис. 3.10 г)
с площадью импульса, равной
:
.
Рис. 3.10. Идеальное дифференцирующее звено:
а) передаточная функция;
б) амплитудно-фазовая характеристика; в) логарифмические амплитудная и фазовая характеристики; г) переходная функция
Рис. 3.11. Примеры дифференцирующих звеньев:
а) тахогенератор постоянного тока;
б) ОУ в режиме дифференцирования;
Временные характеристики дифференцирующих звеньев
Лекция 4 Частотные характеристики сау Частотные характеристики динамического звена
Наряду с математическим описанием (дифференциальные уравнения, передаточные функции, временные характеристики) динамических звеньев и систем автоматического управления в целом в теории автоматического управления для математического описания звеньев и систем широко применяются также частотные характеристики, которые определяют поведение отдельных звеньев и системы в целом при действии на их входе гармонических колебаний.
Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме (т. е. вынужденные синусоидальные колебания звена).
Известно,
что гармонические колебания
,
(A – амплитуда; φ – фаза; ω – частота
колебаний) описываются периодической
функцией времени
,
где
– период колебаний; n – любое целое
число.
Отличительной особенностью периодических
функций является то, что они существуют
на бесконечном отрезке времени от
до
.
С этой точки зрения они являются
математической абстракцией, т. к. любой
реальный процесс имеет начало и конец.
Однако, если реальный процесс длится
достаточно долго с периодическим
повторением предыдущих значений, то
его можно с достаточной точностью
считать периодическим.
Таким образом, в реальных условиях реакцией системы на периодические входные воздействия могут считаться только установившиеся колебания выходной величины, т. е. колебания, которые возникают в САУ по истечении достаточно большого времени после начала воздействия.
В этом принципиальное отличие метода частотных характеристик от метода временных характеристик, так как в последнем рассматривается поведение САУ в переходных режимах.
Несмотря на это, как увидим дальше, частотные характеристики также полно определяют поведение во времени управляемой величины, вызванное как периодическими, так и непериодическими воздействиями.
В линейной САУ установившиеся колебания выходной величины, вызванные гармоническими воздействиями на входе, являются гармоническими колебаниями той же частоты, но амплитуда и фаза их будут уже другими.
На вход линейного звена в момент времени подан сигнал, изменяющийся во времени по синусоидальному закону:
где
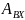– амплитуда входного сигнала; часто
принимают
–
круговая частота колебания
;
– период колебаний;
–
начальная фаза, обычно принимают
.
Спустя некоторое время, достаточное
для затухания свободной составляющей
движения, на выходе звена установятся
вынужденные колебания. При этом выходная
переменная будет изменяться тоже по
синусоидальному закону с той же частотой
,
но с другой амплитудой
и сдвинута по фазе относительно входной
синусоиды на угол
:
,
Если теперь повторить эксперимент для другого значения частоты , то на выходе будут наблюдаться вынужденные колебания с другой амплитудой и другим фазовым сдвигом .
Изменяя частоту входного сигнала в
диапазоне
0, можно получить амплитудную частотную
характеристику (АЧХ) – зависимость
отношения амплитуд выходного и входного
сигналов
от частоты – и фазовую частотную
характеристику (ФЧХ)
– величину фазового сдвига выходной
синусоиды относительно входной.
В ряде случаев бывает удобно амплитудную и фазовую частотные характеристики заменить одной – амплитудно-фазовой частотной характеристикой, – которая на комплексной плоскости может быть представлена в показательной форме:
.
По сути
и
– это параметрические уравнения
переменного от частоты
годографа
вектора
в полярной системе координат.
Если уравнение вектора
представить в параметрической форме
в декартовых координатах, то
,
где P
– вещественная частотная характеристика;
Q
–
мнимая частотная характеристика.
В электрических цепях вещественной
частотной характеристике P
соответствует активная составляющая
выходной переменной (тока или напряжения),
а мнимой Q
– реактивная. Очевидна связь между
частотными характеристиками, заданными
в полярной и декартовой системах
координат:
и
.
Запишем гармонические функции входа и выхода динамического звена в символической (комплексной) форме:
;
.
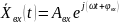И взяв их отношение, получим:
При изменении частоты от 0 до +∞ получаем
комплексную функцию частоты W(jω), которая
называется амплитудно-фазовой частотной
характеристикой динамического звена.
Ее модуль
определяет отношение амплитуд выходных
и входных колебаний при изменении
частоты ω от 0 до +∞. Эта зависимость
отношения амплитуд выходных и входных
гармонических сигналов от частоты
называется амплитудно-частотной
характеристикой (АЧХ) динамического
звена (рис. 4.1).
Рис. 4.1. Амплитудно-частотная характеристика динамического звена
Аргумент
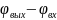выражения
(4.1) определяет разность фаз выходных и
входных колебаний. Зависимость разности
фаз выходных и входных гармонических
сигналов от частоты называется
фазочастотной характеристикой (ФЧХ)
динамического звена (рис. 4.2).
Рис. 4.2. ФЧХ динамического звена