Лекция 7

Я сюда сначала напишу критерий Найквиста, потому что мы его не успели разобрать на прошлой лекции, а затем статические и астатические системы.

Критерий устойчивости Найквиста

Критерий Найквиста позволяет судить об устойчивости замкнутой САУ (рис. 7.10) по амплитудно-фазовой частотной характеристике разомкнутой системы.

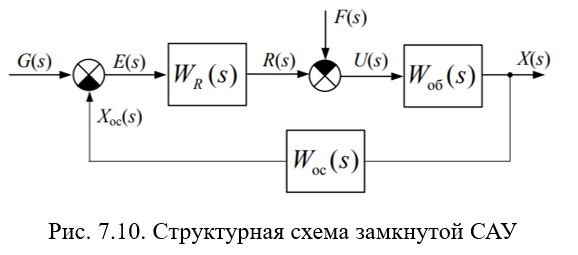
Передаточная функция замкнутой системы относительно сигнала рассогласования по задающему воздействию (видимо W_ос=1?):

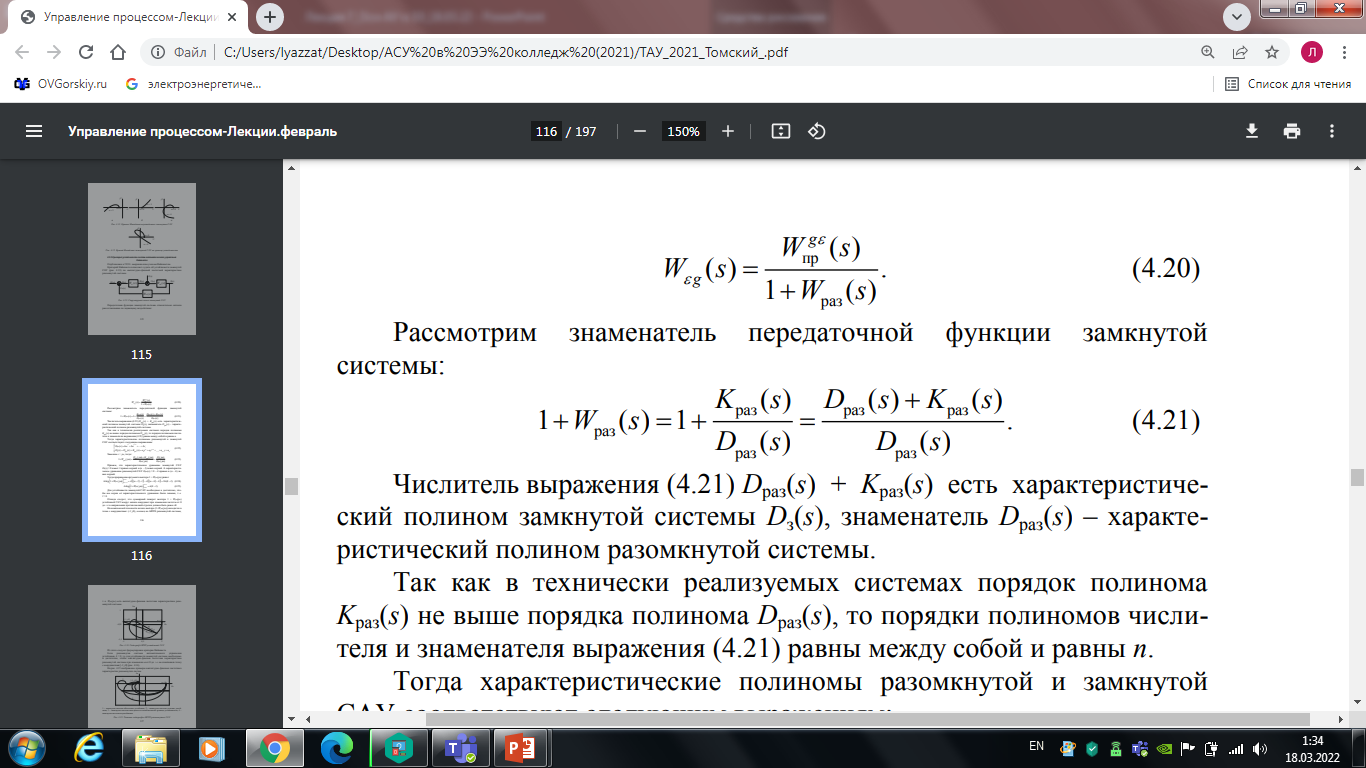(7.20)

Рассмотрим знаменатель передаточной функции замкнутой системы:

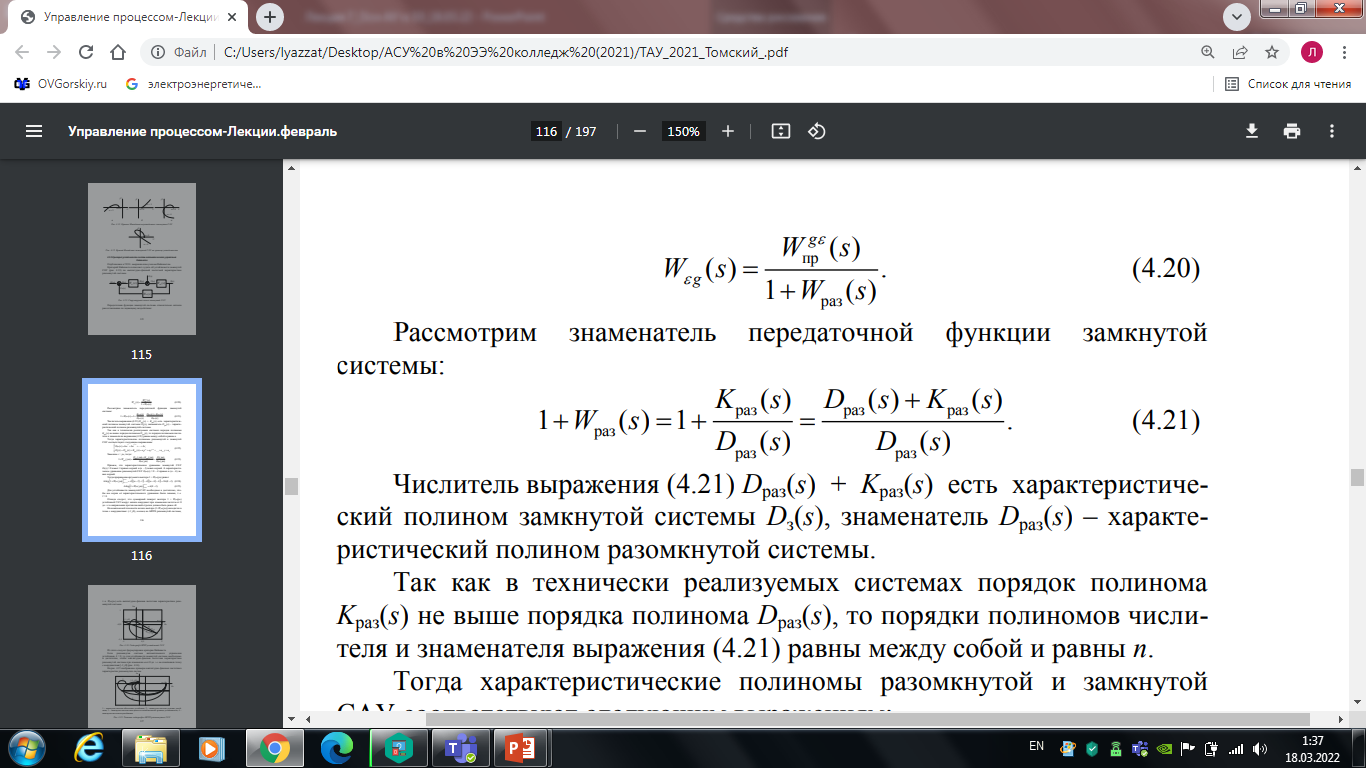(7.21)

Числитель выражения (7.21) D_раз(s)+K_раз(s) есть характеристический полином замкнутой системы D_з(s), знаменатель D_раз(s) – характеристический полином разомкнутой системы. Так как в технически реализуемых системах порядок полинома K_раз(s) не выше порядка полинома D_раз(s), то порядки полиномов числителя и знаменателя выражения (7.21) равны между собой и равны n.

Тогда характеристические полиномы разомкнутой и замкнутой САУ соответствуют следующим выражениям:

(7.22)

(7.23)

Примем, что характеристическое уравнение замкнутой САУ D_з(s)=0 имеет l правых корней и (n–l) левых корней (тут имеется в виду вещественная часть положительная и отрицательная). А характеристическое уравнение разомкнутой САУ D_раз(s) = k правых и (n–k) левых корней.

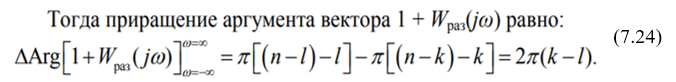
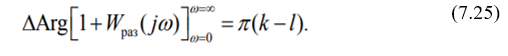
Бля, я честно не знаю, как эти аргументы были посчитаны, тут надо подумать толково, а мне лень, поэтому ниже попытался объяснить. Но она тоже не знает, откуда они берутся, так что пофиг.

Если как-то по-простому объяснять, то у нас есть числитель и знаменатель. Когда умножаем комплексные числа, то углы складываются, когда делим, то вычитаются. У нас числитель (D_з(s)=0) имеет l правых корней и (n–l) левых корней. Нам важны левые корни, потому что они нам дают отрицательную вещественную часть и поворот против часовой стрелки, который как раз берётся со знаком плюс. Теперь, когда мы меняли ω от 0 до +∞, то мы умножали количество корней на угол π/2, а здесь мы меняем ω от -∞ до +∞, поэтому умножаем и на угол π.

Для устойчивости замкнутой САУ необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми, т. е. l = 0.

Отсюда следует, что суммарный поворот вектора 1+W_раз(jω) устойчивой САУ вокруг начала координат при изменении частоты от 0 до 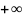в направлении против часовой стрелки должен быть равен .

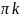На комплексной плоскости начало вектора (1+W_раз(jω)) находится в точке с координатами: (-1; j0), а конец на АФЧХ разомкнутой системы, т.к. W_раз(jω) есть амплитудно-фазовая частотная характеристика разомкнутой системы.

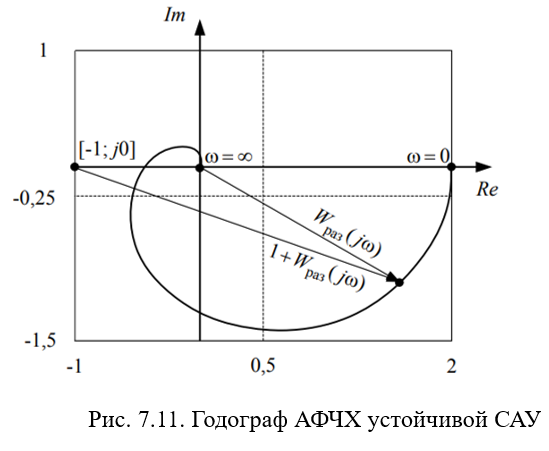
Из этого следуют формулировки критерия Найквиста.

1) Если разомкнутая система автоматического управления устойчивая (k=0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении от 0 до +∞ не охватывала точку с координатами [-1; j0] (рис. 7.11).

2) Если же разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ неустойчивой разомкнутой системы (k>0) при изменении частоты от 0 до +∞ охватывала точку 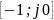в положительном направлении k/2 раз, где k – число правых корней характеристического уравнения разомкнутой системы.

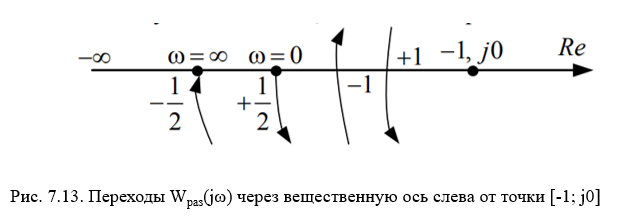
Назовём переход W_раз(jω) через вещественную ось слева от точки , т.е. через интервал 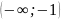, положительным, если он идет сверху вниз, и отрицательным, если он идет снизу вверх. Если W_раз(jω) начинается на интервале при 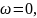или заканчивается на нем при 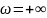, то в этих случаях считают, что она совершила полперехода.

На рис. 7.12 изображены примеры амплитудно-фазовых частотных характеристик разомкнутых систем.

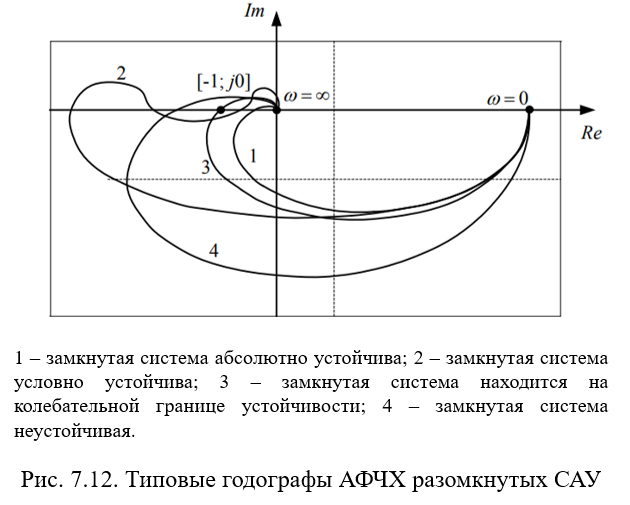
Тогда критерий Найквиста можно сформулировать так: 3) если разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФЧХ разомкнутой САУ через отрезок вещественной оси 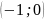при изменении частоты от 0 до +∞ была равна k/2, где k – число правых корней характеристического уравнения разомкнутой САУ.

Опять пример с кучей формул, просто картинкой вставлю.

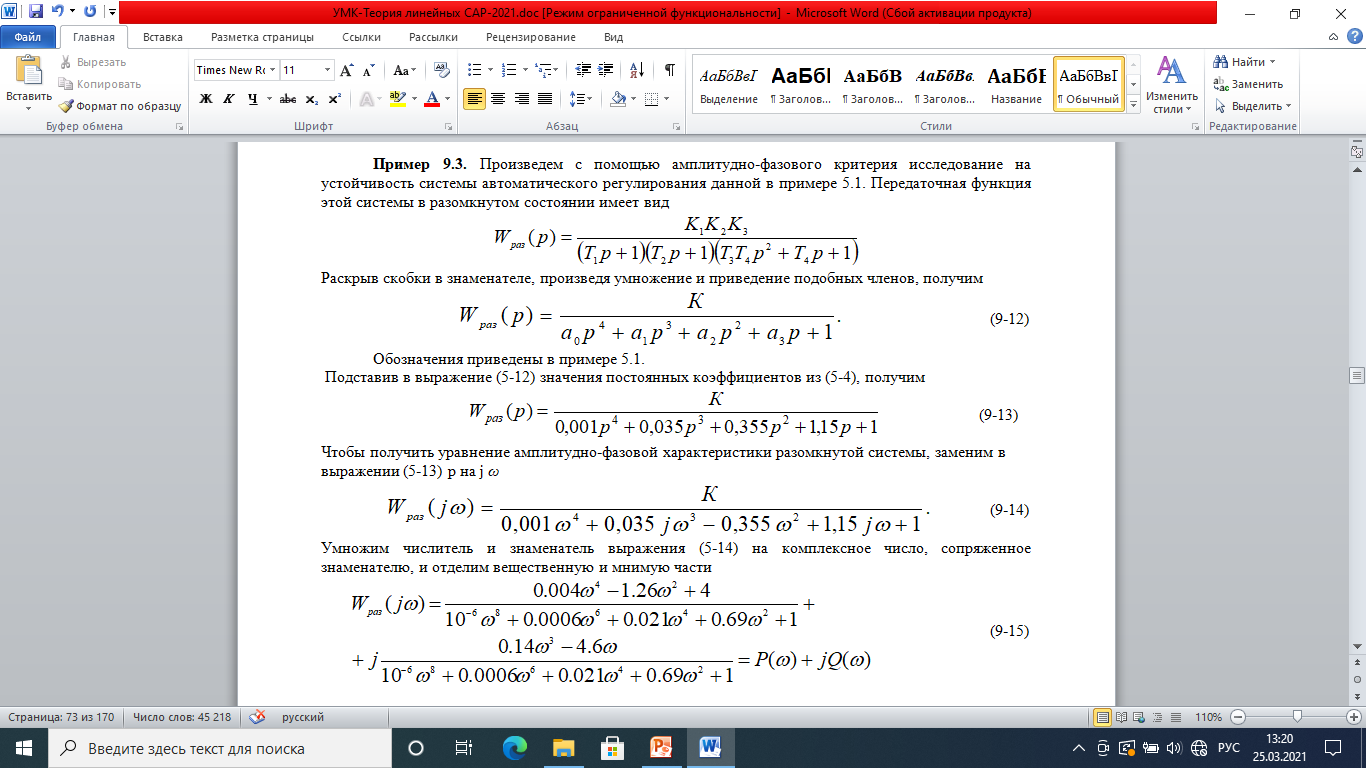
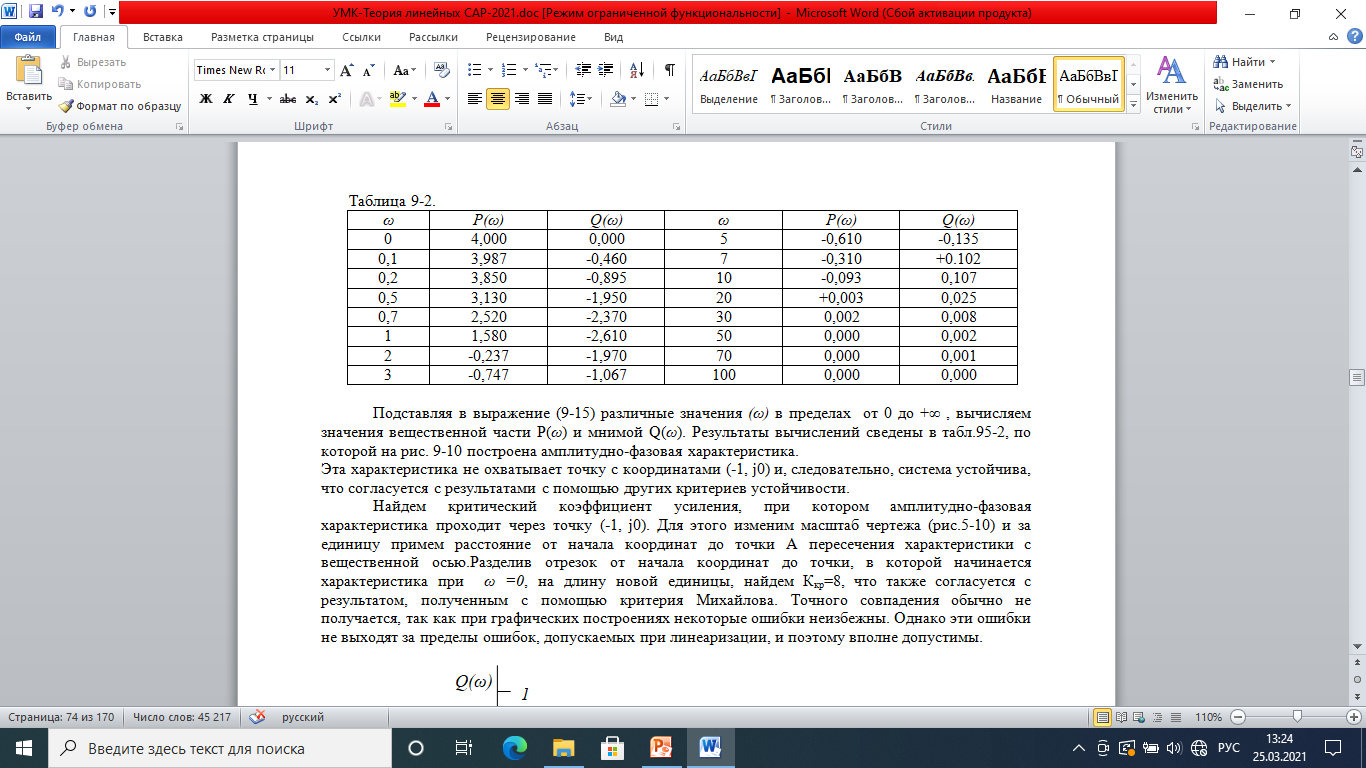
Подставляя в выражение (9-15) различные значения ω в пределах от 0 до +∞ , вычисляем значения вещественной части Р(ω) и мнимой Q(ω). Результаты вычислений сведены в табл.9-2, по которой на рис. 9-10 построена амплитудно-фазовая характеристика.

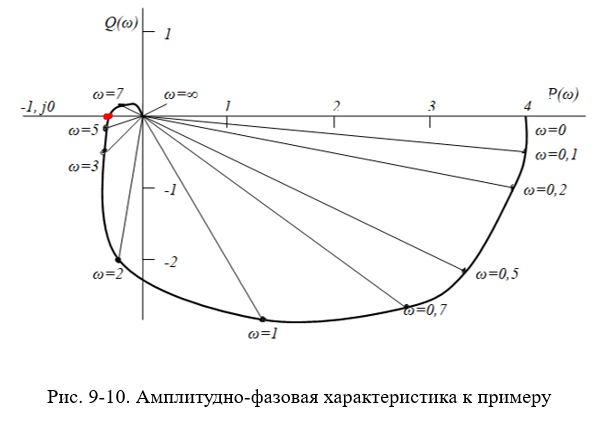
Эта характеристика не охватывает точку с координатами (-1, j0) и, следовательно, система устойчива, что согласуется с результатами с помощью других критериев устойчивости.

Найдём критический коэффициент усиления, при котором амплитудно-фазовая характеристика проходит через точку (-1, j0). Для этого изменим масштаб чертежа (рис.9-10) и за единицу примем расстояние от начала координат до точки А (красная точка) пересечения характеристики с вещественной осью. Разделив отрезок от начала координат до точки, в которой начинается характеристика при ω =0, на длину новой единицы, найдём К_кр=8, что также согласуется с результатом, полученным с помощью критерия Михайлова. Точного совпадения обычно не получается, так как при графических построениях некоторые ошибки неизбежны. Однако эти ошибки не выходят за пределы ошибок, допускаемых при линеаризации, и поэтому вполне допустимы.