Линеаризация уравнения, описывающего динамическое звено
Линеаризацию удобнее производить по
звеньям. Допустим, что в звене A
выходная величина y
является нелинейной функцией одной
входной величины x
(рис. 2.1 а). При
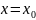имеем
.
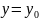Пусть входная величина x
получила относительно начального
значения
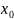приращение
,
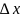так что
.
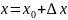Тогда приращение выходной величины
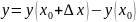
Дифференциал функции y, определяемый как главная часть ее приращения, при данном значении независимой переменной x равен значению производной при этом значении, умноженному на дифференциал независимой переменной:
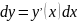
Тогда для малых
.
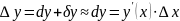Здесь
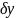– малая величина более высокого порядка,
чем
,
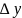и которая обычно отбрасывается. В случае
необходимости величину погрешности
можно оценить, разложив функцию
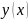в ряд Тэйлора в окрестности точки
.
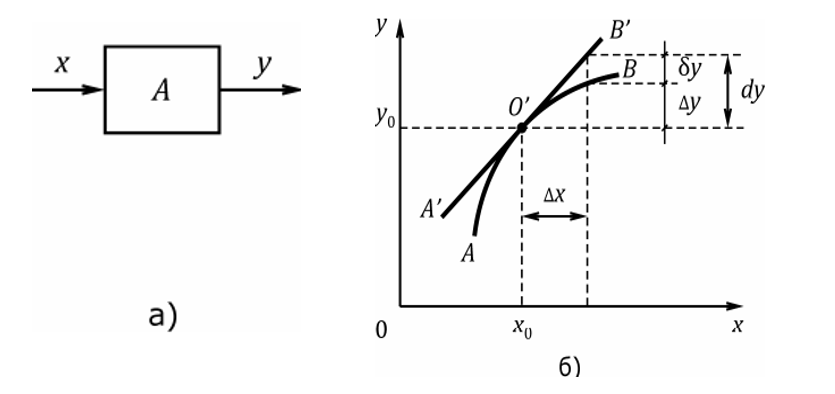Рис.
2.1. Нелинейное звено (а) и его статические
характеристики (б):
АВ – исходная,
А′В′ - линеаризованная
Замена точного значения приращения
функции её дифференциалом в окрестности
принято называть линеаризацией
зависимости
.
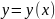Геометрически линеаризация нелинейной
зависимости между переменными x
и y (см. рис. 2.1 б) означает
замену исходной кривой AB
отрезком её касательной
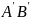в точке
,
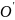соответствующей заданному режиму, и
параллельному переносу начала координат
в эту точку.
Пример 2.1.
Нелинейное статическое звено описывается
уравнением
.
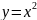Выполните линеаризацию характеристики
этого звена вблизи точки
.
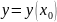Имеем:
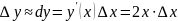
При получим
.
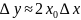Видим, что коэффициент усиления
линеаризованного звена зависит от
величины входного сигнала x.
В частности, при
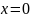он равен нулю.
Стандартная форма записи дифференциальных уравнений. Передаточные функции систем регулирования
Процессы в линейных системах автоматического регулирования и их элементах обычно описываются дифференциальными уравнениями. При этом члены, содержащие выходную величину y и её производные, записываются в левой части уравнения, а воздействия x и f и их производные – в правой:
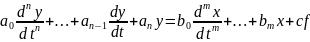(2.1)
Здесь
,
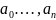и
–
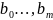коэффициенты (параметры) уравнения. В
большом числе случаев их можно принять
постоянными. В тех случаях, когда они
изменяются во времени, а скорость этого
изменения соизмерима со скоростью
процессов управления в системе, то эту
систему принято называть нестационарной,
или системой с переменными параметрами.
Уравнение (2.1) системы регулирования удобно представить в символической (операторной) форме, заменив символ дифференцирования оператором p:
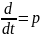
тогда
.
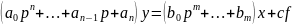(2.2)
Разделив все члены полученного уравнения
на коэффициент
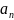при выходной переменной y,
получим стандартную форму дифференциального
уравнения системы регулирования:
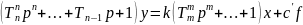(2.3)
Здесь
;
.
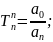
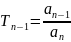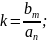
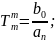
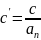Многочлен, стоящий в скобках при выходной
переменной y,
принято называть собственным
(характеристическим) оператором, а при
входной величине x
– входным оператором, или оператором
воздействия. Коэффициенты
,
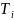имеющие размерность времени, называют
постоянными времени.
Операция замены
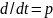носит название алгебраизации
дифференциального уравнения (2.1). В
линейных системах с постоянными
параметрами звеньев она формально
соответствует преобразованию Лапласа,
в котором функции
,
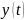заданной во времени t и
называемой оригиналом, ставится в
соответствие функция
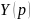комплексной переменной p,
определенная интегралом
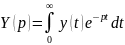
и называемая изображением функции по Лапласу.