Синусоидальная (гармоническая) функция времени

Эту функцию задают в виде синусоидального сигнала частоты ω и амплитуды A_ВХ (см. рис. 2.2 в).

При анализе конкретных систем регулирования рассматривают лишь вынужденную составляющую движения, когда выходная переменная изменяется также по синусоидальному закону с той же частотой ω, но с другой амплитудой A_ВЫХ и сдвинута по фазе относительно входной синусоиды на угол φ.

Линейная функция времени. Эта функция (см. рис. 2.2 г) описывается уравнением

,

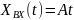где A – постоянная величина.

Когда линейная функция используется для изучения процессов в системе регулирования, то рассматривается только вынужденная составляющая движения. Этот вид воздействия чаще всего используется в следящих электроприводах, например, станков с числовым программным управлением.

Динамическое звено сау

Для математического описания работы САУ удобно разбивать ее не на функциональные элементы автоматики, а на динамические звенья. Поэтому вводится понятие динамического звена. Динамическим звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида. Приведенное определение является общим. Под него подходит любой элемент автоматики, совокупность таких элементов и даже вся система автоматического управления в целом.

3 Передаточные функции сау 3.1 Передаточная функция динамического звена

Понятие передаточной функции динамического звена связано с операционным методом решения дифференциальных уравнений, основанном на применении преобразования Лапласа-Карсона. Преобразованием Лапласа называют соотношение:

(3.1)

где x(t) – оригинал; X(p) – изображение, ставящее функции x(t) вещественного переменного t в соответствие функцию X(p) комплексной переменной p (p = σ + jω).

Преобразование Карсона имеет вид:

. (3.2)

Обратное преобразование Лапласа:

(3.3)

Теорема смещения:

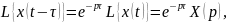
(3.4)

Связь конечного значения функции с изображением:

(3.5)

Изображение производных функций:

Рассмотрим пример. Пусть динамическое звено (рис 3.1) описывается дифференциальным уравнением:

= (3.7)

 

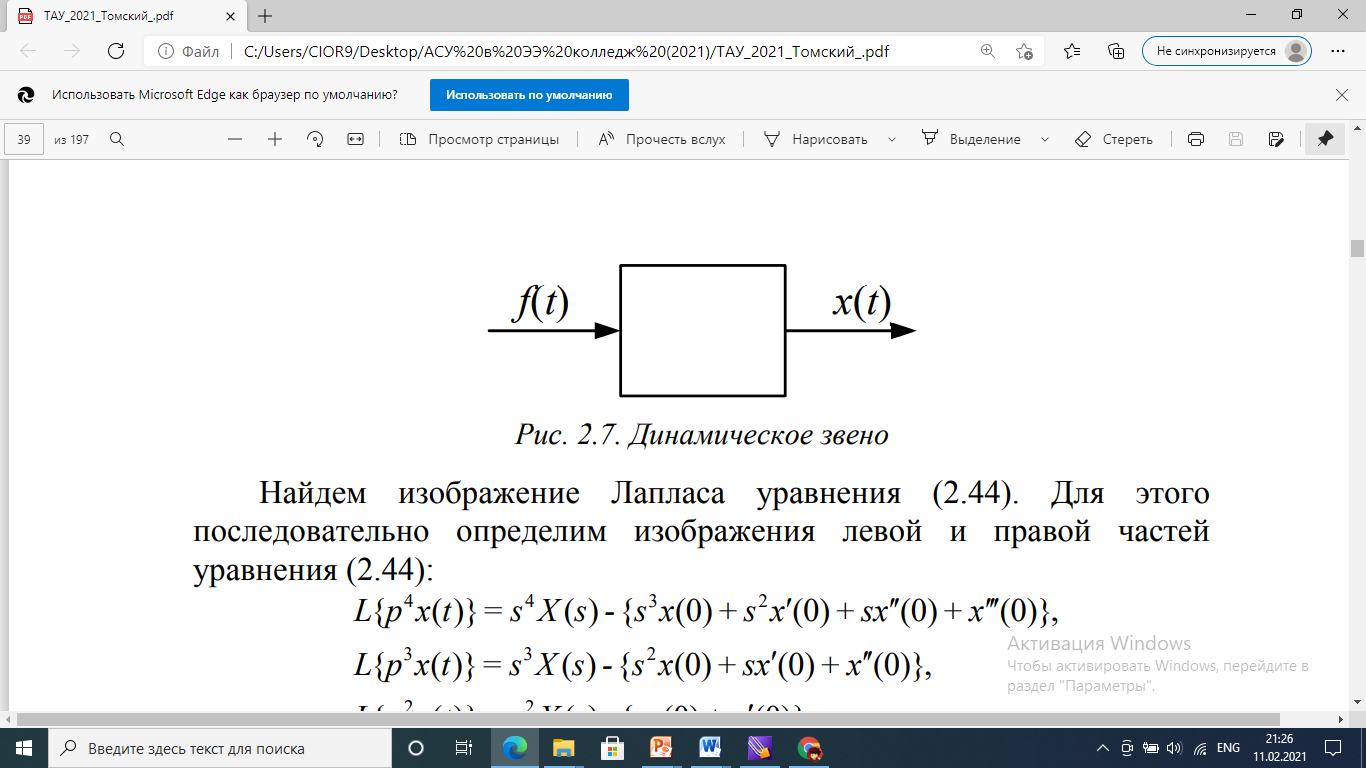
Рис. 3.1. Динамическое звено

Найдем изображение Лапласа уравнения (3.7). Для этого последовательно определим изображения левой и правой частей уравнения (3.7):

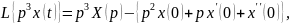
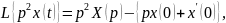
(3.8)

С учетом (3.8) изображение уравнения (3.7) при нулевых начальных условиях принимает вид:

(3.9)

Тогда отношение изображения выходной координаты к изображению входной координаты рассматриваемого звена при нулевых начальных условиях примет вид:

. (3.10)

В общем виде передаточная функция динамического звена запишется:

. (3.11)

Таким образом, передаточная функция динамического звена есть отношение изображения (Лапласа-Карсона) выходной координаты звена к соответствующему изображению входной координаты звена при нулевых начальных условиях.

При этом изображение выходной координаты динамического звена (рис. 3.2) равно где – передаточная функция динамического звена, а – изображение входного воздействия.

Рис. 3.2. Динамическое звено