Выделение областей устойчивости

С помощью рассмотренных выше критериев устойчивости можно определить, устойчива ли система автоматического регулирования с заданными параметрами. Однако критерии не дают возможности определить, в каких пределах можно менять тот или иной параметр или два параметра одновременно, чтобы система оставалась устой­чивой. Это можно сказать с помощью некоторых критериев устойчи­вости лишь по отношению к коэффициенту усиления.

Впервые вопросом выделения областей устойчивости занялся И. А. Вышнеградский. Он решил эту задачу применительно к си­стемам, описываемым дифференциальными уравнениями третьего порядка.

В 1947 г. Ю. И. Неймарк разработал метод выделения областей устойчивости линеаризованных систем по одному комплексному или по двум вещественным параметрам для систем, описываемых дифференциальными уравнениями любого порядка. Этот метод по­лучил название Д-разбиения.

Идея Д-разбиения заключается в следующем. Пусть задано характеристическое уравнение системы автоматического регулирования, в котором все коэффициенты, кроме двух известны и неизменны.

Построение областей устойчивости в плоскости параметров системы автоматического управления. D–разбиение.

При исследовании устойчивости большое практическое значение имеет построение областей устойчивости в плоскости одного или каких-либо двух параметров, влияние которых на устойчивость исследуют, а также построение семейства областей устойчивости в плоскости двух параметров при различных фиксированных значениях третьего параметра. Уравнение границ областей устойчивости можно находить, пользуясь любым критерием устойчивости. Часто для этих целей используют критерий Михайлова.

Понятие о d–разбиении

Характеристическое уравнение замкнутой системы n–порядка имеет вид:

(9.1)

или

(9.2)

где .

Представим себе n–мерное пространство, по координатным осям которого отложены коэффициенты уравнения (9.2). Это пространство называют пространством коэффициентов. Каждой точке пространства коэффициентов соответствуют конкретные численные значения коэффициентов уравнения (9.2) и соответствующий им полином n-го порядка. Уравнение (9.2) имеет n корней, расположение которых на комплексной плоскости корней зависит от численных значений коэффициентов .

Если изменять коэффициенты уравнения (9.2), то его корни, в силу их непрерывной зависимости от коэффициентов, будут перемещаться в комплексной плоскости корней, описывая корневые годографы.

Чтобы представить расположение корней геометрически, рассмотрим характеристическое уравнение третьего порядка (n = 3).

. (9.3)

Если взять три взаимно-перпендикулярные оси и откладывать по ним значения коэффициентов , , , то получим трехмерное пространство коэффициентов, каждой точке которого (рис. 9.1) соответствует вполне определенный полином (9.3) и вполне определенные три корня в комплексной плоскости корней (рис. 9.2).

Рис. 9.1. 3-мерное пространство коэффициентов полинома .

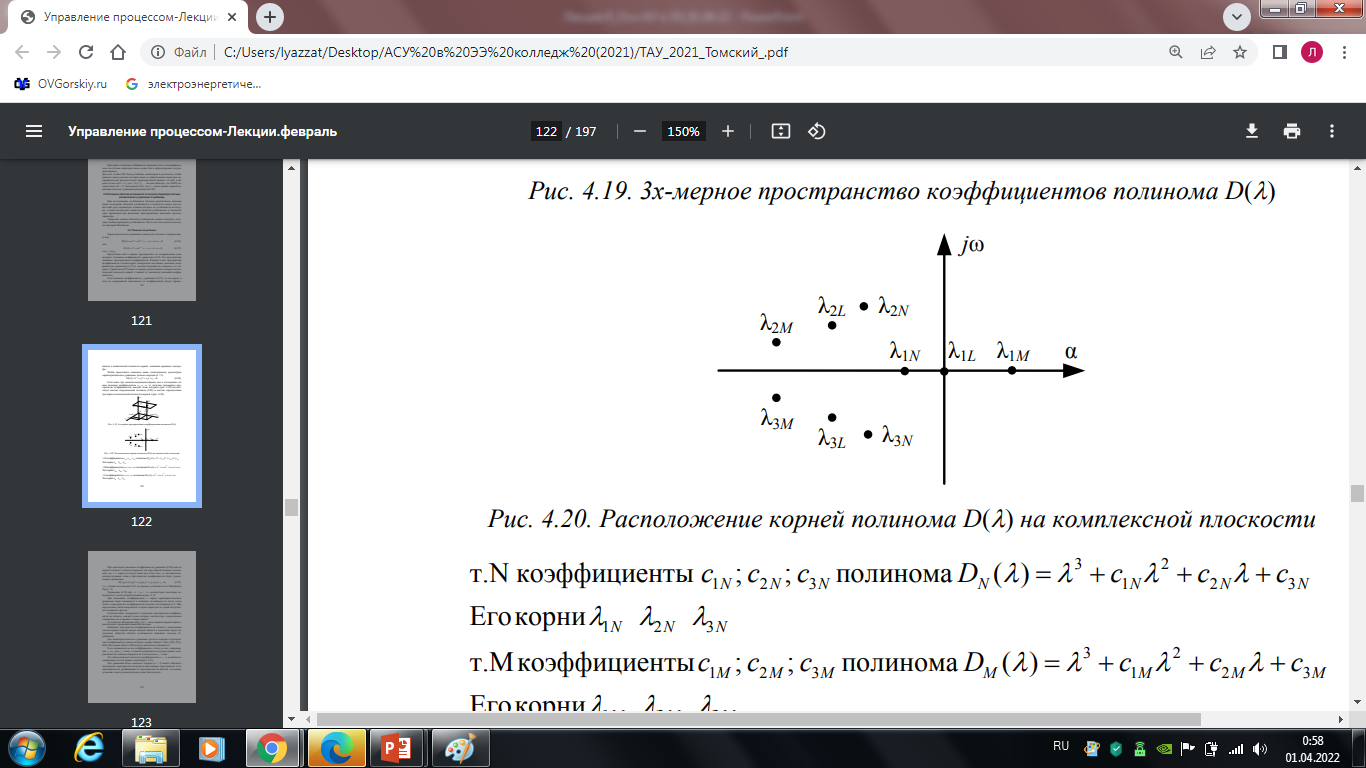
Рис. 9.2. Расположение корней полинома на комплексной плоскости

При создании реальной системы управления бывает необходимо знать не только запас устойчивости, который можно оценить с помощью какого-либо критерия, но и всю область устойчивости по параметрам. Этой цели служит метод D-разбиения, позволяющий построить такую область в плоскости одного или двух параметров.

Рассмотрим суть метода D-разбиения по одному параметру D, который входит в характеристическое уравнение системы линейно:

(9.3)

Заменив в уравнении (9.1) р на , получим уравнение

(9.4)

соответствующее границе устойчивости согласно критерию Михайлова.

Разрешим его относительно D:

. (9.5)

Получили комплексное представление параметра D, что позволяет изобразить его в виде вектора на комплексной плоскости. Конкретное числовое значение частоты определяет положение вектора . При изменении со в диапазоне от до его конец выписывает на комплексной плоскости кривую D-разбиением, представляющую собой границу устойчивости (её также можно рассматривать как отображение мнимой оси плоскости корней).

Кривая D-разбиения симметрична относительно вещественной оси (рис. 9.3) поэтому достаточно построить её часть, соответствующую положительным значениям частоты, а вторую половину получить отображением относительно вещественной оси.

Рис. 9.3. Иллюстрация построения кривой D-разбиения:

1—3 — подобласти с различным распределением корней

Отметим, что эта кривая разбивает комплексную плоскость на несколько подобластей с различным соотношением корней. Для определения области устойчивости необходимо выбрать по одному значению D в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном значении D, то она будет устойчива и при всех его значениях из этой области.

Обычно в качестве параметра D фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т.д.), который может иметь только вещественные значения. Представление его комплексным выражением носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.

Метод D-разбиения можно применять и для построения области устойчивости по двум параметрам  и , которые входят линейно в характеристическое уравнение

(9.6)

В этом случае уравнение границы устойчивости имеет вид

(9.7)

и распадается на два независимых уравнения:

(9.8)

Эти два уравнения параметрически задают кривую D-разбиения. Область устойчивости определяется аналогично случаю одного параметра D.

Пример 9.1. Определить область устойчивости системы (рис. 9.2) по коэффициенту усиления

Рис. 9.4. Структурная схема системы к примеру 9.1

Решение

Определим передаточную функцию замкнутой системы:

.

Запишем её характеристическое уравнение:

.

Здесь k — параметр, по которому строится область устойчивости, поэтому обозначим его через D. Разрешим характеристическое уравнение относительно D и заменим p на . В результате получим уравнение для кривой D-разбиения

.

Вычислим значения вещественной и мнимой части при конкретных положительных значениях частоты и занесем их в таблицу.

Для построения всей кривой D-разбиения полученную половину отобразим относительно оси абсцисс (рис. 9.5).

Как видим, кривая D-разбиения разделила плоскость параметра на две подобласти (1 и 2). Выбираем по одному вещественному значению D в каждой из них и оцениваем устойчивость. Исследуемая система имеет второй порядок, поэтому необходимым и достаточным условием устойчивости её является положительность всех коэффициентов характеристического уравнения. Следовательно, первая область есть область устойчивости .

Рис. 9.5. Кривая D-разбиения для исследуемой системы

Допустим, что при некоторых значениях и часть корней числом m лежит в правой комплексной полуплоскости, а другая часть числом n-m лежит в левой комплексной полуплоскости. На рис. 9.6 общее число корней n=7, m=2, n-m=5.

Известно, что между коэффициентами алгебраического уравнения и распределением его корней на комплексной плоскости существует непрерывная зависимость. При изменении значений коэффициентов уравнения положение корней на плоскости меняется. Последовательным изменением коэффициентов можно добиться того, что один из вещественных корней или два сопряжённых комплексных корня попадут на мнимую ось, а затем перейдут в другую полуплоскость и, таким образом, произойдёт изменение распределения корней между полуплоскостями. Изменяя значения коэффициентов и, можно добиться, чтобы все корни переместились в левую комплексную полуплоскость, и система стала устойчивой.

Однако изменения коэффициентов всегда можно произвести в таких пределах, что корни, перемещаясь, будут оставаться в той же полуплоскости и, таким образом, распределение корней останется прежним. На плоскости коэффициентов и можно выделить область значений этих коэффициентов, при которых все корни будут находиться в левой комплексной полуплоскости, и система будет оставаться устойчивой. Это и будет область устойчивости. При значениях коэффициентов, выходящих за пределы этой области, система теряет устойчивость. Границей области устойчивости являются значения коэффициентов, при которых хотя бы один корень находится на мнимой оси.

Таким образом, границей устойчивости является отображение мнимой оси комплексной плоскости на плоскости коэффициентов. На рис. 9.7. в плоскости коэффициентов выделена область, в которой m=0, (т.е. корни в правой полуплоскости отсутствуют), являющаяся областью устойчивости.

Уяснив идею Д-разбиения, перейдём к рассмотрению правил выделения областей устойчивости по одному параметру (комплексному или вещественному, который является частным случаем комплексного) и по двум вещественным параметрам.

Д-разбиение плоскости одного параметра. Пусть какой-нибудь параметр Б (например, постоянная времени) входит линейно (в первой степени) в несколько коэффициентов характеристического уравнения, которое в этом случае можно записать в виде:

Рис. 9.6. Распределение корней на комплексной плоскости

Считаем параметр Б переменным. Обычно он выражается рядом вещественных чисел. Можно считать эти числа комплексными, имеющими свою плоскость, на которую отображается мнимая ось плоскости корней. Из выражения (9-22) получим:

Чтобы получить значения параметра Б, при которых хотя бы один корень находился на мнимой оси, в выражении (5-23) оператор р заменяем мнимым числом j и отделяем в полученном комплексном числе вещественную и мнимую части

Чтобы получить все возможные значения параметра Б, соответствующие всем возможным мнимым корням, задаём в выражении (9-24) значения в пределах от -∞ до +∞, вычисляем соответствующие значения Р( ) и 0( ) и строим в этих координатах линию, которая является отображением мнимой оси плоскости корней на комплексную плоскость параметра Б или, иначе, границей Д-разбиения по параметру Б (рис. 9-8)

Рис. 9.7. Пример Д-разбиения плоскости параметров

Рис. 9.8. Д-разбиение одного параметра

В устойчивой системе все корни находятся слева от мнимой оси, если двигаться в направлении от -∞ к +∞. Поскольку линия Д-разбиения является отображением мнимой оси, то область устойчивости также будет находиться слева от этой линии, если двигаться по ней в направлении от значения ω = -∞ к значению ω = +∞. Чтобы выявить область устойчивости, на линию Д-разбиения наносится штриховка слева при указанном перемещении -∞ к +∞.

Область, внутрь которой направлено больше штриховки, возможно является областью устойчивости. На рис. 9.8 –это область I. С помощью любого критерия устойчивости проверяется устойчивость системы для любой точки вещественной оси, лежащей в интересующей нас области. Если система устойчива для этой точки, значит, данная область является областью устойчивости. Может случиться, что область устойчивости отсутствует. Следовательно, система неустойчива при любом значении рассматриваемого параметра.

Мы построили кривую, которая разбивает нашу область на несколько подобластей. На рисунке 9.8. изображены три области и необходимо понять, в какой из них система устойчива, а в какой нет. Можно воспользоваться критериями устойчивости, которые были рассчитаны выше, а можно воспользоваться штриховкой. Где есть штриховка, там система устойчива и критерии можно не считать.

Это соответствует действительности, так как с помощью других критериев ранее определили, что при значении К=4 система устойчива. Из рассмотрения кривой Д-разбиения видно, что система остаётся устойчивой при -1<K<8,1