Жесткая обратная связь охватывает инерционное звено

Предположим, что инерционное звено с передаточной функцией

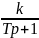
дифференциальным уравнением

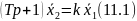
охвачено обратной связью с коэффициентом связи β (рис. 11.4).

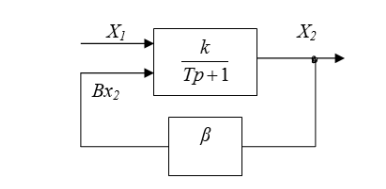
Рис. 11.4. Инерционное звено, охваченное жесткой обратной связью

Передаточная функция инерционного охвачена, охваченного отрицательной связью

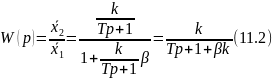
Из выражения (11.2) находим уравнение инерционного звена, охваченного отрицательной обратной связью

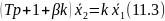
Вынесем за скобки в левой части (1 + 𝛽)

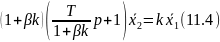
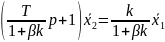
При положительной обратной связи (β>0)

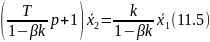
Обозначив

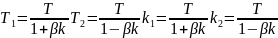
Получим

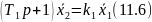
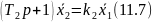
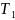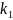Структура этих уравнений не отличается от структуры уравнения инерционного звена без обратной связи (11.1). При отрицательной обратной связи [уравнения (11.4) и (11.6)] качественных изменений инерционного звена не происходит, имеет место уменьшение постоянной времени звена и его коэффициента усиления <𝑇; <𝑘.

При положительной обратной связи и 𝛽𝑘 <1 качественное изменение инерционного звена не происходит, а увеличиваются постоянная времени звена и его коэффициент усиления 𝑇₂> 𝑇; 𝑘₂> 𝑘.

Если при положительной обратной связи 𝛽𝑘>1, то инерционное звено становится неустойчивым и ухудшает динамические свойства системы.

Отрицательная жесткая обратная связь увеличивает быстродействие системы и может снизить ее устойчивость и даже сделать неустойчивой.

В рассмотренных примерах предполагалось, что жесткая обратная связь безынерционна. Однако иногда жесткая обратная связь может иметь постоянную времени ТС, например, если для жесткой связи используется обмотки возбуждения электрических машин, обладающие значительной индуктивностью. В этом случае цепь обратной связи представляет инерционное звено с передаточной функцией

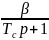
Произведя преобразования, аналогичные приведенным выше, получим уравнения звена, охваченного жесткой отрицательной обратной связью,

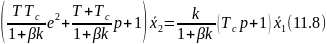
или звена, охваченного жесткой положительной обратной связью,

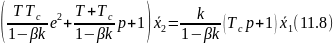
Для уравнений (11.8) и (11.9) оказываются справедливыми все рассуждения, относящиеся к уравнениям (11.6) и (11.7). Дополнительной особенностью является то, что с увеличением 𝑇𝑐 влияние отрицательной обратной связи при прочих равных условиях уменьшается, так как 𝑇𝑐 входит в числитель и компенсирует влияние слагаемого 𝛽𝑘, входящего в знаменатель членов уравнений (11.8) и (11.9).

Влияние жесткой обратной связи на охватываемое ею колебательное звено аналогично влиянию на инерционное звено: отрицательная жесткая обратная связь уменьшает постоянное времени и коэффициент усиления, положительная – увеличивает их. Поэтому охват колебательного звена отрицательной жесткой обратной связью для улучшения динамических свойств может применяться только в структурно-устойчивых системах.

Гибкие обратные связи и их влияние на динамические свойства системы

Гибкие обратные связи отличаются тем, что они действуют в переходных режимах и не действует в установившихся. При введении гибкой обратной связи на вход охваченного ею звена подается величина, пропорциональная скорость изменения выходной величины этого звена, т.е. производная от выходной величины этого звена.

Электрические гибкие обратные связи осуществляется с помощью дифференцирующих трансформаторов и цепей, содержащих емкости. Механические гибкие обратные связи выполняются обычно в виде масляного катаракта (демпфера) с пружиной.

Рассмотрим влияние гибкой обратной связи на динамические свойства системы автоматического регулирования. Предположим, что имеется одноконтурная система автоматического регулирования, передаточная функция которой в разомкнутом состоянии

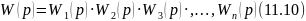
где 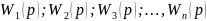- передаточные функции отдельных последовательно соединенных звеньев.

Введем гибкую обратную связь с передаточной функцией 𝑊_с(𝑝) , охватывающую одно из звеньев, например второе. Передаточная функция этого звена с учетом обратной связи.

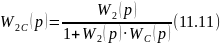
Подставив значение W_2C(p) в выражение (11.10) вместо 𝑊₂(𝑝), получим передаточную функцию разомкнутой системы с местной обратной связью

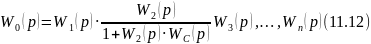
или

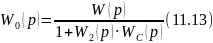
Если обратная связь охватывает несколько последовательно соединенных звеньев, то в знаменатель уравнения (11.13) вместо 𝑊2 𝑝 следует подставить произведение передаточных функций звеньев, охваченных обратной связью.

Уравнение амплитудно-фазовой характеристики системы с обратной связью

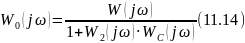
Уравнение амплитудно-фазовой характеристики системы без обратной связи можно представить в показательной форме

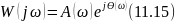
где 𝐴(𝜔) и 𝜃(𝜔) - соответственно амплитудная и фазовая частотные характеристики разомкнутой системы без местной обратной связи.

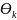
Уравнение амплитудно-фазовой характеристики знаменателя уравнения (11.14) также можно представить в показательной форме

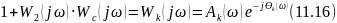
Подставив в выражение (11.14) значения числителя и знаменателя, из выражений (11.15) и (11.16) получим

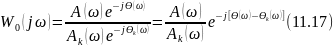
Из выражения (11.17) видно, что при введении гибкой обратной связи модуль вектора амплитудно-фазовой характеристики при любой частоте ω равен частному от деления модуля вектора амплитудно-фазовой характеристики системы без обратной связи на модуль вектора 𝑊𝑘(𝑗𝜔), а аргумент равен разности фаз этих векторов.

Таким образом, введение гибкой обратной связи уменьшает модуль амплитудно-фазовой характеристики системы без обратной связи, что уменьшает динамическую точность и быстродействие системы и поворачивает его в положительном направлении (против часовой стрелки) на угол 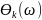что приводит к повышению устойчивости системы.

С увеличением частоты ω действие гибкой обратной связи уменьшается, так как выражение (11.16), входящее в знаменатель формулы (11.17), стремится в этом случае к единице. В установившемся режиме действие гибкой обратной связи полностью прекращается.

Достоинства параллельных корректирующих устройств:

1. Стабильность характеристики системы повышается за счет звеньев, охваченных обратной связью, и поэтому требования к стабильности параметров этих звеньев могут быть менее жесткими, чем требования к неохваченной обратной связи звеньями. Это становится очевидным на основании следующих рассуждений.

Уравнение амплитудно-фазовой характеристики разомкнутой системы, часть звеньев которой охвачена отрицательной обратной связью, имеет вид

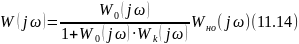
где 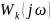, , 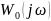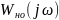- соответственно уравнения амплитудно-фазовой характеристик корректирующего устройства и звеньев, охваченных и не охваченных обратной связью.

В диапазоне существующих частот при достаточно мощном корректирующем устройстве

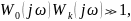
поэтому в выражение (11.18) единицей в знаменателе можно пренебречь. После сокращения получим

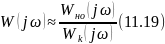
Из выражения (11.19) следует, что амплитудно-фазовой характеристика скорректированной системы не зависит от параметров звеньев, охваченных обратной связью.

2. Системы с параллельными корректирующими устройствами малочувствительны к помехам, накладывающимися на основной сигнал, пропорциональный отклонению регулируемой величины. Это объясняется тем, что вход обратной связи включен на выход охваченных обратной связью звеньев, которые выполняют функцию фильтра низких частот, снижающего уровень помех.

3. Применение параллельных корректирующих устройств не требует применения дополнительных усилителей, так как уровень мощности на выходе звеньев, охватываемых обратной связью, бывает достаточно высоким.

Недостатки параллельных корректирующих устройств:

• Относительная дороговизна и громоздкость (например, стабилизирующих трансформаторов и др.).

• Затруднения в некоторых случаях при суммировании основного сигнала и сигнала, поступающего по обратной связи (иногда технически неосуществимо).