Корневые методы оценки качества управления

Для косвенной оценки качества управления используют корневые показатели, определяемые по расположению корней характеристического уравнения замкнутой системы на комплексной плоскости. (дальше s=p, как и раньше бывало)

При известной передаточной функции замкнутой САУ переходная характеристика системы может быть вычислена при помощи обратного преобразования Лапласа (Карсона) по формулам разложения Хевисайда:

(8.6)

где корни характеристического уравнения системы, - первая производная характеристического полинома по s при .

Из формулы (8.6) видно, что на характер переходного процесса влияют и числитель и знаменатель передаточной функции замкнутой системы. Если числитель не имеет нулей (т. е. представляет собой постоянную величину), то характер переходных процессов можно оценивать по её полюсам, т. е. корням характеристического уравнения замкнутой системы .

Устойчивость и качество переходного процесса определяется графиком переходной составляющей, которая представляет собой решение однородного уравнения

где λ_i - корни характеристического уравнения замкнутой системы

(8.7)

Тогда переходная характеристика и её показатели качества полностью определяются распределением полюсов W_g(s), т. е. корнями характеристического уравнения (рис. 8.6).

Рис. 8.6. Распределение корней характеристического уравнения, ближайших к мнимой оси: а – комплексно-сопряжённых; б – вещественных

При оценке качества переходных процессов САУ рассматривают устойчивую систему: все коэффициенты уравнения (8.7) положительные и его корни λ₁; λ₂; …; λ_n располагаются слева от мнимой оси комплексной плоскости. Некоторой обобщённой оценкой числового значения коэффициентов уравнения (8.7) и его корней может служить параметр

(8.8) (там умножение, а не запятые!)

называемый среднегеометрическим корнем.

Параметр Ω косвенно характеризует быстродействие системы. Увеличение Ω в С раз ведёт к тому, что форма переходной функции не изменяется, а время регулирования уменьшается в С раз. Для увеличения Ω следует увеличивать передаточный коэффициент разомкнутой системы .

Если все отношения последующего коэффициента к предыдущему заключены между положительными числами m и M, т. е.:

то модули всех корней заключены между теми же числами m и M:

Точнее область расположения корней характеристического уравнения принято определять параметрами (рис. 8.6).

Параметр , называемый степенью устойчивости, есть расстояние от мнимой оси до ближайшего корня, т. е. минимальная величина его вещественной части 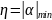. Приближенная связь между параметрами и прямыми показателями качества переходной характеристики заключается в следующем.

Корни характеристического уравнения, расположенные ближе к мнимой оси, т.е. имеющие наименьшую по абсолютной величине вещественную часть, дают составляющие переходной функции, которые затухают наиболее медленно.

Если ближайший к мнимой оси корень – вещественный (рис. 8.6, б), то наибольший вклад в величину времени регулирования вносит наиболее инерционная составляющая переходного процесса: , тогда (рис. 8.7):

Рис. 8.7. График, иллюстрирующий зависимость времени регулирования от наиболее инерционной составляющей

Если же ближайшими к мнимой оси являются два сопряжённых комплексных корня (рис. 8.6, а), то доминирующей будет одна колебательная составляющая, которая затухает также по экспоненциальной составляющей .

Поэтому по степени устойчивости можно приближённо определить время регулирования:

(8.9)

Колебательные свойства системы управления предопределяет та k-ая пара комплексных корней 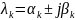, для которой наибольшее отношение или наибольший угол φ между двумя симметричными лучами (рис. 8.6).

Отношение мнимой части к действительной части доминирующей пары комплексных корней называют степенью колебательности.

(8.10)

Значение степени колебательности позволяет определить приближенное значение перерегулирования переходной характеристики:

(8.11)

Колебательность связана с еще одним показателем качества переходной характеристики - со степенью затухания:

(8.12)

Взаимозависимость и определяется следующими формулами:

; (8.13)

В САУ допускают ≥ (90 ÷ 98) %. При = 98% допустимая колебательность ≈ 1,57, при = 90% - μ = 2,72. В практических расчётах используют также корневой показатель колебательности

также определяемый через доминирующую пару комплексных корней. При выборе настроек регуляторов стремятся получить значения m = 0,2 ÷ 0,5.

Опять пример картинкой.

Рис. 11.3. Кривая переходного процесса, построенная по решению упрощённого дифференциального уравнения

Рис.11.4. Ограничение области расположения корней

Показатели, определяемые методом распределения корней, не всегда учитывают влияние возмущений и это является принципиальном недостатком метода.

Метод распределения корней характеристического уравнения даёт далеко не полное представление о качестве переходного процесса. Более полную картину можно получить при рассмотрении влияния на показатели качества распределения полюсов и нулей передаточной функции системы. Подробно этот вопрос изложен в первоисточниках, а здесь приведём только окончательные результаты без доказательств.

Качество переходного процесса обычно рассматривают при нулевых начальных условиях и при воздействии на входе типа единичного скачка

Нулями передаточной функции называется корни многочлена, стоящего его числителе.

Полюсами передаточной функции называются корни многочлена стоящего в её знаменателе (корни характеристического уравнения системы).

Изображение воздействия также может иметь нули и полюсы. В рассматриваемом конкретном примере изображение воздействия не имеет нулей и имеет один полюс расположенный в начале координат комплексной плоскости.

Очевидно, если менять значения нулей и полюсов передаточной функции в выражении (11-20), что достигается изменением параметров системы, то будет меняться изображение регулируемой величины и соответственно будут меняться показатели качества переходного процесса.

При детальном исследовании этого вопроса выявили следующие зависимости.

1. Если нули передаточной функции совпадают с полюсами изображения воздействия или находятся в близи от них, то воздействия вызывают не большие отклонения регулируемой величины. Если нули передаточной функции удаляются от полюсов изображение воздействия, то влияние воздействий на переходный процесс увеличивается.

2. Если один или несколько полюсов передаточной функции системы и изображения воздействия совпадают, то наступает явление резонанса и кривая переходного процесса очень существенно отличается от кривой воздействия. Чтобы кривая переходного процесса по возможности точнее воспроизводила кривую задающего воздействия, необходимо полюсы передаточной функции удалять от полюсов изображения воздействия.

3. Чем дальше полюсы передаточной функции расположены от мнимой оси, тем меньше собственные колебания системы и быстрее затухает переходный процесс.

4. Если нули передаточной функции располагаются в близи полюса, ближайшего к мнимой оси, колебательность переходного процесса уменьшается, при удалении нулей от этого полюса колебания возрастают.

Таким образом, изменением параметров системы можно существенно улучшить показатели качества переходного процесса.