4.4. Кинетическая теория идеального газа

Основное уравнение кинетической теории идеального газа. С точки зрения молекулярно-кинетической теории, газ считается идеальным, если можно пренебречь потенциальной энергией взаимодействия его молекул (по сравнению с кинетической энергией) и размерами молекул (по сравнению со средним расстоянием между ними). Давление газа на стенку возникает в результате многочисленных упругих соударений молекул между собой и со стенками сосуда. (Удар можно считать в среднем упругим, так как газ находится со стенкой в тепловом равновесии). Вследствие беспорядочного движения молекул и равновероятности всех направлений можно считать, что всех молекул N в объеме V движется вдоль оси х, – вдоль оси у, – вдоль оси z. Основное уравнение кинетической теории идеального газа выражает давление через средний квадрат скорости молекул v²:

р = nv = nm₀v² = n_пост = n ,

г

де n = – концентрация молекул, m₀ – масса одной молекулы,  = m₀v – ее импульс, v² = – квадрат средней квадратичной скорости молекул, _пост =   - средняя кинетическая энергия поступательного движения молекул. Если связь энергии и импульса отличается от классического, то равенство, например, для газа фотонов, имеющих импульс  = , в результате приобретает вид р = n.

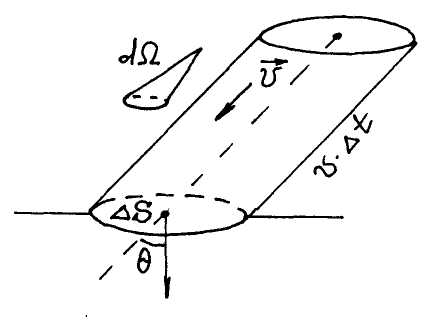
Число молекул ∆N, величину энергии ∆Е и т. д., которые переносятся через площадку ∆S за время ∆t, получают разбиением молекул на группы по скоростям в интервале значений от v до v + dv и по направлению в телесном угле dΩ (рис. 4.9).

П

Рис. 4.9

Рис. 4.9

ри этом число молекул данной группы в единице выделенного объема (например, косого цилиндра, направляющая которого равна (v∆t) и составляет угол  с осью х) равно:

dn(v, v + dv, dΩ) = dn (v, v + dv) .

Все молекулы в выделенном цилиндре попадут на площадку ∆S за время ∆t. Произведя последовательное интегрирование, можно получить соотношения для числа частиц и для величины энергии, которые переносятся через ∆S за время ∆t, соответственно:

и .

В кинетической теории газов доказывается, что если две подсистемы могут обмениваться энергией, то в состоянии равновесия оказываются равными средние кинетические энергии поступательного движения их молекул. Исходя из этого, кинетическая теория газов определяет температуру как величину, пропорциональную средней кинетической энергии поступательного движения молекулы:

_пост = kT,

где k – постоянная Больцмана, которая выражается через универсальную газовую постоянную и число Авогадро. Коэффициент пропорциональности выбран так, чтобы уравнение состояния идеального газа

р = nkT = kT

совпадало с уравнением pV = RT.

Средняя квадратичная скорость поступательного движения молекул вычисляется по формулам:

v_квадр = ,

где  = m₀n – плотность газа.

Степени свободы молекул. Важной характеристикой идеального газа является число степеней свободы его молекул i. У одноатомной молекулы есть только три степени свободы, соответствующие поступательному движению: i = i = 3. У жесткой двухатомной молекулы, кроме поступательных, есть еще две вращательные степени свободы (полярные углы, задающие ее направление в пространстве): i = i + i = 3 + 2 = 5. У жесткой многоатомной (нелинейной) молекулы – три вращательные степени свободы, поэтому i = 6. В классической статической физике доказывается теорема о равнораспределении энергии по степеням свободы: на любую степень свободы, которой в выражении для энергии молекулы соответствует член х² или  , приходится средняя энергия kT в расчете на одну молекулу. Средняя энергия одной молекулы и внутренняя энергия всего газа принимают вид:

 = i_фkT, U = N  = i_фRT.

Физическое число степеней свободы i_ф в случае жестких молекул совпадает с математическим i. Однако, когда оказываются возбужденными колебательные степени свободы (при Т ~ 10³ К), то на каждую колебательную степень свободы будет приходиться (с учетом потенциальной энергии колебаний) средняя энергия kT. В результате получим

i_ф = i_пост + i_вращ + 2i_кол,

где i_кол обозначает математическое число колебательных степеней свободы. Для N – атомной молекулы i_кол = 3N – ( i_пост + i_вращ ).

С учетом степеней свободы получим выражения для теплоемкостей идеального газа и его показателя адиабаты:

C = , C = ,  = .

Закон Дальтона гласит, что давление смеси (двух) идеальных газов равно сумме их парциальных давлений (давление, которое имел бы газ смеси, если бы он один занимал объем смеси):

р = р₁ + р₂ = (n₁ + n₂)kT = (₁ + ₂)RT.

Внутренняя энергия смеси равна сумме внутренних энергий:

U =  RT +  RT.

Эта формула позволяет вывести следующие соотношения:

- эффективное число степеней свободы: i (₁ + ₂) = i₁₁ + i₂₂,

- эффективные молярные теплоемкости:(₁+ ₂)C = ₁C + ₂C ,

- эффективную молярную массу: (₁ + ₂) = ₁₁ + ₂₂.

Распределение Максвелла. Распределение молекул по скоростям описывается следующими функциями:

(v )dv = , (v)dv = ,

(v)dv dv dv = .

Определение любой функции распределения основано на утверждении, что доля молекул, попадающих (в среднем) в очень маленький интервал данной переменной (скорости, проекции скорости, энергии), пропорциональна ширине этого интервала (dv обозначает физически, а не математически, бесконечно малый интервал – он должен содержать большое число молекул). Средняя доля молекул, обладающих некоторым признаком (например, попадающих в заданный интервал скоростей), можно трактовать как вероятность того, что произвольная молекула обладает признаком. Поэтому функцию распределения иногда называют плотностью вероятности.

Перечислим свойства функции распределения (на примере (v)):

Доля частиц (вероятность) в конечном интервале (v₁, v₂):

.

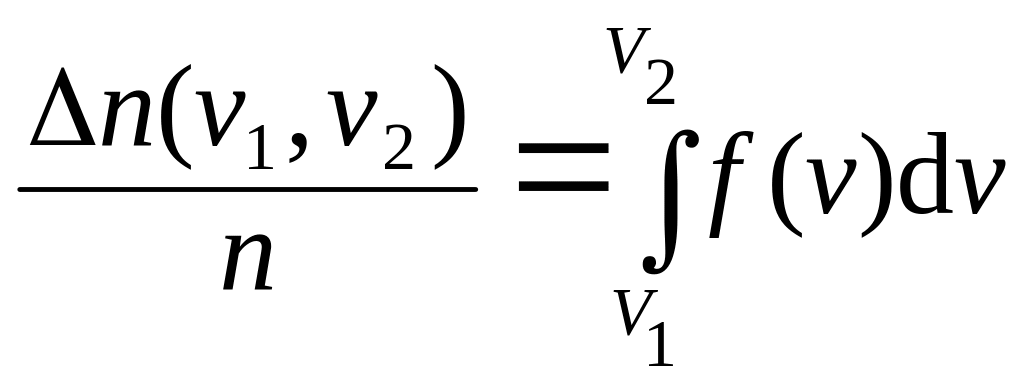Нормированность:

.

Вычисление среднего от любой функции скорости (v):

(v) = .

Между тремя функциями распределения существует следующие связи:

(v) = (v)4v²,

Функция  является четной функцией, то есть можно написать:  = (v ).

Функция ( ) зависит только от v² = v_x² + v_y² + v_z². Связь между  и  удовлетворяется только функцией . Коэффициенты А и  определяются из двух условий а) нормировки функции , б) требования, чтобы  v_x² = , v² = . Ответ выглядит так:

=

(v) = 4v².

Обычно именно последнюю формулу называют распределением Максвелла (рис. 4.10).

Ф

Рис. 4.10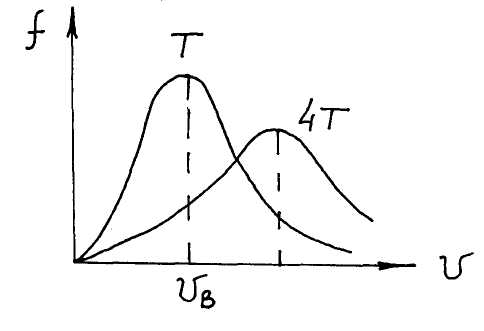

ункция (v) достигает максимума при скорости v_E = , которую называют наиболее вероятной скоростью. Значение функции (v) в этой точке равно

(v_E) = 4e .

Например, при увеличении Т в 4 раза максимальная скорость станет в 2 раза больше, а соответствующее значение функции (v_E) – в 2 раза меньше, но площадь под кривой, в данном случае равная единице, не изменится.

Средняя (или среднеарифметическая) скорость молекул вычисляется в соответствии с правилом:

v = .

Распределение молекул по энергиям поступательного движения имеет вид:

()d = .

Распределение Больцмана. Если газ находится во внешнем силовом поле, то концентрация молекул зависит от координат. Из условия механического равновесия газа можно получить:

n( ) = n( ₀) exp ,

где  ( ) – потенциальная энергия молекулы во внешнем поле (распределение Больцмана). Частным случаем распределения Больцмана является барометрическая формула:

n(h) = n₀exp(- , p(h) = n(h)kT = p₀exp(- .

Распределение Максвелла-Больцмана. Распределение Максвелла и распределение Больцмана содержат выражение exp(- ). Распределение Максвелла-Больцмана выражает вероятность того, что произвольная молекула из объема содержащего N молекул, находится в области пространства (x, x + dx; y, y + dy; z, z + dz) и имеет скорость в интервале (v_x, v_x+ d v_x; v_y, v_y + dv_y; v_z, v_z + dv_z):

= dn( ) .

Здесь d³ = dxdydz, d³ = dv_xdv_ydv_z,  = +  ( ) – механическая энергия молекулы, А – коэффициент, который можно найти из условия нормировки. Общее распределение Максвелла-Больцмана применимо к любым видам энергии молекулы: энергии вращения, энергии колебаний, потенциальной энергии, зависящей от ориентации молекул, и так далее.