
- •Часть 1
- •О главление
- •Предисловие
- •После изучения дисциплины необходимо знать
- •После изучения дисциплины необходимо уметь
- •Содержание дисциплины
- •Самостоятельная работа студентов и контроль знаний студентов
- •После изучения главы необходимо знать
- •Простейшие интегралы
- •После изучения главы необходимо знать
- •2 Рис. 2.1 Рис. 2.1 .1. Кинематика материальной точки
- •Примеры решения задач
- •2.2. Кинематика абсолютно твердого тела
- •Примеры решения задач
- •2.3. Динамика материальной точки
- •Примеры решения задач
- •2.4. Законы сохранения
- •Примеры решения задач
- •2.5. Динамика абсолютно твердого тела
- •Примеры решения задач
- •2.6. Механика деформируемых тел
- •2.7. Механика жидкостей и газов
- •М етоды определения вязкости.
- •2.8. Неинерциальные системы отсчета
- •Пример решения задачи
- •2.9. Специальная теория относительности
- •Примеры решения задач
- •После изучения главы необходимо знать
- •3.1. Гармонические колебания
- •3.2. Свободные незатухающие механические колебания
- •С другой стороны, при малых углах
- •3.3. Затухающие механические колебания
- •3.4. Вынужденные механические колебания. Резонанс
- •3.5. Упругие волны
- •После изучения главы необходимо знать
- •4.1. Основные положения и определения
- •4.2. Уравнение состояния идеального газа
- •4.3. Внутренняя энергия и теплоемкость идеального газа
- •4.4. Кинетическая теория идеального газа
- •4.5. Реальные газы
- •Вопросы для самоконтроля к разделу 1: Элементы векторного анализа
- •К разделу 2: Физические основы механики
- •К разделу 3: Колебания и волны
- •К разделу 4: Молекулярная физика и термодинамика
- •Т олковый словарь
- •Инертность тел – свойство, присущее всем телам и заключающееся в том, что тела оказывают сопротивление изменению их скорости (как по модулю, так и по направлению).
- •Кинематика – раздел механики, изучающий движение тел без рассмотрения причин, которые это движение обуславливают.
- •З аключение
- •Б иблиографический список
- •Краткий курс физики
- •Часть 1
- •394026 Воронеж, Московский просп.,14
Простейшие интегралы
|
|
|
|
|
|
|
|
2 ГЛАВА |
|
||
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ |
|
||
|
2.1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ |
|
|
|
2.2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА |
|
|
|
2.3. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ |
|
|
|
2.4. ЗАКОНЫ СОХРАНЕНИЯ |
|
|
|
2.5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА |
|
|
|
2.6. МЕХАНИКА ДЕФОРМИРУЕМЫХ ТЕЛ |
|
|
|
2.7. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ |
|
|
|
2.8. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА |
|
|
|
2.9. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ |
|
|
Физика – это точная естественная наука, изучающая наиболее общие формы движения материи (вещества и поля) и их взаимные превращения. Движение является неотъемлемым свойством материи и формой ее существования. Изучаемые физикой формы движения: механическая, молекулярная, тепловая, электромагнитная, атомная, ядерная присутствуют во всех более сложных формах движения материи.
Изучением механической формы движения занимается раздел физики – механика; ее составными частями являются: кинематика, динамика, статика. Под механическим движением понимается изменение положение тела или его частей относительно других тел в пространстве с течением времени.
В классической (ньютоновской) механике изучается механическое движение макроскопических тел, происходящее со скоростью, много меньшей скорости света в вакууме. В релятивистской механике (специальной теории относительности) изучается механическое движение макроскопических тел при скоростях, близких к скорости света. В квантовой механике изучается механическое движение микроскопических тел (атомов, элементарных частиц).

Цель главы – изучить основы классической кинематики и динамики материальной точки и тела, законы сохранения, элементы механики жидкостей, газов и твердых тел, неинерциальные системы отсчета, некоторые вопросы теории относительности.
После изучения главы необходимо знать
Основные понятия кинематики; уравнения, описывающие механическое движение.
Законы динамики и силы в механике.
Законы сохранения.
Элементы механики твердого тела.
Элементы механики жидкостей, газов.
Неинерциальные системы отсчета.
Основы специальной теории относительности.
2 Рис. 2.1 Рис. 2.1 .1. Кинематика материальной точки
Кинематика занимается описанием механического движения тел без выяснения причин, его вызывающих. Телом называется макросистема молекул (атомов), размеры которой намного больше межмолекулярных (межатомных) расстояний. Системой тел является мысленно выделенная совокупность тел.
Д
Рис. 2.2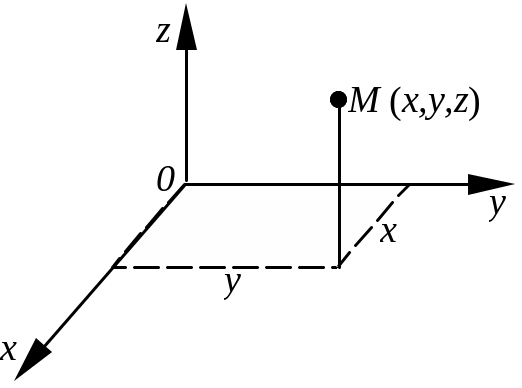
В физике используются различные системы координат. Простейшей системой координат является прямоугольная декартова система, в которой положение точки задается как М (x, y, z) (рис. 2.1).
Положение точки М (ρ, φ, z) в цилиндрической системе (рис. 2.2) задается длиной ρ отрезка ОМ′ , соединяющего начало координат О с проекцией М′ (x, y, O) точки М на плоскость xOy, углом φ между осью х и отрезком ОМ′ и координатой z точки М. Цилиндрические координаты ρ, φ, z связаны с декартовыми координатами следующими соотношениями:
2
=
x2
+ y2,
φ
= arctg
![]() и x
= ρcosφ,
y
= ρsinφ,
z
= z.
и x
= ρcosφ,
y
= ρsinφ,
z
= z.
В
Рис. 2.3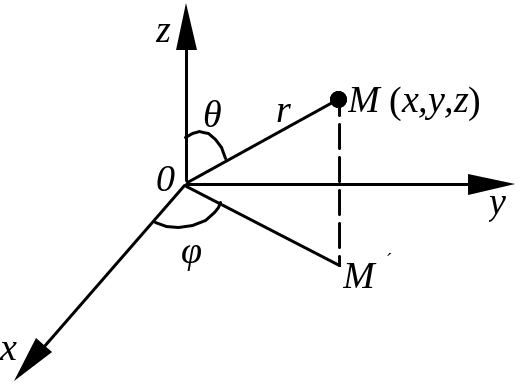
r²
= x2
+ y2
+ z2,
φ
= arctg
![]() ,
θ
= arctg
,
θ
= arctg
![]()
и
x = rsinθcos φ, y = rsinθsinφ, z = rcosθ.
Существуют
различные способы описания движения
точки. При координатном
способе
задания положения точки, например в
декартовой системе координат, движение
материальной точки М
определяется тремя функциями, выражающими
зависимость координат от времени: x
= x(t),
y
= (t),
z
= z
(t).
Эта зависимость координат от времени
называется законом
движения
(или уравнением движения). При векторном
способе
положение точки М
в пространстве определяется в любой
момент времени радиусом-вектором
![]() =
(t),
проведенным из начала координат до
точки (рис. 1.7). При заданной
траектории L
движения точки М
ее положение относительно начала
отсчета О можно определить с помощью
криволинейной
координаты
l
(t)
(рис. 2.4).
=
(t),
проведенным из начала координат до
точки (рис. 1.7). При заданной
траектории L
движения точки М
ее положение относительно начала
отсчета О можно определить с помощью
криволинейной
координаты
l
(t)
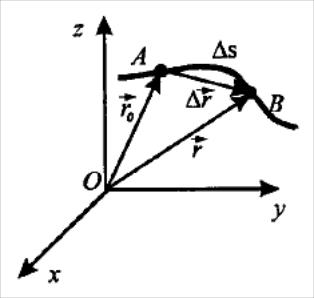
(рис. 2.4).
К
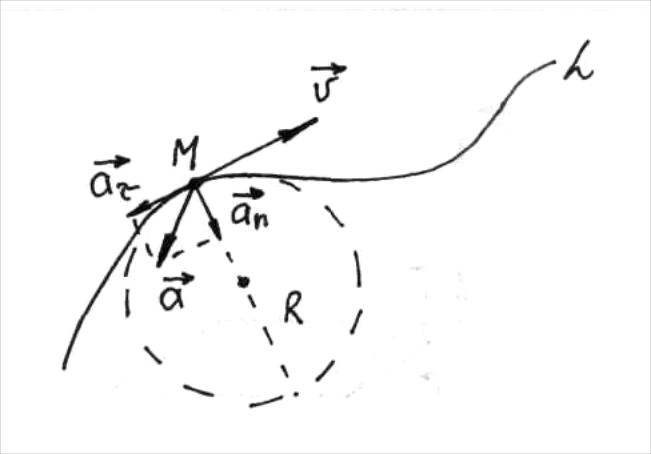
М
Рис.2.5![]() .
Мгновенная скорость направлена по
касательной к траектории .
.
Мгновенная скорость направлена по
касательной к траектории .
Средняя скорость за конечное время Δt есть векторная величина, определяемая как отношение перемещения Δ к интервалу времени Δt и совпадающая по направлению с вектором Δ :
ср
=
![]()
С
Рис. 2.6
v
=
![]()
Мгновенное
ускорение
векторная величина, характеризующая
быстроту изменения скорости и равная
первой производной вектора скорости
или второй производной радиуса-вектора
по времени:
![]() .
Направление вектора ускорения составляет
с вектором скорости некоторый угол α,
изменяющийся в пределах 0 ≤ α
≤ π.
Ускорение лежит в той же плоскости, что
и участок траектории. Проекцию ускорения
на направление скорости называют
тангенциальным
ускорением
и обозначают
.
Направление вектора ускорения составляет
с вектором скорости некоторый угол α,
изменяющийся в пределах 0 ≤ α
≤ π.
Ускорение лежит в той же плоскости, что
и участок траектории. Проекцию ускорения
на направление скорости называют
тангенциальным
ускорением
и обозначают
![]() .
.
Тангенциальное
ускорение определяет быстроту изменения
скорости по величине
![]() =
=
![]() и направлено по касательной к траектории.
Другую компоненту ускорения,
перпендикулярную скорости, называют
нормальным
ускорением
(рис. 2.6) и обозначают
и направлено по касательной к траектории.
Другую компоненту ускорения,
перпендикулярную скорости, называют
нормальным
ускорением
(рис. 2.6) и обозначают
![]() .
Нормальное ускорение характеризует
быстроту изменения направления скорости
и равно
=
.
Нормальное ускорение характеризует
быстроту изменения направления скорости
и равно
=
![]() ,
где R
– радиус кривизны траектории, то есть
радиус окружности, наиболее близко
примыкающей к траектории в данной точке,
–
нормальный вектор. Вектор
направлен
по радиусу кривизны R
к центру соответствующей окружности.
,
где R
– радиус кривизны траектории, то есть
радиус окружности, наиболее близко
примыкающей к траектории в данной точке,
–
нормальный вектор. Вектор
направлен
по радиусу кривизны R
к центру соответствующей окружности.
В
Рис. 2.7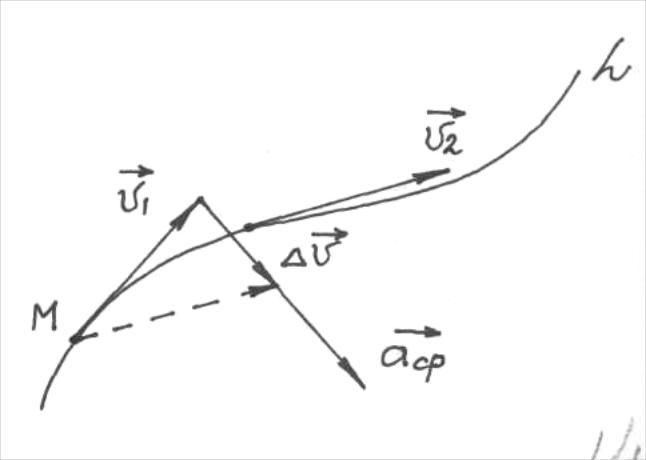
Модуль вектора ускорения равен:
a2
=
|
|2
+
|
|2
= (![]() .
.
Среднее
ускорение за интервал времени Δt
определяется как
![]() =
=
![]() (рис. 2.7).
(рис. 2.7).
Виды движения. Характеристика движения по известному закону (уравнению) движения называется прямой задачей кинематики, при решении которой находятся основные кинематические величины точки. Задачу определения уравнения движения точки по известным основным кинематическим величинам, однозначно заданным начальными условиями, называют обратной задачей кинематики. Решение обеих задач в общем виде возможно с помощью дифференциального и интегрального исчисления. Для некоторых простых частных случаев движения задача может быть решена с применением методов элементарной математики. Во многих случаях задача кинематики не сводится ни к прямой, ни к обратной. В этом случае для определения закона движения приходится решать дифференциальное уравнение.
В зависимости от формы траектории выделяются следующие виды движения точки: прямолинейное и криволинейное, а в зависимости от ускорения виды движения точки характеризуются как равномерное (движение с постоянной скоростью), равнопеременное (равноускоренное или равнозамедленное) и переменное (ускорение меняется со временем):
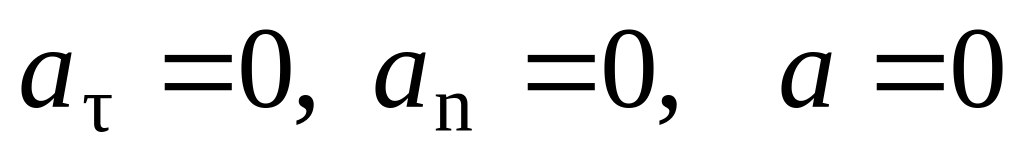 ,
— прямолинейное равномерное движение.
,
— прямолинейное равномерное движение.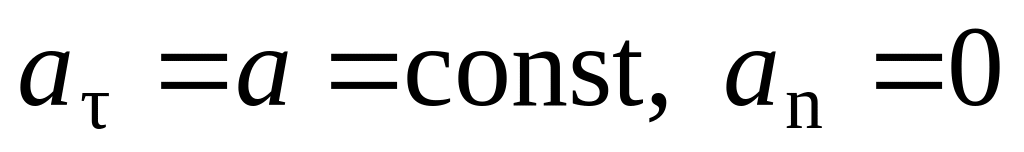 — прямолинейное
равноускоренное движение. Если t0
= 0, то
— прямолинейное
равноускоренное движение. Если t0
= 0, то
Рис.
2.8![]()
![]()
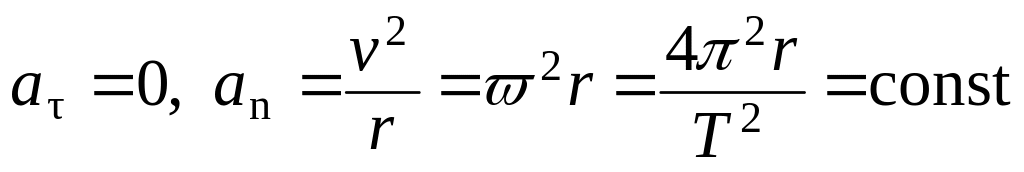 -
равномерное движение по
окружности.
-
равномерное движение по
окружности.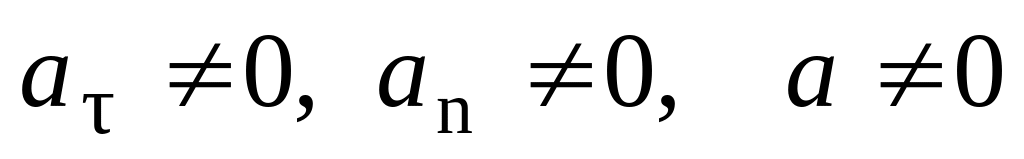 —
криволинейное
равнопеременное движение.
—
криволинейное
равнопеременное движение.
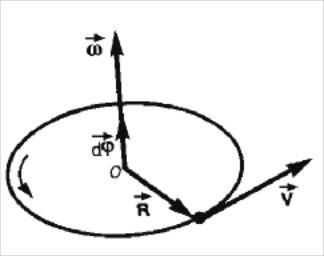
Движение материальной точки по окружности. Движение по окружности (вращение) является частным случаем криволинейного движения, при котором радиус кривизны R траектории (окружности) остается постоянным. Движение точки М по окружности можно описать с помощью угловых переменных (рис. 2.8):
угла
поворота
dφ,
который определяется как угол, на который
поворачивается радиус-вектор точки,
длина которого равна радиусу|
|
= R,
проведенному из центра окружности |
|
= R.
Малый угол поворота, или угловое
перемещение, можно рассматривать как
псевдовектор
![]() ,
направленный по оси вращения по правилу
правого винта;
,
направленный по оси вращения по правилу
правого винта;
угловой
скорости
![]() =
=
![]() псевдовекторной величины, характеризующей
быстроту вращения и направленной вдоль
оси вращения по правилу правого винта;
псевдовекторной величины, характеризующей
быстроту вращения и направленной вдоль
оси вращения по правилу правого винта;
углового
ускорения
![]() =
=
![]() псевдовекторной величины, определяющей
быстроту изменения угловой скорости и
направленной так же вдоль оси вращения.
При ускоренном вращении вектор
совпадает по направлению с вектором
псевдовекторной величины, определяющей
быстроту изменения угловой скорости и
направленной так же вдоль оси вращения.
При ускоренном вращении вектор
совпадает по направлению с вектором
![]() ,
при замедленном вращении вектор
противоположно
направлен вектору
.
,
при замедленном вращении вектор
противоположно
направлен вектору
.
Если
угол поворота dφ
за время dt
измерять в радианах, то длина дуги равна
ds
= Rdφ.
Отсюда следует, что линейная скорость
движения точки по окружности (R
= const)
равна по величине v
=
![]() = Rω,
а величины тангенциального и нормального
ускорений равны, соответственно:
= Rω,
а величины тангенциального и нормального
ускорений равны, соответственно:
=
![]() = εR
и
=
= εR
и
=
![]() = ω2R.
= ω2R.
В случае равномерного движения по окружности нормальное ускорение иногда называют центростремительным.
Формулы
для нормального и тангенциального
ускорений можно вывести, если записать
скорость в виде
=
v![]() ,
где
– единичный
вектор, направленный вдоль скорости.
Получим
=
+
v
,
где
– единичный
вектор, направленный вдоль скорости.
Получим
=
+
v![]() и учтем, что
и учтем, что
![]() =
=
=
=
![]() ,
где
– единичный
вектор, перпендикулярный к скорости
и
направленный вдоль радиуса. Этот вывод
справедлив и для произвольной
траектории, если принять соотношение
d
=
,
где
– единичный
вектор, перпендикулярный к скорости
и
направленный вдоль радиуса. Этот вывод
справедлив и для произвольной
траектории, если принять соотношение
d
=
![]() за определение как направления нормали
,
так и радиуса кривизны R.
за определение как направления нормали
,
так и радиуса кривизны R.
Кинематические величины, имеющие одинаковые значения в разных системах отсчета, называют инвариантными.
Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Относительными кинематическими величинами точки являются координаты, перемещение, скорость, ускорение.
Если движение
точки рассматривается из двух систем
отсчета К и К′, оси которых
остаются все время параллельными друг
другу, то между скоростями точки
и
![]() относительно этих систем отсчета в
каждый момент времени выполняется закон
сложения скоростей
относительно этих систем отсчета в
каждый момент времени выполняется закон
сложения скоростей
=![]() +
+![]() ,
,
где – скорость системы К′ относительно системы К и значения скоростей много меньше скорости света в вакууме. Такое же соотношение выполняется и для ускорений:
=
+
![]() .
.

