3.5. Упругие волны

Упругой волной называется процесс распространения механических колебаний в упругой сплошной среде, содержащей атомы и молекулы, когда происходит нарушение их устойчивого равновесия в одном месте (источнике), приводящее к распространению возмущения с определенной скоростью.

Упругая волна может распространяться в трехмерной среде, двухмерной среде (упругая мембрана), одномерной среде (упругий стержень, натянутая жеская нить, столб воздуха).

Волновое движение среды описывают функцией  ( , t), задающей смещение частицы среды от равновесного положения в момент времени t.

Простейший вид волны – плоская волна, в которой функция  =  (х, t) меняется только в одном направлении и зависит от координаты х. Если при этом вектор  перпендикулярен направлению распространения волны, то волна называется поперечной, а если параллелен – продольной.

Среда называется однородной, если все ее точки эквивалентны, изотропной, если в ней равноправны все направления, упругой, если возникающие силы зависят только от смещения (деформации), линейной, если силы пропорциональны деформациям. В абсолютно упругой среде механическая энергия волны не рассеивается (не превращается во внутреннюю). Если среда обладает только объемной упругостью, то в ней могут распространяться только продольные волны (жидкость, газ), если она обладает также упругостью формы, то возможны и поперечные (сдвиговые) волны. В линейной среде распространение волн описывается линейными дифференциальными уравнениями, и осуществляется принцип суперпозиции: если два независимых источника вызывают две разных волны ₁( , t) и ₂( , t), то совместное действие источников вызовет волну  ( , t) = ₁ ( , t) + ₂ ( , t). Такое же утверждение верно и для одного источника, движение которого можно разложить на два движения. Поскольку любою функцию времени можно представить в виде интеграла Фурье по гармоническим функциям, то волновое движение линейной среды можно разложить на гармонические волны. Через произвольную точку гармонической волны можно провести единственную поверхность постоянной фазы, которая называется волновой поверхностью. Волновая поверхность, совпадающая с передним краем волнового возмущения, называется фронтом волны.

Уравнение плоской гармонической волны. Если в источнике смещение происходит по закону (0, t) = mcos(t), то в точках с координатой х смещение происходит по такому же закону, но с запаздыванием на , где v – скорость распространения волны (бегущей волны):

(х, t) = _mcos( ) = _mcos( t - х) = _mcos(t – kх),

где  = = vT – длина волны, k = = - волновое число.

Длина волны представляет собой кратчайшее расстояние между точками, совершаюшими синхронные колебания (разность фаз ∆φ = 2) (рис. 3.9). Разность фаз между произвольными точками волны равна

∆

Рис. 3.9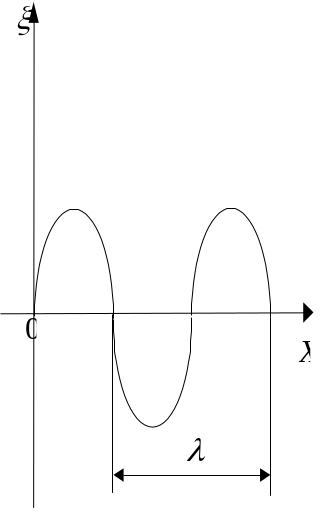

φ = .

Если ввести волновой вектор , направленный перпендикулярно фронту волны в сторону ее распространения, то уравнение бегущей волны принимает вид, инвариантный по отношению к выбору системы координат:

 ( , t) = _mcos(t – ).

Если скорость волны не зависит от частоты (отсутствует дисперсия), то плоское волновое возмущение распространяется без искажения формы. При распространении волны от точечного (сферического) или линейного (цилиндрического) источника изотропно по всем направлениям волновые поверхности будут иметь соответственно форму сфер или круговых цилиндров. Бегущая волна переносит энергию. Если предположить, что потери энергии на расстоянии х от источника возмущения пренебрежимо малы, то по закону сохранения энергии поток переносимой энергии будет оставаться постоянным. Убывание же амплитуды колебаний происходит вследствие возрастания площади волновой поверхности.

Волновое уравнение. Непосредственной подстановкой можно убедиться, что смещение гармонической волны  ( , t) удовлетворяет уравнению

+ + = , или ∆  = ,

которое называется волновым уравнением. При отсутствии дисперсии такому же уравнению удовлетворяет любая суперпозиция плоских волн. Если уравнение движения частицы среды приводится к подобному волновому уравнению, то волновое возмущение данной среды распространяется со скоростью v.

В одномерном случае общее решение волнового уравнения имеет вид

 = ₁ +  ₂ = f₁(x – vt) + f₂(x + vt),

где f₁ и f₂ – произвольные дифференцируемые функции. Первое слагаемое ₁ описывает распространение плоского сигнала f₁(x) со скоростью v без изменения формы в направлении положительных х, а второе слагаемое ₂ – распространение сигнала f₂(x) со скоростью v в направлении отрицательных х.

Энергия бегущей волны. Для бегущей волны произвольной формы  = f(x ± vt) выполняется соотношение = v² . Учитывая, что для упругой продольной волны v² = (Е – энергия волны, ρ – плотность среды), можно получить, что плотности кинетической энергии W_к = и потенциальной энергии W_п = в каждой точке бегущей волны равны друг другу. Это утверждение верно для бегущей волны любой природы. В случае гармонической плоской волны (х, t) = _mcos(t – kх) объемная энергия волны и ее среднее по времени значение имеют вид:

W = W_к + W_п = ρ²_m²sin²(t – kх) , w = ρ²_m² .

Плотность потока энергии (вектор Умова) в данной точке бегущей волны равна = u, где u – скорость переноса энергии. Для бездисперсионной среды u = v, где v – скорость распространения волны, входящая в волновое уравнение. Для гармонической бегущей волны u = v, где v = – фазовая скорость волны. Энергия, переносимая бегущей волной через площадку ds за единицу времени (поток энергии), равна d = d . Интенсивность гармонической плоской волны равна  = ρv²_m².

Стоячие волны. Две волны называются когерентными, если в любой точке пространства они создают колебания, разность фаз которых не меняется со временем. Источники когерентных волн называются когерентными источниками. При сложении некогерентных волн средняя по времени энергия результирующего колебания равна сумме их средних энергий. При сложении когерентных волн, колебания частиц в которых происходят в одном или близких направлениях, может наблюдаться явление интерференции (устойчивое во времени ослабление колебаний в одних точках пространства и усиление – в других). Если точка находится на расстоянии r₁ от одного из когерентных источников и на расстоянии r₂ – от другого, то разность фаз между колебаниями в этой точке равна

∆φ = (φ₁₀ - kr₁) - (φ₂₀ - kr₂ ) = - (φ₂₀ - φ₁₀) = 2( ) - ∆φ₀,

где ∆φ₀ – разность фаз между колебаниями источников, ∆ = (r₂ – r₁) – разность хода волн.

Условие максимума результирующих колебаний: ∆φ = ± 2m;

условие минимума: ∆φ = ± 2 ,

г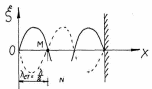 де m – порядок интерференционного максимума (минимума). В случае синфазных источников (∆φ₀ = 0) эти условия принимают вид:

∆ = ± m (максимум), ∆ = ± (m – ) (минимум).

В

Рис.3.10

ажным примером интерференции является стоячая волна, возникающая при сложении двух одинаковых плоских бегущих волн, распространяющихся навстречу друг другу и при этом уравнение стоячей волны записывается в виде:

 = _mcos(t – kх) + _mcos(t + kх) = 2_mcos(kх)cos(t).

Амплитуда колебаний точек волны А(х) = 2_mcos(kх) периодически меняется от нуля в узлах волны (точка М) до 2_m в пучностях волны (точка N) (рис. 3.10).

Расстояние между соседними узлами (пучностями) равно длине стоячей волны _ст = , где  - длина бегущей волны. Средняя по времени энергия имеет одинаковое значение во всех точках стоячей волны. Стоячая волна не переносит энергию. И бегущие и стоячие волны не переносят вещество.

4 ГЛАВА
	МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
		4.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ
		4.2. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
		4.3. ВНУТРЕННЯЯ ЭНЕРГИЯ И ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
		4.4. КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА
		4.5. РЕАЛЬНЫЕ ГАЗЫ

Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом, содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический.

Молекулярная физика изучает строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Термодинамика изучает свойства макроскопических систем и протекающие в них процессы, не вдаваясь в микроскопическую природу этих тел. Два этих направления взаимно дополняют друг друга.

Цель главы – изучить основные положения и законы молекулярно-кинетической теории и термодинамики, закономерности поведения идеальных и реальных газов, жидкостей, особенности строения твердых тел.