
- •Часть 1
- •О главление
- •Предисловие
- •После изучения дисциплины необходимо знать
- •После изучения дисциплины необходимо уметь
- •Содержание дисциплины
- •Самостоятельная работа студентов и контроль знаний студентов
- •После изучения главы необходимо знать
- •Простейшие интегралы
- •После изучения главы необходимо знать
- •2 Рис. 2.1 Рис. 2.1 .1. Кинематика материальной точки
- •Примеры решения задач
- •2.2. Кинематика абсолютно твердого тела
- •Примеры решения задач
- •2.3. Динамика материальной точки
- •Примеры решения задач
- •2.4. Законы сохранения
- •Примеры решения задач
- •2.5. Динамика абсолютно твердого тела
- •Примеры решения задач
- •2.6. Механика деформируемых тел
- •2.7. Механика жидкостей и газов
- •М етоды определения вязкости.
- •2.8. Неинерциальные системы отсчета
- •Пример решения задачи
- •2.9. Специальная теория относительности
- •Примеры решения задач
- •После изучения главы необходимо знать
- •3.1. Гармонические колебания
- •3.2. Свободные незатухающие механические колебания
- •С другой стороны, при малых углах
- •3.3. Затухающие механические колебания
- •3.4. Вынужденные механические колебания. Резонанс
- •3.5. Упругие волны
- •После изучения главы необходимо знать
- •4.1. Основные положения и определения
- •4.2. Уравнение состояния идеального газа
- •4.3. Внутренняя энергия и теплоемкость идеального газа
- •4.4. Кинетическая теория идеального газа
- •4.5. Реальные газы
- •Вопросы для самоконтроля к разделу 1: Элементы векторного анализа
- •К разделу 2: Физические основы механики
- •К разделу 3: Колебания и волны
- •К разделу 4: Молекулярная физика и термодинамика
- •Т олковый словарь
- •Инертность тел – свойство, присущее всем телам и заключающееся в том, что тела оказывают сопротивление изменению их скорости (как по модулю, так и по направлению).
- •Кинематика – раздел механики, изучающий движение тел без рассмотрения причин, которые это движение обуславливают.
- •З аключение
- •Б иблиографический список
- •Краткий курс физики
- •Часть 1
- •394026 Воронеж, Московский просп.,14
Примеры решения задач
Пример 1. К концу нити, намотанной на блок c моментом инерции I и радиусом R, привязали тело массой m и отпустили. Найдите ускорение тела.
Решение: Запишем
второй закон Ньютона для тела:
=
+
![]()
![]() ma = mg
– T, и уравнение
динамики вращающегося тела относительно
оси вращения z для блока:
ma = mg
– T, и уравнение
динамики вращающегося тела относительно
оси вращения z для блока:
![]() TR
= I.
TR
= I.
Так как нить по блоку не проскальзывает, то учтем также кинематическое соотношение а = R. Решая эти уравнения, получим
а =
 .
.
Пример 2. Найдите ускорение а круглого тела, которое скатывается без проскальзывания по плоскости, которая наклонена под углом .
Решение: Уравнение движения тела имеет вид: mgsin - Fтр = ma, где на основании уравнения динамики вращающегося тела FтрR = I. Условие отсутствия проскальзывания v =R приводит к уравнению а = R. Решая уравнения, находим ускорение:
а
=
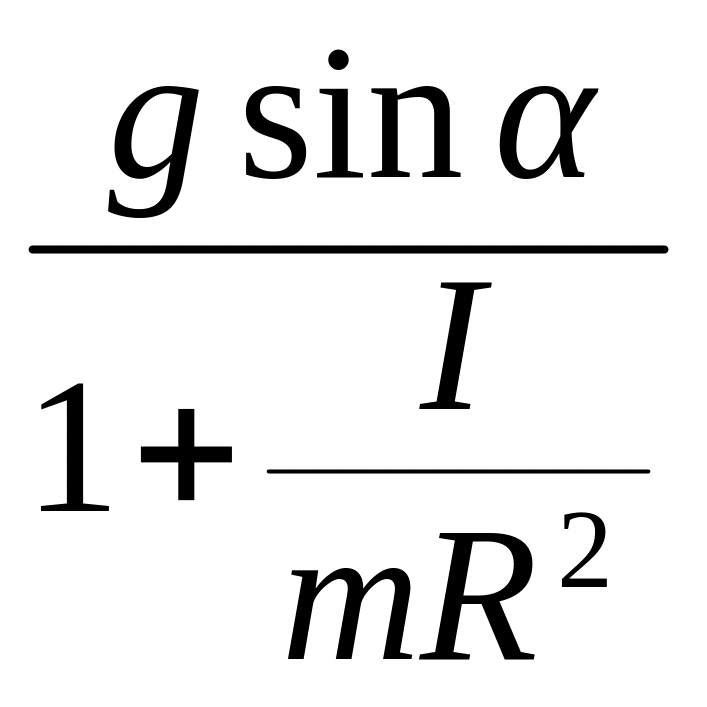 .
.
Так как сила трения работы не совершает, то механическая энергия сохраняется.
П
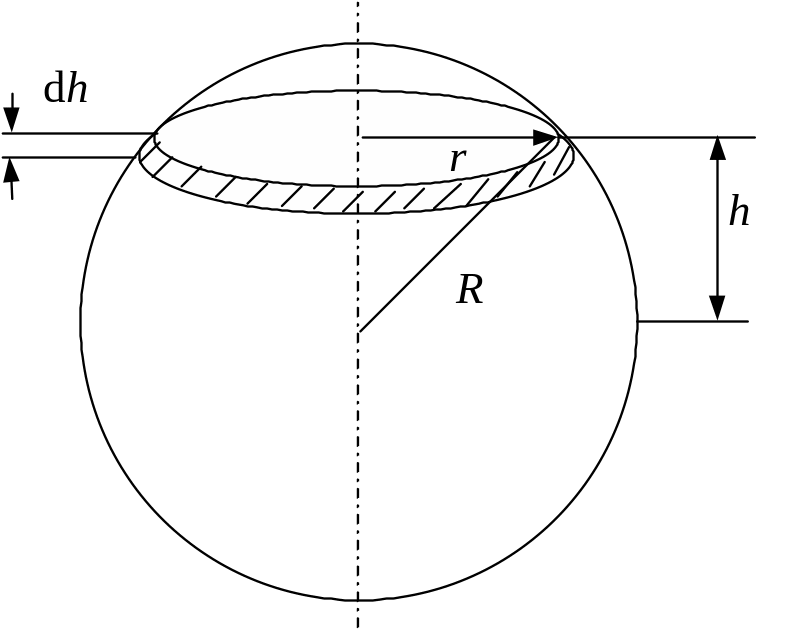 Рис.
2.19
Рис.
2.19
Решение:
Момент инерции слоя (диска):
![]()
![]()
![]()
С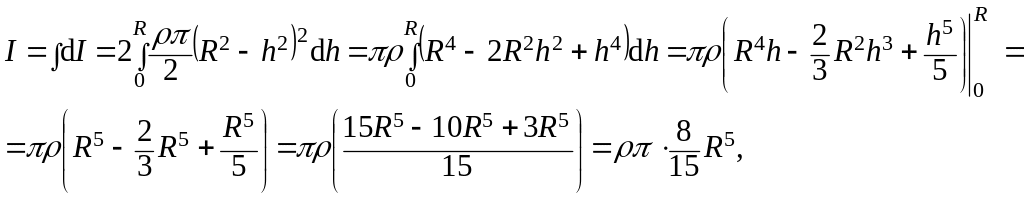 ледовательно:
ледовательно:
Масса шара:
![]()
![]()
П
Рис.
2.20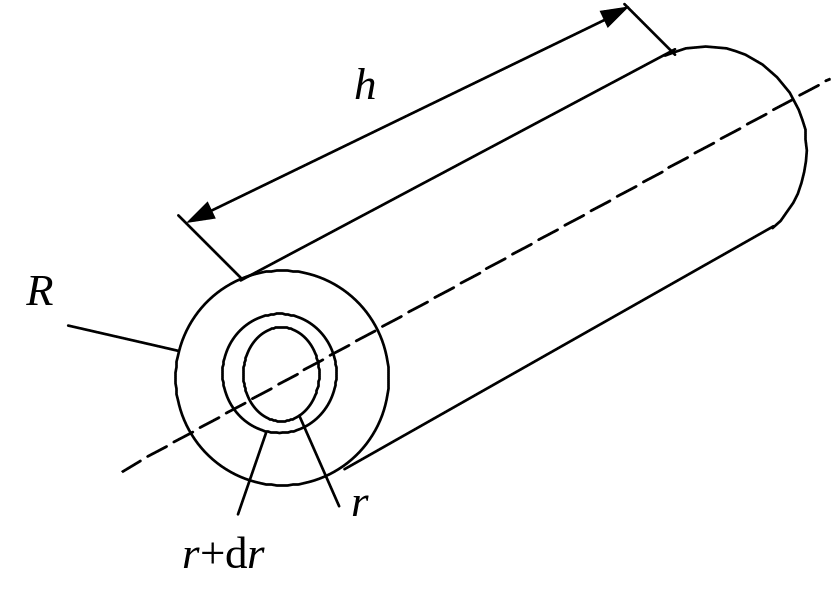
Решение:![]()
Разобьем цилиндр радиуса R на концентрические слои толщиной dr . Пусть радиус какого-то слоя r, тогда масса частиц, заключенных в этом слое, будет:
![]()
Представим, что весь цилиндр разбит на такие слои; тогда момент инерции всего цилиндра будет равен сумме бесконечно малых моментов или момент инерции всего цилиндра:
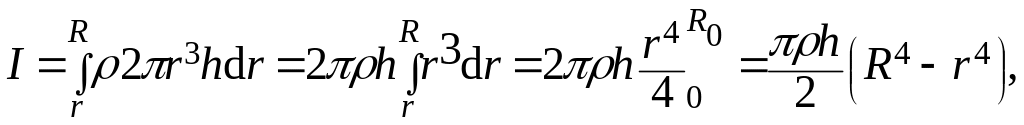

![]()
![]()
2.6. Механика деформируемых тел
Всякое тело под действием приложенных к нему сил деформируется в реальных условиях сложным образом. Однако любую сложную деформацию при определенных ограничениях можно свести к более простым деформациям. Основными видами простых деформаций являются: продольное (одностороннее или одноосное) растяжение (сжатие), сдвиг, кручение.
Продольное растяжение (сжатие). Деформация продольного растяжения (сжатия) сопровождается увеличением (уменьшением) длины L тела, например, однородного стержня (рис. 2.21), под действием растягивающей (сжимающей) силы n.
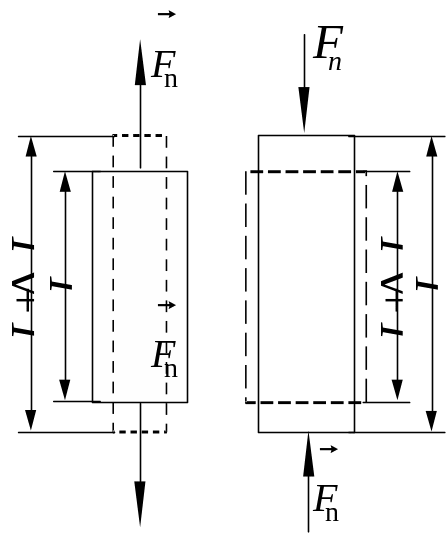 Рис.
2.21
Рис.
2.21![]() упруго деформированного стержня прямо
пропорциональна значению относительной
деформации ε
=
упруго деформированного стержня прямо
пропорциональна значению относительной
деформации ε
=
![]() ,
где ∆L
– абсолютная деформация (абсолютное
изменение длины), L
–
длина недеформированного стержня, Fn
– величина нормальной деформирующей
силы, S
– площадь поперечного сечения стержня:
,
где ∆L
– абсолютная деформация (абсолютное
изменение длины), L
–
длина недеформированного стержня, Fn
– величина нормальной деформирующей
силы, S
– площадь поперечного сечения стержня:
σn
=
![]() .
.
Величину
коэффициента пропорциональности Е
=
![]() ,
равную такому нормальному напряжению
σ
,
равную такому нормальному напряжению
σ![]() ,
при котором относительная деформация
стержня равнялась бы единице ε
= 1 (при этом стержень изменяет свои
размеры в два раза), называют модулем
Юнга.
Измеряется величина Е
в паскалях (Па). С введением модуля Юнга
закон Гука для стержня можно записать
в виде соотношения:
,
при котором относительная деформация
стержня равнялась бы единице ε
= 1 (при этом стержень изменяет свои
размеры в два раза), называют модулем
Юнга.
Измеряется величина Е
в паскалях (Па). С введением модуля Юнга
закон Гука для стержня можно записать
в виде соотношения:
Fn
=
![]() ∆L
= k
∆L,
∆L
= k
∆L,
где k – постоянный для данного стержня коэффициент упругости (закон выполняется до предела упругости тела).
Деформированное растяжением (сжатием) тело обладает запасом упругой энергии (потенциальной энергии), равной работе, затраченной на изменение размеров тела в процессе деформации:
Εупр
=
![]() Fn(x)dx
=
Fn(x)dx
=
![]() xdx
=
xdx
=
![]() ,
,
где V – объем тела. Объемная плотность упругой энергии (потенциальная энергия, приходящаяся на единицу объема деформированного тела) равна:
W
=
![]() =
=![]() =
=
![]() .
.
О
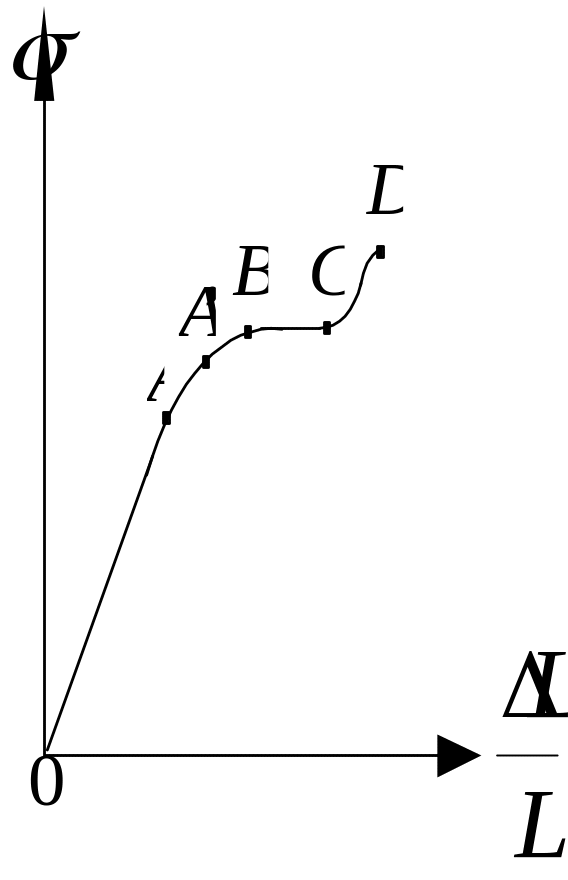 Рис.
2.22
Рис.
2.22![]() ,
где d
– поперечный размер тела. Коэффициентом
Пуассона
μ
называется отношение относительного
поперечного сужения (расширения)
к относительному продольному растяжению
(сжатию)
,
где d
– поперечный размер тела. Коэффициентом
Пуассона
μ
называется отношение относительного
поперечного сужения (расширения)
к относительному продольному растяжению
(сжатию)
![]() :
:
μ
=
![]()
П
Рис. 2.23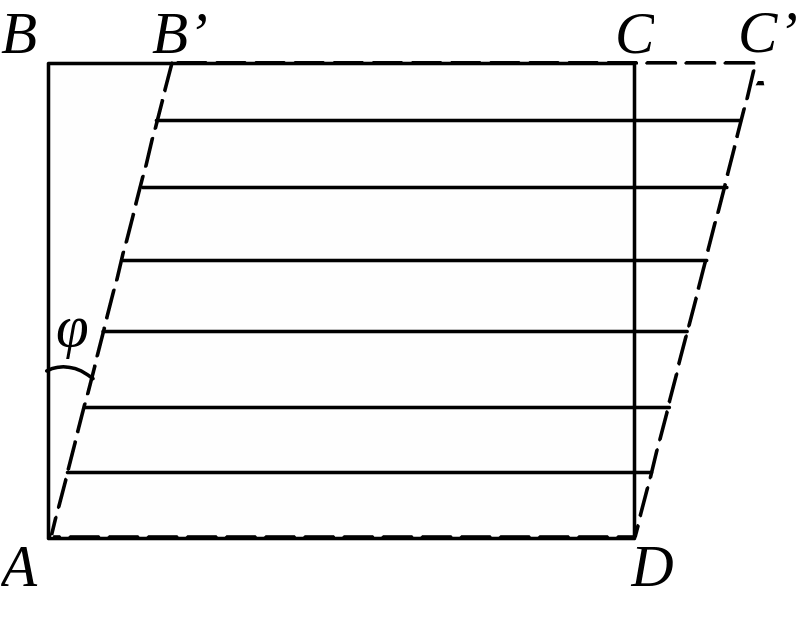
![]() начинает возрастать быстрее, чем
напряжение σ
(наблюдается отклонение от закона Гука).
Пределом
упругости
(точка А')
называется максимальное напряжение,
при котором еще не получаются остаточные
деформации.
Предел
текучести
(точка В)
характеризует состояние деформированного
тела, после которого удлинение возрастает
без увеличения деформирующей силы
(отрезок ВС).
Пределом
прочности
называется напряжение, соответствующее
наибольшей нагрузке, выдерживаемой
телом перед разрушением (точка D).
начинает возрастать быстрее, чем
напряжение σ
(наблюдается отклонение от закона Гука).
Пределом
упругости
(точка А')
называется максимальное напряжение,
при котором еще не получаются остаточные
деформации.
Предел
текучести
(точка В)
характеризует состояние деформированного
тела, после которого удлинение возрастает
без увеличения деформирующей силы
(отрезок ВС).
Пределом
прочности
называется напряжение, соответствующее
наибольшей нагрузке, выдерживаемой
телом перед разрушением (точка D).
Сдвиг
– деформация твердого тела, например,
имеющего форму прямоугольного
параллелепипеда АВСD
(рис. 2.23), при которой плоские слои тела,
параллельные плоскости
с
Рис.
2.24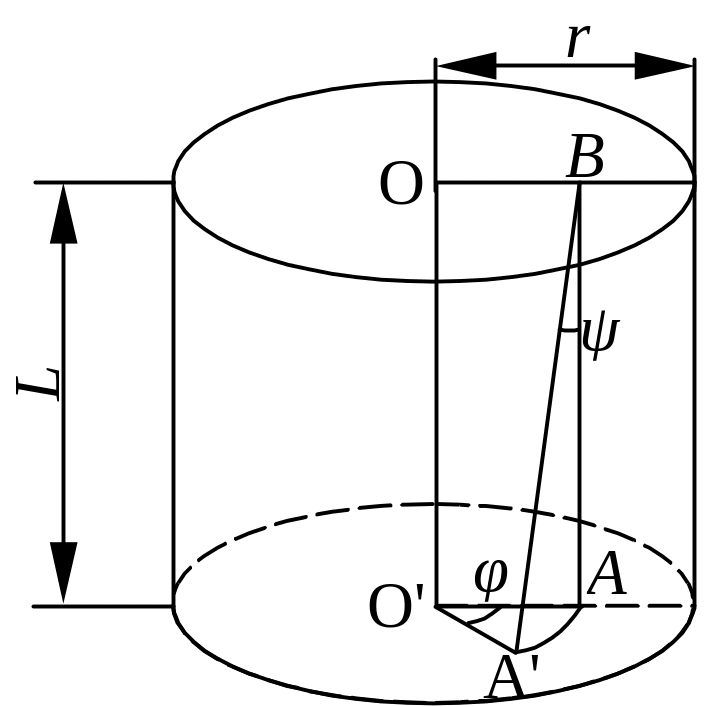
![]() ,
приложенной к грани ВС.
Противоположная грань АD
закреплена неподвижно (можно считать,
что на нее также действует касательная
сила
,
приложенной к грани ВС.
Противоположная грань АD
закреплена неподвижно (можно считать,
что на нее также действует касательная
сила
![]() ,
направленная противоположно силе
и
равная ей по величине
=
).
Под действием касательного напряжения,
величина которого равна σ
=
,
направленная противоположно силе
и
равная ей по величине
=
).
Под действием касательного напряжения,
величина которого равна σ
=
![]() ,
тело деформируется так, что грань ВС
сместится относительно грани АD
на некоторое расстояние ВВ'
= ∆x,
называемое абсолютным сдвигом. Если
тело однородное, то каждый элементарный
слой окажется сдвинутым относительно
соседних с ним слоев. При этом, любая
прямая, первоначально перпендикулярная
к слоям (например, грань АВ
= x),
повернется на некоторый угол φ.
В качестве характеристики деформации
сдвига берется величина
,
тело деформируется так, что грань ВС
сместится относительно грани АD
на некоторое расстояние ВВ'
= ∆x,
называемое абсолютным сдвигом. Если
тело однородное, то каждый элементарный
слой окажется сдвинутым относительно
соседних с ним слоев. При этом, любая
прямая, первоначально перпендикулярная
к слоям (например, грань АВ
= x),
повернется на некоторый угол φ.
В качестве характеристики деформации
сдвига берется величина
γ
=
![]() = tgφ
,
= tgφ
,
называемая относительным сдвигом. При упругих деформациях угол φ бывает очень мал. Поэтому можно считать, что tgφ ≈ φ. Следовательно, угол сдвига φ оказывается равным относительному сдвигу γ, для которого справедливо эмпирическое соотношение: Gγ = σ.
Величина G, называемая модулем сдвига, численно равна касательному напряжению σ, которое возникло бы в теле при относительном сдвиге равном единице γ = 1 (при этом угол сдвига оказался бы равным 45°, если бы не был превзойден предел упругости). Измеряется G, как и Е, в паскалях (Па).
Кручение – простой вид деформации, который сводится к деформации сдвига. Возьмем стержень в виде круглого цилиндра длиной L и радиуса r (рис. 2.24).
Пусть верхнее
сечение стержня закреплено неподвижно,
а к нижнему приложен момент силы
,
закручивающий стержень. Под влиянием
закручивающего момента отрезок О'А,
отложенный вдоль одного из радиусов
нижнего сечения, повернется на угол
закручивания φ и займет
положение О'А'. Относительной
деформацией кручения будет величина
![]() ,
пропорциональная закручивающему моменту
(в пределах упругой деформации) и равная:
,
пропорциональная закручивающему моменту
(в пределах упругой деформации) и равная:
![]() .
.
где
с – коэффициент пропорциональности,
постоянный для данного стержня, Ip
– полярный момент инерции сечения,
равный Ip![]() .
.
При кручении стержня его нижний торец испытывает сдвиг относительно верхнего, прямая ВА поворачивается и принимает положение ВА', угол ψ является углом сдвига. Связав деформацию кручения (угол кручения φ) с деформацией сдвига (угол сдвига ψ) и произведя математические преобразования, можно записать формулу для закручивающего момента:
![]() ,
,
откуда следует, что угол закручивания φ зависит от модуля сдвига G, обратно пропорционален радиусу стержня, взятому в четвертой степени, и прямо пропорционален длине стержня.
Величина
D,
называемая модулем
кручения,
показывает какой нужно приложить
крутящий момент
для
закручивания тела на угол φ
в один радиан. Измеряется D
в ньютонах на метр (![]() ).
).
Соотношения
между модулями упругости.
Деформация всестороннего растяжения
(сжатия) состоит в увеличении (уменьшении)
объема тела без изменения его формы под
влиянием равномерного распределения
деформирующих сил по всей поверхности
тела. По закону Гука напряжение σ
и относительное изменение объема
![]() тела связаны соотношением:
тела связаны соотношением:
σ = К ,
где К называется модулем всесторонней объемной упругости и имеет смысл напряжения, при котором относительное изменение объема равно единице
К
=![]() ,
,
где Е – модуль Юнга, μ – коэффициент Пуассона.
Модуль сдвига G связан с модулем Юнга Е и коэффициентом Пуассона соотношением:
G
=
![]()
![]() .
.
